Modulokat tartalmazó függvénygrafikonok létrehozására szolgáló módszerek
A lecke bemutatása
A lecke célja:- ismételje meg a modul jeleit tartalmazó funkció grafikonok létrehozását;
- hogy ismerkedjen meg egy új módszerrel egy lineáris darab funkció grafikonjának ábrázolásával;
- állítson be egy új módszert a problémák megoldására.
A bemutató 1. diaén.
Mi az y = | x | függvény grafikonja. (2-es dia).
(egy és két koordináta-szög sávtartománya)
Keresse meg a funkciók és a grafikonok közötti megfelelést, magyarázza el a választását (3. dia).
Diák: ehhez a funkcióhoz grafikont kell készíteni
- építsünk ki parabolát y = x 2 -2x-3
- az OX fölötti gráf egy része megmarad és az OX alatti grafikon egy része szimmetrikusan jelenik meg az OX tengely körül (5. dia)
Diák: Ehhez a funkcióhoz grafikát kell készíteni:
- a x 0 grafikonjának része tárolódik és a szimmetriák az OY tengelyhez viszonyítva jelennek meg (7. dia)
Diák: Ehhez a funkcióhoz grafikát kell készíteni:
- Szükséges egy y = x 2 -2x-3 parabola létrehozása
- Y = x 2 -2 | x | -3 -et építünk, a grafikon egy részét tároljuk, és szimmetrikusan leképezzük az OC
- az OX feletti rész megmarad és az alsó rész szimmetrikusan leképezve az OX-hoz viszonyítva (9. dia)
A következő feladat írásban történik írásban.
1. Plot a darabonkénti lineáris y = | x + 2 | + | x 1 | - | x 3 |
- a szubmodul kifejezéseinek zérusai x1 = -2, x2 = 1, x3 = 3
- szakítsa meg a tengelyt résekbe
- minden egyes intervallumnál írjuk le a függvényt
-2-nél<1, у=х
1-szer<3, у = 3х-2
- a lineáris darabot ábrázoljuk.
A moduldefinícióval (dia 10) funkcionális gráfot készítettünk.
Felhívom a figyelmedet a "csúcsmódosítási módszerre", amely lehetővé teszi a lineáris darab funkció grafikáját (11. dia). A gyermekek építésének algoritmusa jegyzetfüzet.
algoritmus:- Megtaláljuk az egyes modulok nulláit
- Olyan táblázatot állítunk össze, amelyben a nullák mellett az argumentum egyik értékét a bal oldalon és a jobb oldalon
- A pontokat a koordináta síkjára helyezzük és sorba kapcsoljuk
2. Vegyük ezt a módszert, hogy ugyanaz a funkció = | x + 2 | + | x-1 | - | x-3 |
A tanár a táblára van, a gyerekek a notebookban vannak.
- megtaláljuk az egyes modulok nulláit;
- összeállítunk egy táblázatot, amelyben a nullákon kívül az argumentum egyik értékét a bal és a jobb oldalon
- A pontokat a koordináta síkjára helyezzük és sorba kapcsoljuk.
A lineáris töredékfüggvény grafikonja egy törött vonal, végtelen extrém kapcsolatokkal (12. dia).
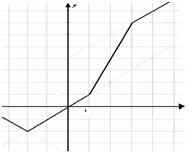
Hogyan gyorsul és könnyebb a grafikon?
3. A módszer rögzítéséhez a következő feladatot javasolom:
Melyik x értéke adja meg a y = | x-2 | - | x + 1 | függvényt a legnagyobb értéket veszi fel.
Követjük az algoritmust; tanuló a táblára.
y (3) = 1-4 = 3, egymás után összekapcsoljuk a pontokat.
4. További feladat
Mekkora értékei a || 4 + x | - | x-2 || = a egyenletnek két gyökere van.
a) Az X értékeinek értékei: y = | 2x + 3 | +3 | x-1 | - | x + 2 | a legkisebb értéket veszi fel.
b) Az y = || x-1 | -2 | -3 | függvény grafikonját össze kell állítani .