Geometriai optimalizálási problémák

A geometriában sok probléma létezik, amikor egy függvény legnagyobb vagy legkisebb értékét szeretné megtalálni. Funkcióként megfontolható egy alak kerületének vagy területe, vagy például egy test térfogata, és a függvény argumentuma az ábra vagy a test bármely paramétere, az oldal hossza, az oldalak közötti szög és így tovább. Miután elkészült a függvény, egy extrém értékkel rendelkező derivált segítségével meg kell vizsgálni. Emlékeztetni kell arra, hogy általában ilyen példákban a függvény véges időközönként létezik, amelyet a rendszer geometriája és a probléma állapota határoz meg.

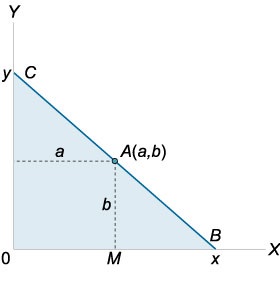
A koordinátarendszerben az első negyedévben beállított \ (A \ left (\ right). \) Végre sor ezen a ponton keresztül, egy cut-off háromszög legkisebb által határolt területen ez egyenes vonal és a koordináta-tengelyek (ábra \ (1 \)).

Tekintsük a háromszögeket \ (OBC \) és \ (MBA. \) Ezek a háromszögek hasonlóak. Következésképpen, a kapcsolat \ [\ frac >> = \ frac >> \; \; \ szöveg \; \; \ frac = \ frac>, \], ahol a koordináták \ (x \) és \ (y \) kielégíteni \ (\ x \\) \ [y = \ frac >>. \] A háromszög területét a következő függvény írja le \ (S \ bal (x \ jobbra): \) \ [.> = \ frac \ cdot \ frac >>> = >> \ right) >>> \] kiszámítja a-származék: \ [>> \ right) >>> \ right) ^ \ prime >> = >>>> \ right) ^ \ prime >> = \ cdot \ frac \ right) - >> \ right)> ^ 2 = >>>> \ cdot \ frac - 2ax - >> \ jobbra)> ^ 2 >>>> = \ right) >> \ right)> ^ 2 >>>.> \] függvény \ (S \ bal (x \ right) \) van kritikus pontok \ (x = 0, \) \ (x = a, \) \ (x = 2 \), mivel \ (x> a, \) a döntési pont \ (x = 2a. \) Amikor rajtuk átmenő a deriváltja elõjelet min sa plusz, azaz \ (x = 2a \) a függvény legkisebb pontja \ (S \ balra (x \ jobb) \)

Egy másik háromszög katétert számítunk ki: \ [\ require y = \ frac >> = \ frac >> = \ frac> = 2b. \] Így a legkisebb területű háromszögnek \ (2a \) és \ (2b. \)

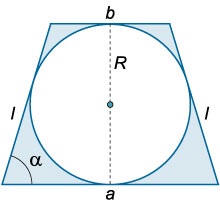
Az izosceles trapézis egy \ (R \) kör köré íródik (ábra \ (2 \)). Melyik szögben a \ (\ alpha \) alapja az árnyékos terület területe lesz a legkisebb?

Terület egyenlő szárú trapéz határozza \ [= \ frac> \ cdot h, \] ahol \ (a, b \) - bázis a trapéz, \ (h \) - a magassága. Nyilvánvaló, \ (h = 2R \.) Terület egy kör egyenlő \ (= \ pi \.) Ezután a terület az árnyékolt régió \ [- = \ frac> \ cdot 2R - \ pi> = \ right) R - \ pi. > \] Mivel a trapéz alakja körön belül van leírva, az ellenkező oldalak összege ugyanaz, pl. \ [\; \; >>>> =>.> \] Itt \ (\ ell \) jelöli a trapéz oldalát. Szubsztituálása \ (\ left (\ jobbra) \) az előző kapcsolatban, azt kapjuk: \ [>> \ cdot R - \ pi> = \ left (> - \ pi> \ right)> \.] Vizsgáljuk terület \ (S \ balra (\ alpha \ jobbra) \) szélsőséges értékre. Kiszámítjuk a származék \ (S „\ left (\ alpha \ jobbra): \) \ [\ left (> - \ pi> \ right)> \ right] ^ \ prime >> = \ left ( <- \frac^2>\ alpha >>> \ jobb) \ cdot \ cos \ alpha> = <- \frac\cos \alpha>> ^ 2> \ alpha >>.> \] Nyilvánvaló, hogy a származtatott egyenérték nulla a \ [\ cos \ alpha = 0, \; \; \ Rightarrow \ alpha = \ frac, \] ahol, amikor áthalad ezen a ponton (növekvő \ (\ alpha \)) származéka jel átvált mínusz plusz. Következésképpen \ (\ alpha = \ nagy \ frac \ normalsize \) - minimum pont \ (S \ left (\ alpha \ right) \.) Ebben az esetben a trapéz „fajul„a négyzeten. Az ábra területének legkisebb értékét a \ [> = \ left (\ right) képlet határozza meg. \]

Az ablak téglalap alakú, félkörrel határolva (ábra \ (3 \)). Az ablak kerülete \ (P. \) Határozza meg a \ (R, \) félkörív sugarát, amelyre az ablakterület a legnagyobb.

Nyilvánvaló, egyik oldalán a téglalap egyenlő \ (. 2R \) másik oldalán jelöljük \ (y \.) Kerülete az ablak által kifejezett \ [P = \ pi K + 2R + 2y \.] Ezért tapasztaljuk, hogy \ (y: \) \ [y = \ frac \ bal [

\ right]. \] Az ablak területe: \ [>> + 2Ry> = >> + 2R \ cdot \ frac \ left [

\ Right]> = >> + PR - \ pi - 2> = >> - 2> \] A kapott expressziós függvénye \ (. S \ left (r \ right) \), hogy vizsgálja a szélsőérték. Megtaláljuk a származékot: \ [>> - 2> \ right] ^ \ prime >> =

=

\] Adja meg a helyhez kötött pontokat: \ [\; \; \ jobb) R = 0,> \; \; >>> \] Mivel a második származék negatív: \ [\ right] R> \ right] ^ \ prime >> = <- \left( \right) r\)). Из данного бревна требуется вырезать балку в форме параллелепипеда с квадратным сечением наибольшего объема.

Feltételezzük, hogy a rúd tengelyei és a gerendák egybeesnek. A csonka kúp, és feltüntetik egy paralelepipedon ez vázlatosan mutatjuk ábra szerinti metszetben \ (14 \) határozza meg egy paralelepipedon térfogat \ [V = y, \] ahol \ (x \) - az alsó oldalon egy négyzet paralelepipedon, és \ (y \) - magassága.