Pont és intervallum becslések
Ha a paraméter becslés egy számot, egy ilyen értékelés hívják pont (egy pont a valós tengelyen). A fenti értékelés pontot.
Ha megtaláljuk az értéktartomány értékelésekor, hogy a valódi érték alá egy bizonyos valószínűsége annak, hogy egy ilyen értékelés lesz szakaszos. A megfelelő időközönként nazyvayutdoveritelnym intervallumban. és a valószínűsége -doveritelnoy valószínűsége (ilinadezhnostyu).
Tegyük fel például, x- átlagos diák pontszámot.
Példa pontbecslésének: = 4,5.
Példa intervallumbecslését: 4,2 ≤ ≤ 4,8 (vagy ezzel ekvivalens, = 4,5 ± 0,3) egy valószínűsége 0,93. Egy másik példa a intervallumbecslését: 4.1 4.9 ≤≤ valószínűséggel 0,95 (azaz = 4,5 ± 0,4).
Meg kell jegyezni, hogy minél nagyobb a bizalom szintjét vesszük, annál nagyobb a megbízhatósági intervallum. Tulajdonképpen a fenti példa ismerete nélkül is az értéke az átlag, akkor lehet mondani, hogy pontosan (1 valószínűséggel), hogy 2 ≤ ≤ 5, mint a többi értékek ebben értékelő skála venni általában nem. Ez az információ azonban nyilvánvalóan nem használ a kutató. Minél kisebb a megbízhatósági intervallum vesszük, annál nagyobb az esély a hiba, azaz a hogy nem fogjuk bejutni (és a megbízhatósági szint, illetve annál kevesebb). Ie pontosabb becsléseket kevésbé valószínű.
Így, ha a megbízhatósági határ bizonyos értékeit a paraméter egy képlet határozza meg A ± pri veroyatnosti bizalom, mi bolshe a bolshe. A opredeleniyaispolzuyutsya képletű, amelynek a formája attól függ, hogy melyik paramétert ítélik milyen módszerrel és milyen típusú mintát használunk a. Ezen kívül, ha ezt a képletet használjuk raschetepo információra mintanagyság és a lakosság és znachenii. Szükséges képletek találhatók tankönyvek és segédkönyvek a statisztika.
Tesztelés Statisztikai hipotézisek
Statisztikai hipotézis - nincs semmiféle utalás formájában, vagy az értékeket a paraméterek valószínűségi eloszlása.
Amikor ellenőrzi a statisztikai hipotézisek hipotézis, hogy az ellenőrzések általában nevezik a nullhipotézist és oboznachatHo. Egyidejűleg rassmatrivayutalternativnuyu (versengő) H1 hipotézist. GipotezyHo és N1 kell egymással szembeállítani.
Az elv a statisztikai hipotézis vizsgálatához a következő. Alapján a mintavételi adat kiszámítása egy alak , amely az úgynevezett a vizsgálati statisztika. Ez az arány egy valószínűségi változó (mert számítani a mintából), de ez úgy van megválasztva, hogy a valószínűség-eloszlása ismert (esetleg hozzávetőleges). Emellett znacheniedolzhno lehet az oka, vagy nem egy hipotézist kell vizsgálni. Minden lehetséges znacheniyarazbivayut két különálló domének egy domain-kilökődés ikriticheskuyu terület (amely elutasította a hipotézis). Például, a kiválasztott kritikus statisztika kriteriyakr olyan, hogy ha a hipotézis helyes, akkor annak a valószínűsége, hogy haladja meg ezt az értéket α α = P (> kr) nagyon kicsi (α = P (> kr)). Ezután pri≤kr hipotézist elfogadjuk, míg az összes többi znacheniyahotklonyaetsyaHo.
Jellemzően a szignifikancia vizsgálat az úgynevezett statisztikai kritériumnak.
Azonban a valószínűsége α még lehet hiba (azaz De a hipotézist elvetjük, holott igaz). Ez akkor fordulhat elő, mert az érték a statisztikai esik a kritikus terület véletlenül. Nazyvayutoshibkoy ez a hiba az első ilyen. és a megfelelő valószínűségi nazyvayuturovnem szignifikancia vizsgálat. Ez kicsinek kell lennie.
Továbbá azt is elismerte, mint egy hiba, a második fajta : ez abban a tényben rejlik, hogy gipotezaHo hozott, bár valójában ez a rossz (és valódi alternatívát gipotezaH1). Megjegyezzük, hogy a tesztelés során ugyanazt a hipotézist mintán, azonos mennyiségű ugyanakkor lehetetlen, hogy csökkentse a hibák előfordulásának valószínűsége az első és a második fajta. Ez annak a ténynek köszönhető, hogy a növekedés a kritikus területen, és egyidejűleg növeli α, i. Minél több kritikus terület, annál valószínűbb, hogy elutasítja a feltételezést, és kevésbé valószínű, hogy megkapja azt (vagy, ami valószínűbb, hogy elutasítja, vagy elfogadja bizonyos hamis). Valószínűleg nem véletlen, a második fajta nazyvaetsyamoschnostyu kritériuma (ez egyenlő 1 -).
Ugyanakkor növeli a teszt, és csökkenti a szignifikancia szintjét csak akkor lehetséges, növeli a minta mérete, mert csak ezen feltételek mellett, a minta érték mutatói pontosabban tükrözi majd az igazi megoszlásának jellemzőit, és annak a valószínűsége, véletlenszerű eltérések csökkentéséhez.
Például a raktár kapott termékek párt. Ebből a termékek egy részét az ellenőrzésre kiválasztott házasság. Az ellenőrzés lesz elfogadják vagy elutasítják a nullhipotézis, ami a következő: aránya a hibás elemeket a telek kicsi, és a párt is igénybe vehet. Tegyük fel először, hogy a kiválasztott termék frakció hibás volt nagy, és az eredményeket a mintavétel a teljes tételt utasítani. Ugyanakkor lehetőség van arra, hogy a vizsgáztató véletlenül kifogott egy rossz termék, és valójában a párt el kellett fogadnia, mert a többi termékek nem tartalmaznak házasság. Ebben az esetben az első fajta hiba történt, vagyis elutasította a nullhipotézist (elutasítására jó termék). Most tegyük fel, hogy az arány a hibás termékek kiválasztott kicsi volt, és az eredményeket a mintavétel fél vett. Ugyanakkor lehetőség van arra, hogy a vizsgáztató, hogy véletlenül hit a jó termék, és valójában a párt el kellett utasítani. Ebben az esetben a második fajta hiba történt, vagyis így egy rossz null hipotézist. Ezek a példák azt mutatják, hogy a további termékek kerülnek vizsgálatra kiválasztott, annál kisebb a kockázata, és az egyik és a másik hiba. Azonos minta térfogata a szigorúbb feltételek ellenőrzése (több kritikus terület), annál nagyobb a valószínűsége, hogy a hiba az első fajta és kisebb, mint - a második (és fordítva).
A yurispudentsii alatt a null hipotézist kifejezés általában azt a hipotézist, hogy a terhelt ártatlan. Ennek megfelelően, a hiba az első fajta - a vád egy ártatlan, és a hiba a második fajta - ez a kifogás a bűnös. alacsony szignifikancia szint hozzárendelés azt jelenti, hogy annak a valószínűsége, I-es típusú hiba kicsinek kell lennie, azaz a kockázata, hogy a rossz, „vádolni egy ártatlan ember” kicsinek kell lennie.
Attól függően, hogy a kritikus terület az űrlap valamennyi statisztikai teszteket lehet osztani három fő csoportba. Tekintsük a példát, ahol a képletben a statisztikát imeet standard normális eloszlás (t.e. = N (0, 1)), és adott öt százalék szignifikancia szint (α = 0,05):
1) a jobb kritikus régiót a következő egyenlőtlenség definiálja
Ha α = 0,05, akkor a terület alatt a grafikont a sűrűsége a standard normális eloszlás jobbra a sor x = kr kell lennie 0,05. A teljes terület alatt ez a grafikon jobb oldalán a függőleges tengely a 0.5. Ahhoz, hogy megtalálja znacheniekr. Az általunk használt Laplace funkciót, amely itt, hogy értéke 0,5-0,05 = 0,45. Az ilyen sootvetstvuetkr értéke = 1,64.
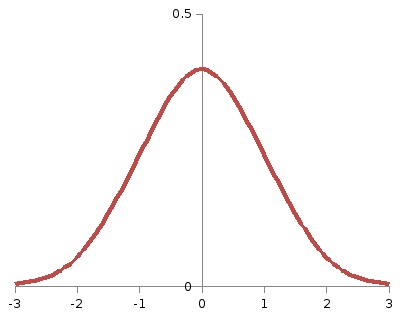
A 20. ábrán az árnyékolt terület a figura 0,05, azaz 5% -a az egységek (a teljes terület alatt a grafikont a sűrűségfüggvény). Ez azt jelenti, hogy a P (> kr) = α = 0,05. A legvalószínűbb elmélet vizsgálandó továbbra is elutasítják, ha ez tényleg igaz. Ha a tényleges érték kriteriya≤kr statisztika. A hipotézis.
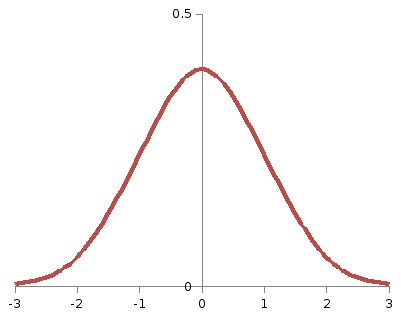
2) elhagyta a kritikus terület a következő egyenlőtlenség definiálja
Az ilyen érték megfelel kr = -1,64. A 21. ábra a vonalkázott területen is a szám 0,05, azaz P (<кр ) = α = 0,05. Если фактическое значение статистики критерия≥кр. гипотеза принимается.
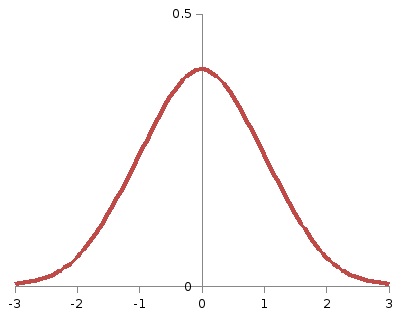
3) a két-utas kritikus régió által meghatározott egyenlőtlenségek
Mivel a terület a diagram alatt a sűrűség eloszlása a kritikus területen kell lennie 0,05, a terület minden egyes a két satírozott területek a 22. ábrán kell lennie 0,025 (azaz α / 2). Ezután a Laplace függvény az x = kr2 kell tennie a értéke 0,5-0,025 = 0,475. Az ilyen sootvetstvuetkr2 értéke = 1,96. Ennek megfelelően, kr1 = -1,96.
Tehát, ha kétoldalas tesztet P (<кр1 ) = = Р(>kr2) = α / 2. Eslikr1 ≤≤kr2. A hipotézis.
Tekintsük a következő példát. Csomagoló gép fűszerek szállítva úgy állítjuk be, hogy az átlagos súlya a fűszereket egy zsák egy teszt adag 50 darab volt, 90 = 0 (g) a SKOh = 10 (g). Egy hónap előrecsomagolt sarzsot kiválasztott táskák 60, és az átlagos súlya a fűszereket egy zsákban sostavila0 = 86 (g) SKOy = 8,5 (g). Meg kell kideríteni, hogy ez véletlen, vagy kiigazítás a gép elromlott.
Megfogalmazzuk a null hipotézis: a beállítás nem törött. Ez azt jelenti, hogy valójában az átlagos érték szállítás és abban a pillanatban egyenlő, azaz M (-) = M () - M () = 0. Tegyük fel, hogy a véletlenszerű változó, egy normális eloszlású 0.
Találunk az RMS e véletlen változó.
A variancia a valószínűségi változó? D () = D ((xi) / n)) = = (D (xi)) / 2 = (D (xi)) / n 2 = x 2 * n / n 2 = 2 x / n, ahol n = 50, t.e.D () = 100/50 = 2.
Hasonlóképpen, a D () = 2 y / n, ahol n = 60, t.e.D () = 8,5 2/60 = 72,25 / 601,2.
Ezután a D (-) = D () + D () = 3,2, és a SKO1,79.
Ezután statisztikák = (-) / 1,79 lesz egy standard normális eloszlás, t.e. = N (0, 1). Figyelembe mint az átlagos általános értékelési minta otsenki0 U0. Kiszámítjuk a tényleges érték a vizsgálati statisztika: = () / 1,792,23.
Tegyük fel szignifikanciaszint 5%. Készítünk egy kétoldalas kritikus régiót, ha a tényleges kritérium kerül, ez azt jelenti, hogy a különbség az átlagos túl szignifikánsan különbözik a nullától mindkét irányban; akkor azt a hipotézist, hogy az egyenlő eszközökkel kell utasítani. Laplace függvénytábla találjuk a határait ebben a régióban: F (kr2) = 0,5-0,05 / 2 = 0,475, togdakr2 = 1,96; kr1 = -1,96. Mivel 2,23> 1,96, a hipotézis H0 elutasítják, azaz beállítása a gép elromlott. Azonban van egy öt százalék a valószínűsége, hogy a levont következtetést véletlenül (azaz tulajdonképpen az autó minden rendben, csak egy rossz mintavétel történt).
Tegyük fel szignifikanciaszint 2%. Akkor azt találjuk, a kritikus terület az a Laplace függvénytábla a határ értékei ezt a funkciót (kr2) = 0,5-0,02 / 2 = 0,49, akkor togdakr2 = 2,34; kr1 = -2,34. Mivel 2,23> 2,34, el tudjuk fogadni a nullhipotézist szignifikancia szinten két százalék. Ie Feltételezzük, hogy a kiigazítás a gép nem sérült.