Esszé „titkait matematika”
A 3x3 bűvös négyzet magic constant 15 egyenlőnek kell lennie az összeg a három szám 8 irányban: 3 sor, 3 oszlop és 2 átlók. Mivel a szám a központban, tartozik egy sort, 1 oszlop, és az átlók 2, ez benne van 4 az 8 háromágyas, melyek összege magic constant. Ez a szám csak egy: ez 5. Ezért a számot a központ a bűvös négyzet 3x3 már ismert: ez egyenlő 5.
Tekintsük a szám 9. történik csak 2 háromágyas. Nem betette egy sarokban, mert minden sarkon cellához 3 háromágyas: sor, oszlop és átlós. Következésképpen, a 9-es szám kell lennie valamilyen ketrec szomszédos oldalán a tér a közepén. Mivel a szimmetria a tér nem számít, melyik oldalon úgy döntünk, ezért levelet 9 felett száma 5 állt a központi cellában. Mindkét oldalán kilences a felső sorban, csak akkor tudjuk meg a 2. és 4. Melyik ez a két szám jelenik meg a jobb felső sarokban, és ismét balra - nem számít, mint az egyik elrendezése számokat másik esetben a tükrös visszaverődés . A maradék sejteket automatikusan kitöltésre. Végeztünk egy egyszerű felépítésű, a bűvös négyzet 3x3 bizonyítja egyediségét.
Egy ilyen bűvös négyzet volt az ősi kínai szimbólum nagy jelentőséggel bír. 5. ábra jelentette a középutat, és szerte a láng (2 és 7) elrendezett szigorú egyensúlyt, vízzel (1 és 6), egy fa (3 és 8), fém (4 és 9).
A növekedés négyzet méretű (cellák száma) gyorsan nő a számos lehetséges mágikus négyzetek ilyen méretű. Ott 880 mágikus négyzetek annak érdekében, 4. és 275.305.224 mágikus négyzetek rend 5. Továbbá, 5x5 terek óta ismert a középkorban. Muszlimok, például nagyon tisztelettudóan kezeljük az ilyen téren az 1. számú középső, tekintve, hogy egy szimbólum egységének Allah.
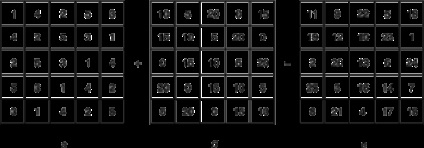
1.2.Magichesky tér - az ősi kínai eredetű. A legenda szerint uralkodása alatt császár Yu (c. 2200 BC), a Sárga-folyó víz (Sárga-folyó) alakult szent teknős shell, amelyen a titokzatos hieroglifák voltak írva (1A.), És ezek a jelek néven Lo Shu bűvös négyzet, és ekvivalens a ábrán látható. 1b. A 11. században. mágiáról négyzetek megtanulták Indiában, majd Japánban, ahol a 16. században. magic square kiterjedt irodalomban. Az európaiak be mágikus négyzetek a 15. században. Bizánci író E.Moskhopulos. Az első négyzet feltalált Európai tekinthető Durer square (ábra. 2) mutatja be a híres gravírozás melankólia 1. Alapítva metszetek (1514) tartalmaz, a számot a két központi sejtek az alsó sorban. Bűvös négyzetek különböző tulajdonított misztikus tulajdonságokkal. A 16. században. Cornelius Agrippa Heinrich épített terek 3., 4., 5., 6., 7., 8. és 9. megbízásokért járó asztrológia 7 bolygók. Gyakori hiedelem, hogy vésett ezüst bűvös négyzet véd pestis.

A 19. és 20. században. érdeklődés a bűvös négyzet tört újult erővel. Elkezdték vizsgálni módszerekkel algebra.

Csak normál magic square 3 × 3. Ismert volt az ókori Kínában, az első kép a teknős shell nyúlik vissza 2200 BC ..
Modern matematikusok hívja ezeket négyzetek „tökéletes”. Következésképpen a „tökéletes” és „ördögi” modern matematikusok - szinonimák!
De van egy másik MK nem kevésbé érdekes, mint az ördög. Kiváló amerikai szabadkőműves, tudós, közéleti és diplomata Benjamin Franklin volt egy négyzet 16 × 16, ami amellett, hogy a jelenléte állandó összeg 2056 az összes sorok, oszlopok és átlók van egy további tulajdonság. Ha vágott lap kockás papír 4 × 4 és helyezzük a lapot egy nagy tér, így a 16 négyzet alakú sejtek ebbe a nyílásba, a számok összege, amelyek megjelentek a nyílásba, nem számít, ha nem tesszük, nem lesz egy és ugyanaz - 2056.
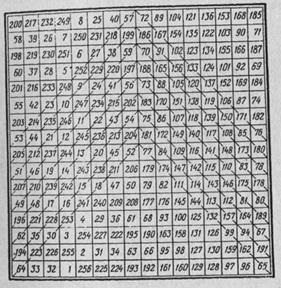
A tér a legtöbb mágikus mágikus összes MK húzott soha semmilyen bűvész.
1.4. Magic Quadrant Yang Hui (Kína). A 13. században. matematikus Yang Hui vette fel a problémát a módszerek építésének mágikus négyzetek. Kutatásai később folytatta a többi kínai matematikus. Yang Hui tekinthető mágikus négyzetek nem csak a harmadik, de nagy megrendeléseket. Néhány terek meglehetősen bonyolult, de mindig adta a szabályokat az építési. Volt képes kialakítani a bűvös négyzet a hatodrendű, az utóbbi majdnem asszociatív (csak két pár egymással szemben lévő központi számok nem adnak összesen 37):
Számok összege bármilyen vízszintes, függőleges és átlós egyenlő 34. Ez az összeg is megtalálható minden a négyzet sarkainak 2 × 2 egy központi tér (10 + 11 + 6 + 7), a tér a sarok sejtek (16 + 13 + 4 + 1 ) a négyzetek épített "swing ló" (2 + 8 + 9 + 15 és a 3 + 5 + 12 + 14), a téglalapok által alkotott pár szekunder cellák ellentétes oldalain (3 + 2 + 15 + 14 és 5 + 8 + 9 + 12). A legtöbb kiegészítő szimmetriák kapcsolódó tény, hogy az összeg a bármely két központilag szimmetrikus elrendezésű szám egyenlő 17.
1.5. Négyzetek Henry E. Dudeney és Allan W. Johnson ml.
Ha egy négyzetes mátrix n × n van rögzítve nem szigorúan természetes számok, akkor a mágikus négyzet - nem konvencionális. Az alábbiakban két ilyen mágikus négyzetek töltött többnyire prímszám. Az első a rend n = 3 (Dudeney négyzet); második (méret 4x4) - Johnson téren. Mindkettőt alakult ki a huszadik század elején:
Számos ilyen példát:
Az utolsó téren, 1913-ban épült Dzh.N.Mansi, figyelemre méltó, hogy ez áll a 143 egymást követő prímszám, kivéve két dolgot: a résztvevő egység, ami nem prímszám, és nem csak használják páros prímszám 2.
1917-ben, a francia-német front, NCO Franz Buhl, folytató fosztogatás a csatatéren talált a zsebében egy hindu katona hosszú csík vastag papír megölöttjei, melyet festett négyzetes cellákra osztjuk töltött arab írást. Átadta szalagban német professzor, aki részt vett a mágikus négyzetek. Valószínűleg a szalag tartalmazott egy talizmán, nem menti el, de a tulajdonos a haláltól.
Miután a fordítás arab, világossá vált, hogy a dokumentum tartalmaz egy bűvös négyzet a harmadik rend és a tér semimagic negyedik sorrendben. A 4 × 4 négyzete az ismétlések számát, és az összeg az átlók nem esik egybe az állandó:
Ezt követte egy listát a varázslatokat, nevét istenek és démonok, amelyben a professzor egyszerűen elszakadt és meg kell semmisíteni.
GlavaII. alapvető terminológia
Minden eleme a bűvös négyzet van a cella. Tér, az oldalán, amely áll N sejtek, amely 2 n sejtek és az úgynevezett négyzet a N-edik érdekében.
A legtöbb mágikus négyzetek használnak első n egymást követő egész szám. Sum S számok minden sorban és minden oszlopban sem a diagonális négyzet nevezzük állandó és egyenlő az S = n (n 2 + 1) / 2. Ezt bizonyítja, hogy n ≥ 3. függése a négyzetével érdekében vezethető segítségével az asztalra.
Két átlós áthaladó a tér közepén, az úgynevezett fő átló.
Bent úgynevezett átlós, amely, mielőtt elérik a szélén egy négyzet, párhuzamosan húzódik az első szegmens a szemközti élen (alkotnak egy átlós sötétített cellák ábrán.
Sejtek, amelyek szimmetrikusak az a tér közepén, az úgynevezett ferde. Ilyenek, például sejtek a és b.

GlavaIII. Módszerek töltési mágikus négyzetek

Páratlan érdekében mágikus négyzetek lehet kialakítani módszerével francia geométert 17. A. de la Luber (sziámiak módszer). Tekintsük ezt a módszert, mint például négyzetes rend 5 (ábra. 4). Az 1-es szám kerül a főtér a felső sor. Minden természetes számok találhatók a természetes rend ciklus alulról felfelé a sejtekben átlós jobbról balra. Miután elérte a felső szélén egy négyzet, folyamatos, hogy töltse ki az átlós, kezdve az alján a következő oszlop a sejtek (egy törött átlós). Miután elérte a jobb szélén a tér, továbbra is töltse ki az átlós, majd a bal oldali sejtvonal felett. Elérése a megtöltött ketrec vagy szögben, az út le az egyik cella lefelé, majd a töltési folyamat folytatódik.
Ahhoz, hogy a feltöltés egy négyzet ezzel a módszerrel, nevezetesen a helyének meghatározására a töltés a következő cella, miután egy négyzet élei használhatja a következő séma
1 szállítani átlagos cella-a felső sorban, és továbbra is a szekvenciát átlósan jobb felfelé. Ha a következő számot az átlós határán túl a tér, cseréljük ki a megfelelő mezőt a téren.
Tanulmányozva különböző forrásokból, felhívtuk a figyelmet arra a tényre, hogy lehetséges, hogy töltse ki a terek és a másik irányba, és nem feltétlenül érdemes 1 ebben a helyzetben.
3.2. Módszer F. De la Il (1640-1718) alapul két kezdeti négyzetek. Ábra. 5 megmutatja, hogyan kell használni ezt a módszert az építési tér érdekében 5. Az első cella egy négyzet illeszkedésének 1-5 úgy, hogy az ismétlések számát a sejtekben 3 fő átlósan elhelyezkedő a jobb felső, és nem talált számot kétszer egy sorban vagy egy oszlop. Ugyanez végzünk a számokat 0, 5, 10, 15, 20, az egyetlen különbség az, hogy a 10-es számú most ismétlődik a sejtek a főátlójában megy felülről lefelé (ábra. 5b). Teljes-sejt összege két négyzet (ábra. 5, c) képez mágikus négyzet. Ezt a módszert alkalmazzák az építőiparban négyzetének még sorrendben.
Elemzését követően a rendszer a kitöltési rajz, jöttem a következő algoritmust.
1. Az első helyen a négyzet számok 1-től N (a sorrendben a négyzet), úgy, hogy a másodlagos diagonális Állandó közepén eleme ezt a szekvenciát.
2. Az összes többi elem párhuzamosan vannak elrendezve, hogy az átlós törött átlók. Elements lejtős átló egyenlő.
3. A második helyen a négyzeten egymást követő többszörösei egy négyzet érdekében, kezdve 0 (az elemek száma egyenlő a sorrendben egy négyzet) úgy, hogy a fő diagonális Állandó közepén eleme ezt a szekvenciát.
4. Az összes többi elem párhuzamosan vannak elrendezve, hogy az átlós törött átlók. Elements lejtős átló egyenlő.
2.3. Extension szimmetrikus
sebesség gyémánt alakú

Lépésben kapott 1. ábra megtöltött sorok ferdén alulról felfelé - a megfelelő egész szám 1-ről 2 n szekvenciálisan. Kitöltése bemutatott eredményeket az alábbi ábra:
4. fejezet történő megtöltésére szolgáló eljárások mágikus négyzetek
érdekében négy többszöröse
Univerzális módszerek a bűvös négyzetek önkényes még rend még nem ismert. Ugyanakkor az egyes megközelítések kifejlesztett különféle különleges alkalmakra. Az alábbiakban a elkészítésének módját mágikus négyzetek, a sorrendben 4 többszöröse Ez a módszer kényelmes, hogy úgy a példa a bűvös négyzet a rend 8. A természetes számok 1-től 64. Az eljárás magában foglalja a következő lépéseket.
A tér festett két színben, és megtöltjük - track elrendezés egymást követő számok 1, 2, 3, 4, 5.
1. A kezdeti négyzet van osztva egy megfelelő számú négyzetek rend 4. Ebben az esetben, ezek a négyzetek lesznek 4. Az egyes al átlós elemek színes (fő és másodlagos).
2. A megmaradt elemek töltik soronként sorrendi egész számok balról és a felső -napravo fel- gombok valamelyikét a megtöltött -nalevo sejtek és jobbra és alulról felfelé nem töltött sejtek.
3. Az átmenet a színek között, amikor a feltöltés akkor jelentkezik, ha a következő, hogy töltse ki a cella színe megváltozik

5. fejezet alkalmazása mágikus négyzetek.
A hagyományos körét MC talizmánok. (Teljes lista bolygó talizmánok megtalálható a cikkely A.Sanarova „mágikus talizmánok. Gyakorlati útmutató”).
Például a Hold kabala bizonyos tulajdonságai: véd a hajótörés és a betegség, ami egy ember kedves, hozzájárul a megelőzés a rossz szándék, valamint javítja az egészséget. Ez van gravírozva az ezüst a napot és az órát a Hold, amikor a Nap vagy Hold az első tíz fok Rák. Bűvös négyzet 9. érdekében illeszkedik kilencszög (9 - Hold száma, lásd alább.), Körülötte pedig speciális karaktereket.
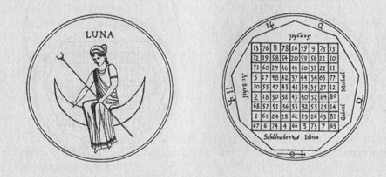
Vannak azonban olyan mágikus négyzet elemeire és jelei az állatöv. Keresse meg a megfelelő sorrendben a bűvös négyzet lesz Liber 777 Aleister Crowley, amely meghatározza a következő lehetséges:
Tárgy Matematikai terek - az egyik a hagyományos szakaszok szórakoztató matematika, amely a kíváncsi olvasó, mint a szép design és a súlyos megoldatlan problémák.
A dolgozatban tárgyalja kapcsolatos kérdéseket a történelem fejlődésének egyik kérdés a matematika, hogy elfoglalja a fejében a sok nagy ember - mágikus négyzetek. Annak ellenére, hogy a tényleges mágikus négyzetek nincsenek széles körben használják a tudomány és a technológia, a rendszer kéri, hogy a matematika osztályok sok kivételes ember, és hozzájárult ahhoz, hogy a fejlesztési más szakaszainak a matematika (csoport elmélet, determinánsok, mátrixok, stb.)
Tettem az alábbi következtetéseket:
1. Nincs sok töltésére alkalmas eljárásra mágikus négyzetek
2. A méretének növekedése a tér is gyorsan nő a számos lehetséges mágikus négyzetek. Például körülbelül 3 - csak 4-880 5 - közel negyed millió.
Nehéz megérteni, klasszikus zenei előkészítés nélkül. Nem könnyű észrevenni az absztrakt festészet, fogalma sincs, hogy a törvényeket. Ugyanez mondható el a számszerű mintákat.
Csodálatos, igazán varázslatos szépsége foglalt a bűvös négyzet, vonzza a legjobb elmék az emberiség évezredeken át. Értsd meg, nem mindenki megkap, de ha egyszer rájött a harmónia és a könyörtelen szigor a számok, kötött zsinór mágia, akkor kap nagy öröm.
Használja internetes források és szakirodalom
1. El Ignatiev "A királyság szellemes," M. "Nauka" 1979.
2. IY Depman, NY Vilenkin. Az oldalakon a matematika tankönyv.
3. Moszkva. Education. 1989.
5. Postnikov M. M. "Bűvös négyzetek" - M. Science 1964
7. kollégiumi szótár fiatal matematikus. M. "Pedagógia" 1989.
Tettem fel a feladatot „Bűvös négyzetek” az a döntés egy speciális kurzus a matematika.


Probléma 3. Rendezzük 16 betű
A tér, amely 16 sejtek pontozás
16 betűk (betűk 4 a, 4 betű b, 4 betű c, 4 betű d)
úgy, hogy minden vízszintes és függőleges sorban, minden levél csak egyszer fordulhat elő.
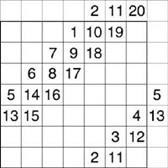
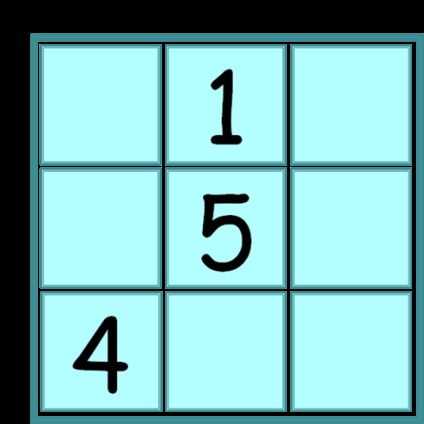
4. feladat gondoskodjon szám 9
A téren álló 9 sejt, 1,2,3,4,5,6,7,8,9 pontozás számát úgy, hogy a számok összege minden egyes függőleges, vízszintes sorban, és bármely átlós egyenlő.