Néhány számítógépes jellemző a
A közvetlen módszerek néhány képletet használnak az ismeretlen mennyiségek kiszámításához a számítási folyamat véges számú lépéseiben
Egy példa. Az inverz mátrix módszer
A közvetlen módszerek jelentős hiányossága az, hogy a rendszer mátrixának minden n-négyzet elemét meg kell őrizni a számítógép memóriájába, azaz a közvetlen módszerek semmilyen módon nem veszik figyelembe a mátrix lemerült struktúráját a rendszerekben.
Ezen túlmenően a közvetlen módszerek alkalmazása az SLAE megoldásához nagyszámú változóval jelentős számítási hibák felhalmozódását eredményezi.
A széles körben ismert módszerek közé tartozik a Gauss-módszer, a sweep módszer.
Iteratív módszerek (az egymást követő közelítések módszerei) olyan módszerek, amelyekben megközelítő megoldások láncolatát egy algoritmussal
Az ilyen számítások mindegyik ciklusát iterációnak nevezzük.
Az iteratív algoritmusok sokkal bonyolultabbak, mint a közvetlen módszerek. Az igénybevételhez szükséges számítások összegét nehéz előre meghatározni, de nem szükséges az összes elem tárolása a lemerült mátrixokkal való munka során. Ráadásul gyakran használják azokat a számítási képleteket, amelyek ezeket a példákat állítják. Az iteratív folyamat úgy van felépítve, hogy az iterációtól az iterációig terjedő számítási hibák ne halmozódjanak fel. Ezért az iteratív módszer használható mind a jól kondicionált, mind a rosszul kondicionált SLAU megoldására.
Példák: Az egyszerű iterációs módszer és a Gauss-Seidel módszer
Gauss-eliminációs módszer
Köztudott, hogy a Gauss-eljárás algoritmusa az SLAE megoldására két fő lépésből áll.
A rendszer egyenleteiből a változók egymás utáni eltávolításával az egyenes úton a rendszer mátrixa háromszög alakú.
az oldat eliminációs módszerrel felső háromszög mátrixot eredményez:
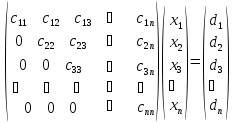
Fordított irányban a rendszer pontos megoldása
helyettesíti az előző egyenletet és kap:
A Gauss-módszer csak akkor hatásos, ha a rendszer mátrixa jól kondicionált, alacsony a feltételesség.
A számítás pontossága jelentősen függ attól, hogy az általunk használt vezető elemet használjuk a változók kizárására az előremenő mozgásban.
Egy példa. Tekintsük a rendszert:
Vegyük a vezető elemet
A döntésben megkapjuk:
ha lekerekítettek, akkor kb.
Vegyük a legfontosabb elemként az együtthatókat a második egyenletből, azaz 1.
Ezután, ha lekerekítettük, megkapjuk a helyes megoldást
A vezető kiválasztásának szabályai:
oszlop kiválasztása
Az első oszlopot figyelembe vesszük. Feltételezzük, hogy kizárunk. Ebben az oszlopban találjuk a maximális elemet, azaz a maximális elemet. Megtaláljuk azt az egyenletet, ahol az együttható nagy, és ezt az egyenletet átrendezzük az első helyre, és az együtthatót használjuk vezető elemként.
sorválasztás
Az első egyenletből egy változót találunk, amelyet kizárunk. Ennek megfelelően keressük és keresjük, ami megfelel ennek a maximális elemnek. És helyezze el az első helyet, és zárja ki.
Ez a technika minden elemre általánosítható
az egész mátrixban
Szkennelünk az oszlopokat és sorokat, és keressük őket. Ezt az elemet megtaláljuk és helyezzük először.
Ez a módszer elfogadható.
A sweep módszer a Gauss-eljárás speciális esete, amelyet kifejezetten az egyenletrendszerek megoldására terveztek hígított átlós mátrixszal
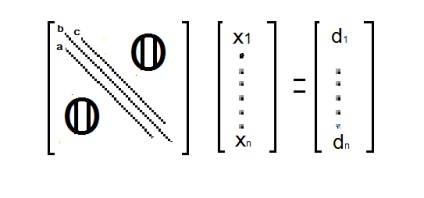
Az egyszerű tanfolyam az, hogy az együtthatók
A folyamat maga a következő.
A fordított futtatás megfelel a fordított sorrendben a változók kiszámításának, a legutóbbi x értékkel kezdődően
tudván, megtalálja
Általában az SLAU megoldására szolgáló iteratív módszerek rendszere a következő:
más módon meg kell határozni egy kezdeti megoldást
számítsd ki a jobb oldalt:
megtaláljuk az egyenletek rendszerének megoldását :, - a korrekciók vektora
az 5. tételtől a 2. pontig.
Fontos kérdés, hogy mikor kell megállni!
Állj le, használj minden olyan vektoregyenlőtlenséget, amely összehasonlítja az előző és utána következő iterációval kapott megoldásokat.