A mértéke a csúcspont (gráfelmélet)

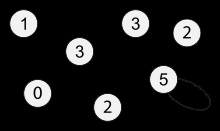
Ábra. 1. szám, melynek tetején jelzett mértékben.

A mértéke a vertex (Engl mértékben, ahogy vegyértékei Engl vegyérték ....) gráfelmélet - az élek száma a gráf incidens a vertex x. Kiszámításakor a fokú él-hurok kétszer számolni. [1] A mértéke vertex nevezik d (x) (a nyugati forrásokból - deg ⁡ (v)). Maximális és minimális mértékű a gráf G jelöli Δ (G) és a δ (G). Ábra. 1, a maximális mértéke 5, a legkisebb - 0. A rendszeres oszlopban fok minden csúcs azonos, így ebben az esetben beszélhetünk, milyen mértékben a grafikonon.

Kézfogás lemma

A képlet szerint az összege hatásköre a gráf G = (V E),

vagyis az összeg a fok a csúcsok egy gráf kétszeresével egyenlő számú szélétől. Ezen túlmenően, a képlet kell, bármilyen gráf a csúcsok száma a páratlan fokú is. Ez a kijelentés (és a formula is) ismert kézfogást Lemma. A név abból a jól ismert matematikai probléma: meg kell bizonyítani, hogy bármely csoport az embereknek a száma, hogy kezet páratlan számú egyéb, sőt.

A szekvenciát a vertex fok

Ábra. 2. Két izomorf gráf egyenlő mértékű szekvencia (3, 2, 2, 2, 2, 1, 1, 1).

A szekvenciát a vertex fok irányítatlan gráf egy nem-növekvő sorrendben. [2] A grafikon ábrán látható. 1, ez (5, 3, 3, 2, 2, 1, 0). A szekvenciát a vertex fok a grafikon van egy invariáns. így ez ugyanaz izomorf gráfok. Azonban a sorozat csúcs fok nem egyedi Környezeti adatok száma: bizonyos esetekben nem izomorf gráfok is ugyanabban a sorrendben.

Probléma fok szekvenciák, hogy néhány vagy az összes számít az előre meghatározott, nem-növekvő szekvenciából álló természetes számok (nulla fokos így figyelmen kívül lehet hagyni, mivel azok mennyisége megváltozik hozzáadásával vagy eltávolításával izolált csúcsok). A szekvencia egy szekvenciáját fokú grafikon nevezzük grafikai (Eng. Grafikus szekvencia). Formula összege hatásköre következik, hogy bármilyen sorrendben a páratlan összeget (például, 3, 3, 1) nem lehet szekvencia gráf fok. A fordítottja is igaz: ha a szekvencia chotnuyu összeget, ez egy szekvencia multigráf fok. Épület egy ilyen grafikon végezzük egyszerű módon: meg kell kombinálni a vertex páratlan hatáskörét párban. A fennmaradó betöltetlen tetejét ki kell egészíteni a hurok.

Nehezebb, hogy végre egy egyszerű gráf egy előre meghatározott sorrendben. Tétel Erdos - Gallai állítja, hogy a növekvő szekvencia di (ha i = 1, ..., n) lehet egy olyan szekvencia egyszerű gráf, ha annak mennyisége is és az egyenlőtlenség

Például, a szekvencia (3, 3, 3, 1) nem lehet egy sorozata egyszerű gráf; megfelel Erdos - Gallai csak akkor, ha k értéke 1, 2 vagy 4, de ha k értéke nem egyenlő 3.

Kritériumai szerint azokat a Havel-Hakimi [3]. ha egy nem-növekvő sorozat (d1 d2 ..., dn ..) egy sorozata, egyszerű gráf fok, a (d2 - 1, d3 - 1, ..., DD1 +1 - .. 1, DD1 +2 DD1 +3 ..., dn) egy olyan szekvenciát fokú egyszerű gráf. Ez a tény lehetővé teszi számunkra, hogy állítson össze egy polinomiális algoritmus megtalálása egyszerű gráf egy előre meghatározott sorrendben hajtják végre.

Mi társítja az eredeti sorszámok csúcsok nélkül bordák kívánt fok. Ez a transzformáció definiálja a szekvencia legalább egyik csúcsa a grafikon, minden él esetet, és több csúcsú új kiegészítéseket szükséges fok. Azáltal, hogy a maradék csúcsok a nem-növekvő kiegészítések fok érdekében, hogy nem-növekvő sorozat egyszerű gráf fok. Megismételve az átalakulás és ésszerűsítése nem több, mint n-1 alkalommal, megkapjuk a teljes grafikon.

A probléma a megállapítás a száma grafikonok vagy értékelési tárgya transzferázok egy előre meghatározott szekvencia grafikonok.

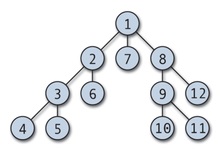
Ábra. 3. A terminális csomópontok 4, 5, 6, 7, 10, 11 és 12.

• Vertex fokú 0 nevezzük izolált.
• 1 nevezzük a mértéke a csúcs vége (Engl. Végén vertex), a lógó (Engl. Pendant vertex) vagy lap gráf (Engl. Levél vertex). Él az eset, hogy egy csúcsa az úgynevezett függő (Eng. Terminal (medál) él, végéi). Ábra. 3. lóg borda. Ezt a terminológiát a tanulmányban használt fák általában és adatstruktúrákat.
• A tetején a foka n-1 A grafikon az úgynevezett domináns érdekében n (Engl. Domináns vertex).

• Ha minden csúcsának ugyanolyan k. A grafikon az úgynevezett k-reguláris vagy szabályos grafikon fokú k. Ebben az esetben a gróf maga is egy k.
• Euler-kör létezik egy irányítatlan, összefüggő gráf, ha, és csak akkor, ha a gráf 0 vagy 2 csúcsok páratlan fokú. Ha a gráf tartalmaz vertex 0 páratlan fokú, Euler-kör egy ciklus.
• A kétjegyű mássalhangzó van psevdolesom [ismeretlen kifejezés] csak akkor, ha minden csúcs outdegree nem nagyobb, mint 1. A függvény grafikonján - psevdolesa speciális eset, amelyben az összes outdegree csúcsok értéke 1.
• Tétel szerint Brooks kromatikus száma grafikonon vagy klikk kivéve furcsa ciklus nem haladja meg a legnagyobb mértékben a csúcsok (Δ). Tétel szerint Vizinga, kromatikus indexe egy grafikon, nem több, mint Δ + 1.
• k degenerációja gráf egy grafikont, amelyben minden részgráf a csúcsot a mértéke nem nagy k.