Végtelenül kicsi és végtelenül nagy mennyiségben
Definíció. A funkció az úgynevezett végtelenül kicsi a lényeg. if.
Ez a funkció a végtelenül nagy a ponton. if.
Ez a fogalom nem vonatkozik az „általános” funkció nélkül pontot. Nincs egyszerű „végtelenül kicsi funkciók” csak a „végtelenül kicsi funkciót ezen a ponton.” Ez a tulajdonság viselkedése a függvény egy adott helyen. Így, egy végtelenül-kicsi.
Nyilvánvaló, hogy ha egy kis inf pontot, akkor végtelenül nagy ugyanazon a ponton.
Példa. Fknktsiya végtelenül melléklet 1. és végtelenül nagy a 2. pontban.
Végtelenül azt mondta, hogy hasonló. ha van legalább egy, a határértékek vagy.
Ha. sőt. A két függvények végtelenül kicsi egy nagyságrenddel. By the way, akkor. hogy van, a két szélső értéket véges számú helyette. Ha ez lenne a második lenne a limit.
Ha ugyanabban az időben. azaz. A két végtelenül nevezett EKVIVALENTNYMIEto speciális esete a helyzetet, amikor ugyanabban a sorrendben.
Ha a hívott végtelenül kicsi magasabb rendű, mint ezt.
Példa. . A funkciók és ugyanabban a sorrendben a 0 pont.
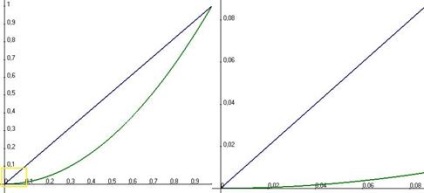
Példa. . valamint,
ez egy magasabb rendű, mint ezt. És bár mindketten hajlamosak 0, de a sebesség ez a folyamat teljesen más. Ha megnézzük a menetrendek nagy nagyítással a származás, a parabola szinte megkülönböztethetetlen a 0x tengely.
Harmadik fokozat - magasabb rendű még, akkor kevesebb, mint egy parabola. Ahogy meglátjuk, bár hajlamosak 0, de a nullák, mint teljesen más erő.