Két algoritmusok meghatározására sor Pareto-optimális megoldások multikritériumos lineáris
A tervezés, fejlesztés és értékelése a minőség minden komplex rendszerek, amelyek magukban foglalják szoftverek és rendszerek, szükség van egy olyan rendszer meglehetősen ellentmondásos követelményeket. Ha ezek a rendszer követelményeinek lehet kifejezni formájában mennyiségi mutatók egyéni (magán kritériumok - h-kritériumok), a tervezési probléma lehet hivatalossá a vektor formájában probléma multiobjective matematikai programozás (VZMP):
ahol (1) azt jelenti, hogy semmiféle növekedést a r-h kritériumok javítja a rendszer [1] X = (xj) N - (DMP oldat) paraméterek által irányított döntéshozó (DM); Dx - megvalósítható régió döntéshozói.
Továbbá feltételezzük, hogy a H-kritériumok lineáris, és a terület zárva van, és arra korlátozódik, hogy a lineáris egyenlőtlenségek. Ezután többszempontú (vektor) LP probléma (VZLP) felírható:
ahol a felvétel jobb határa képviselt, mint egy nem-negatív lineáris függvények (változók) [2].
VZLP (3), (4) nem egy optimalizálási probléma, hogy hogyan tudsz mondani optimalitásával megoldás csak abban az értelemben, az egyik h-teszt a népesség (3). Tekintettel az összessége (3) beszélhetünk csak egy racionális, hogy kisebb vagy nagyobb mértékben gyakorlatilag elfogadható, kompromisszumos megoldást, ahol esetleg egyik sem r-h kritériumok nem veszi fel a maximális értéket. Különféle eljárások léteznek, hogy megtalálják a racionális megoldásokat [1-8], azonban előfeltétele minden ennek a megoldásnak az, hogy nem lehet javítani legalább egy órás kritérium, hogy míg sem a fennmaradó nem romlott az értékét. Ez a „unimproveable” megoldás az úgynevezett Pareto optimális [1-3], vagy rövidítve P-optimális.
Így a megoldás bármely multiobjective feladatok vagy elkezdi keresni a teljes készlet n-optimális megoldások (n-set), ami kell, és a végső, kompromisszumos vagy befejezi ellenőrzi előre megoldások n-optimum, és ha szükséges, az ezt követő javulás néhány órán kritérium romlása nélkül értékek maradt.
A fő célja ennek a papír, hogy alakítsanak egy meglehetősen egyszerű és könnyen formálissá egy algoritmust:
- a teljes készlet Pareto-optimális megoldások VZLP (DPX);
-, hogy a döntés az X ¢ P-optimális, és ha szükséges, hogy megtalálják a legközelebbi neki P-határozatot.
A javasolt módszer a szükséges formai feltétele P-optimális megoldások X ¢ [1; 2]: oldat X ¢ÎDx P-optimális, ha nem létezik más megoldás XÎDx, miáltal hogy megfelel a feltételeknek:
„K: Lk (X) ³Lk (X ¢), t.e.Dk = Lk (X) -Lk (X ¢) ³0, (5)
míg legalább egyikük - szigorúan (DK1> 0).
Megfogalmazni feltételeit az algoritmus (5) célszerűen képviseli formájában a LP probléma (ZLP)
alatti megszorítások Dk = Dk (X) ³0, „k = 1; R (7).
Állapot (7) egy geometriai értelemben - egy tartomány által alkotott metszéspontja R n-dimenziós fél-terek által meghatározott egyenlőtlenségek (7). Ez a kompatibilitás rendszer (7) képez, egy kis teret - a kúp csúcsa X ¢. Minden pont a kúp összehasonlítva fokozott X ¢, oldatot (a továbbiakban: a kúp dominancia kúp, kúp-d).
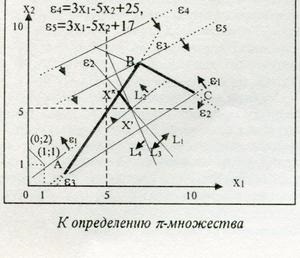
A meghatározás szerint a p-készletek
Ábra részletét kúp, egy olyan területen, Dx, egy szegmens X ¢, Xp a következő VZLP:
L2 (X) = - X1 + X2 + 10, ® max e2 = -x1-4x2 + 34, Dx
L3 (X) = - X1-X2 + 16, X E3 = 2x1-x2-5,
L4 (X) = - 2x1-x2 + 30 (8) „i, j: xj, ei³0 (9).
Degeneráltsága a d-kúp miatt a teljes ellentéte h-kritériumok L1 és L3 - a gradiens vektor különböznek csak a jelek. Fizikailag ilyen esetben nem kerülhet sor, mert Ha például, L1 maximalizálni kell a rendszer megbízhatóságát, az L3 - minimalizálja az a megbízhatósága. Azonban a hivatalos felülvizsgálatát ilyen rendszer h-kritériumok nem veszít jelentését.
Eltolása a pontot az X ¢ be az e-kúp, egy javított megoldást. Ez a javulás (ebben az esetben, a kritériumot h-L2) esetleg akár egy elmozdulást Xp pontot, amikor a teljes kúp-d, kivéve a felső, kívül lesz a domain Dx. Mivel a választás a pont X ¢ nem befolyásolja a formája és irányultsága d-kúp (amely megfelel a párhuzamos elmozdulását a n-dimenziós oktáns), lehetőség van arra, kiválasztásával X ¢ különböző Dx pontot megjegyezni, hogy minden P-mnozhstvo összeget pontok szélek (élek) AB és BC mintát.
Így, az oldatok ZLP (6), (7) bármely választott felső D-kúp X ¢ a pozitív oktáns [3] az alábbi következtetéseket: ha Dmax> 0, akkor a D-kúp létezik, és a P-beállított összeget bizonyos arcok a több dx; ha Dmax = 0, akkor (7) kompatibilis csak az X ¢, ami azt jelenti, hogy bármely pontján az X ¢ÎDx n-optimális (DPX = Dx).
Abban az esetben, Dmax> 0, X pontban ¢ kell egymást követően kiválasztott minden területén metszettel Dx. Ez egyenértékű azzal, mintha a rendszerhez (7) egy másik egyenlőtlenség megfelelő i-edik felület (ei³0). Ha során megoldások ZLP kritérium D (6) növekedni fog, ez nem kötődik a P-optimális, és ha Dmax = 0 - kötött belép több DPX. M ellenőrzése minden arcok a szimplex Dx, megtaláljuk a P-set DPX.
A transzfer szett (6) szélén Dx társított további számítások azonban vertex X ¢ d-kúp ajánlatos, hogy válasszon egy fix pont X ¢ = (1) [4], és ugyanaz az arc, a szimplex átadási pont Dx. Ezután, csökkentve az elemi transzformációk, csökken az a pont X ¢ = (1) n ZLP (6) és (7) felírható:
A transzformált arc a szimplex vannak írva, ugyanakkor:
Szemléltesse Process Solutions példa (8) (9). Szerint (10) - (11) lehet írva ZLP rendszer (12) a algebrai és táblázatos T1:
T1 x1 x2 T2 x1 D1 1 1 1 T3 e2 D1
D = -3x1 + 3®max, D -3 3 0 0 D -3 3 D -1 -4 0
D1 = x1 + x2-2, D1 1 1 -2 x2 -1 január 2 x2 1
D2 = -X1 + x2, D2 -1 0 1 D2 -2 február 1 D2 0
D3 = -X1-X2 + 2, D3 -1 -1 2 -1 0 0 D3 D3 0 (13)
D4 = -2x1-x2 + 3, D4 -2 -1 3 1 D4 -1 -1 0 D4
E1 = -5x1 + 7x2-2, e1 -5 -2 e1 -12 7 július 12 e1 0
e2 = -x1-4x2 + 5, E2 -1 -4 5 e2 3 1 -4 -3 x1
E3 = 2x1-x2-1. e3 2 -1 -1 E3 3 0 -1 -3 e3
A szimplex módszer [6, 7] megoldott ZLP, otcherknutaya T1 kettős vonal. ei korlátozások által rögzített kettős vonal egyszerűen fordította képletek közönséges Jordan kivételek (OZHI). Lépés után OZHI (helyettesítő D1 «X2, T1) kapott optimális megoldás. Mivel Dmax¹0 (Dmax> 0), a kúp-d létezik, és így, p-set arcok képeznek néhány régióban Ax. Ezeket az arcokat határozza meg, kivéve azokat, amelyek arcokat nem tud belépni a Ax. Számukra ha D> 0, van ei³0 (e1 arc). Nem i fennmaradó széleit sokaságát képezik I- =. Lépcsőzetes vizsgálati arcok iÎI- felfedi arcát epi. Így például, hozzátéve, hogy a rendszer (11) szembe e2<0, после шага ОЖИ (e2«х1,Т2) получим решение X0=(1;1) и Dmax=0, из чего следует p-оптимальность грани e2 области Dх. То же для e3 (см.рис.).
DPH elleni hamis megoldásokat a rendszer (4) ki kell zárni arcok nem képezik határait a domain Dx. Erre a sorozat „ei³0 helyébe határvonal EI = 0. Ha a rendszer (4) válik inkompatibilis, majd ei³0 egyenlőtlenség eliminálódik. Kizárt és lineárisan függő egyenlőtlenség (lásd. Ábra. E4, E5) [5]. Feltételezve, hogy ez a szűrés képződik , tudjuk írni az eljárás a probléma megoldására.
1. algoritmus határozza meghatározó p-
20. Problémák ZLP (10), (11), ezzel egyidejűleg számítva (12)
30. Ha Dmax = 0, írásban Dph = Ax, menjen 110
40. Távolítsuk a (12) korlátozzák ei³0, levelet (határozza meg) több I - =
50. Ha I- = 0, megy (100)
60. Kapcsoljuk be a szélén EI, iÎI-, hogy a rendszer (11), és oldja ZLP (10), (II) + EI
70. Ha Dmax¹0, i kizárt I-, megyek 40
80. beszúrása EI kötött Dph (EI = epi), i kivéve I-
90. Ha I-¹0, menjen 60
Ha Dph talált, az a kérdés, tulajdonjoga néhány tetszőleges pont X ¢ csökkenti a helyettesítés annak összetevői X j ¢ (9), valamint a számítás a reziduumok EI. Ha legalább az egyik közülük megfelel a P-állítva a nem-negativitás a reziduumok nulla, X ¢ÎDPH.
Ahhoz azonban, hogy ellenőrizze az U-optimum X ¢ nem kell építeni az összes U-set. Elég megoldani ZLP (6), (7) és (4). Ha Dmax = 0 - X pontban ¢ P-optimális. Amikor Dmax¹0 jobb megoldás lesz megtalálható (lásd. Ábra. X ¢ és Hp).
A [8], a több n-VZLP meg lehet találni a set ZLP megoldások korlátok (4), és egy célfüggvény kapunk lineáris kombinációja H-kritériumok: [6]
az összes lehetséges értékét súlyozási együtthatók h kritériumok - ak.
A hátránya ennek a megközelítésnek abban a tényben rejlik, hogy ezek csak akkor mutatható ki a P-megoldó, feküdt a a régió határain Ax. A [2] az esetben Dph = Dx választhatnak egy ilyen vektor együtthatók AO = (ak), amelyek minden együttható CJ a "konvolúció" (14) eltűnik. Ez a megközelítés vezethet be hamis n-megoldásokat. Például, figyelembe ao = (0,5; 0, 0,5, 0) a (8), akkor megállapíthatjuk, hogy Dph = Dx, de látható az ábrán, hogy ez nem így van.
Mi jelzi a számítási eljárás, amely megvalósítja azt az elvet a „konvolúciós”, és hogy megoldja ezt a hiányosságot. A módszer abban áll, hogy a kimutatására P-Making található i-edik felülete (4), szükség van, kiválasztásával a vektor ai eleget két feltételnek: az együtthatók CJ (14), és aij i-edik szembe kell, hogy arányos legyen minden alkalommal j; Ezeket a tényezőket különböző jelek, hogy biztosítja a szélsőséges érték „konvolúció” az i-edik (i = 1; m) arcát. Feltételezve, hogy az arányosság együttható hi pozitív, ezeket a feltételeket figyelembe véve (14) felírható:
Az i-edik arcát az egyenletrendszert (16) továbbá kész, az oldat, amely lehetővé teszi számunkra, hogy fennáll-e a hi> 0 vektor ai = (aik), amely végrehajtja a szükséges feltételeket ez az arc.
Korábban jelölt helytelen formálisan társított az esetben, ha hi = 0 a (16). A probléma megoldásához elég esetben Dph = Ax társítani a helyzetet, amikor az összes m arcok simpeksa Dx szerepelni fog a P-set. Ez fog kialakulni ellenőrzése után m élek. Így, meghatározása a P-beállított ez a megközelítés csökkenti az m-szeres oldat (16), vagy, pontosabban, az oldathoz ZLP: [7]
ahol Oj - változókat, amelyeket át kell alakítani, hogy a nulla (null változók); hi - arányossági tényező.
Meg kell jegyezni, hogy mind az első és a második esetben, hogy egy megoldás, hogy a végén ZLP általában nincs értelme. Csak el kell arról, hogy a D> 0 (az első algoritmus) vagy hi> 0 (második algoritmus), amely biztosítja szemben téves következtetéseket nem ellenőrizte arcát.
Algoritmus 2 meghatározások p-
30. Problémák ZLP (17), (18) (maxh)
40. Ha Hmax £ 0, ei megszüntesse a sorban, menjen 60
50. Írja ei = epiÎDPH
80. Ha | Dph | ¹m menjen 100
90. Írja Dph = Ax
Összhangban kapott algoritmus megoldása a következő:
h1max = 0, (AC); h2 = 0,1, (BC); h3 = 1/7 (AB). (19)
Amint a (19), az AU arc nem szerepel a beállított P (h1max> 0).
Ugyanakkor számítási egyszerűség mindkét algoritmus, csak az első megközelítés a következő három jellemző:
- lehetséges, hogy ellenőrizze az U-optimalitásával bármely döntés X ¢ÎDx, és VZLP és megtalálni a legközelebbi U-optimális anélkül, hogy keressen a teljes P-készletek;
- esetében Dph = dx elején található a számítások, akkor nincs szükség utólagos számítások eltűnik;
- anélkül, hogy a hozzáadott komplexitás lehetséges, hogy ellenőrizze a U-optimalitásával néhány tetszőleges pont X ¢ÎDx egy általános probléma MP (1), (2).
Az utóbbi esetben elegendő, például a kezdeti adatok tömb SKJ || || használjon egy mátrixot származtatott értékek x pontban ¢ÎDx (közelítés):
A válasz formájában kapjuk az „igen”, „nem”, nem tartalmaz semmilyen utalást (abban az esetben „nem”) a kutatás további iránya az a P-optimális megoldások. Abban az esetben, „igen”, akkor csak beszélünk a helyi P-optimális megoldást a problémákra rejlő keresést globális szélsőérték vagy U-set. Azonban továbbra is egy lehetőség, hogy olyan megoldásokat találjanak, U-rendezett felsorolás pont XÎDx, mint a numerikus rács csomópontok vagy véletlenszerű keresési módszert.
Összefoglalva, azt látjuk, hogy ha az eredeti VZLP van m1-egyenlőség korlátok, akkor írja le azokat a kanonikus formában legfeljebb m1 OZHI lépéseket (lehet lineárisan függő) VZLP csökkentette a forma (3), (4), de m1 csökkentett száma szabad változók.
1. Jurij Dubov hadnagy SI Yakimets VN Többkritériumos modellek kialakulása és választás rendszerek. - M. Nauka, 1986. - 295 p.
2. VV Podinovskii VD Nogin Pareto-optimális megoldás multiobjective problémákat. - M. Nauka, 1982. - 256 p.
3. Larichev OI Polyakov OA Ember-gép-készítés eljárások mnogokriterialnyh MP megoldásokat a problémákra (Review). Közgazdasági és matematikai módszerek. - 1980 - T.16, nem. 1. - P. 127-145.
4. Germeier YB Bevezetés a Operations Research. - M. Nauka, 1972. - 383 p.
6. DB Yudin Holstein EG Célkitűzések és módszerek a lineáris programozás. - M. baglyok. rádió, 1969. - 736 p.
7. Bersin EA Optimális forráselosztás és a játékelmélet. - M. Rádió és kommunikáció, 1983 - 183 p.
8. S. Karlin Matematikai módszerek és az elmélet játékok, programozás és a közgazdaságtan. - Mir, 1964 - 838 p.