A tömeg és a lendület a foton
A törvény szerint az arányosság tömeg és az energia energia ε pho-tone egyenlő
ahol C - a fénysebesség vákuumban.
A hipotézis szerint a fotonenergia egyenlő Planck
Ezekből az egyenletekből kapjuk a kifejezést a tömege a foton
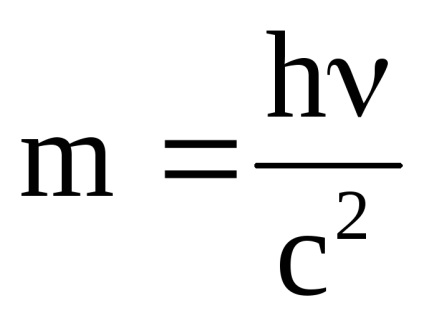
figyelembe véve azt a tényt, hogy a
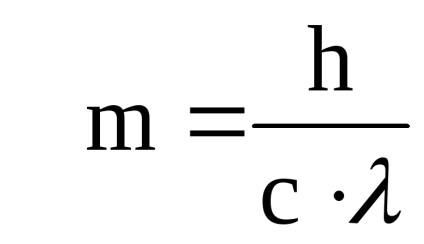
A kifejezés az impulzus p az általános formája:
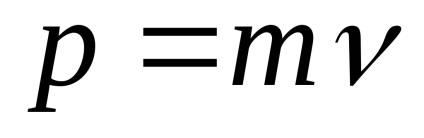
Mass foton többi nulla. Quantum elektromágneses sugárzás már csak terjednek a térben a fény sebessége.
Mivel foton lendület, a fény esik a felszínen a test derül ki, hogy a kád nyomást. Tegyük fel, hogy a felület s = 1 m 2 az átlátszatlan test egy időben At = 1s esik fotonfluxus, amelyek száma megegyezik a Nb. Ha a test-felület egy reflexiós együttható ρ, hogy ρNf-zitsya fotonok visszaverődik, és (1 - ρ) Nb felszívódik a szervezetben. Minden jelentés tükrözi foton lendülete p1 szervezetben. egyenlő változtatni lendület a foton, azaz
p1 =
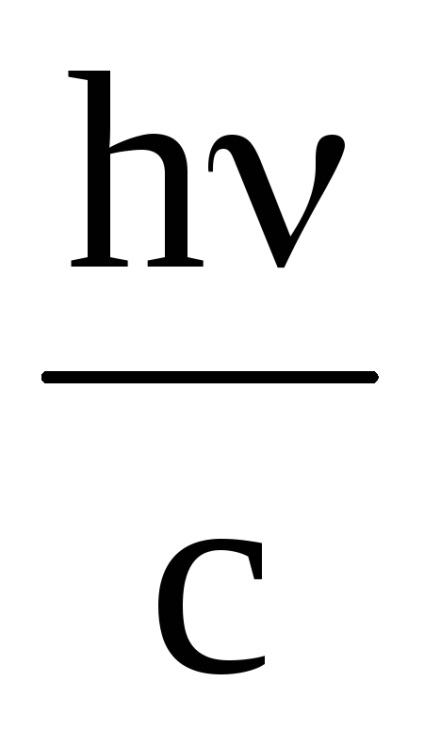
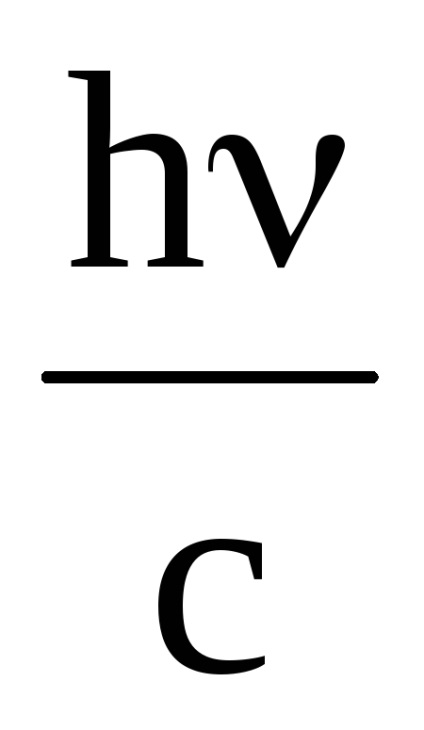
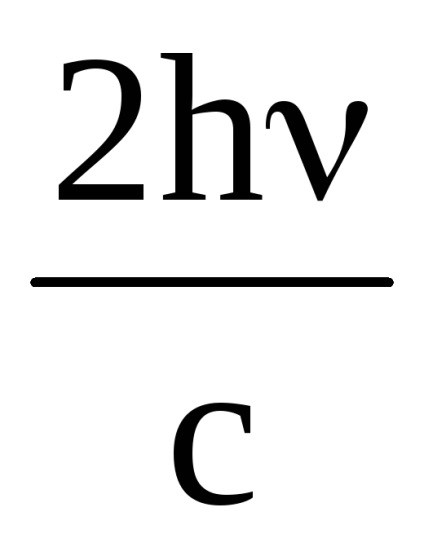
Teljes impulzus kapott 1 m 2 a felület 1 s egyenlő p
p = P1 + P2 ρNf · (1 - ρ) NF =
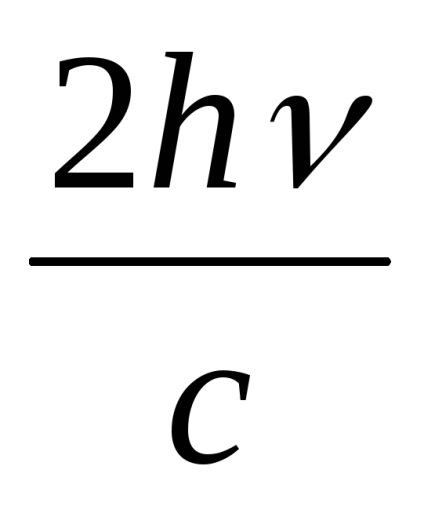
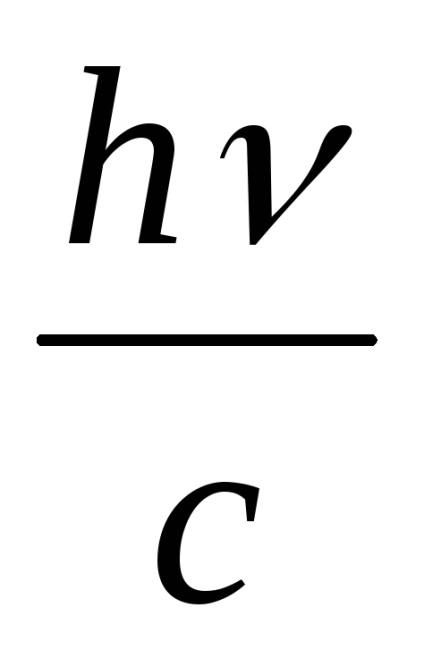
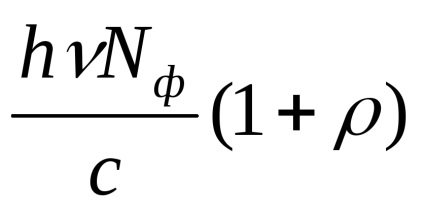
A nyomás egyenlő lesz az impulzus ereje, a felületet kell jelenteni fotonok egység 1. Ebből következik, hogy a teljes lendületet a kapott 1 m 2 1 másodpercig, számszerűen egyenlő a nyomás P.
érték


Ez a kifejezés az a nyomás a fény kapott a kvantum elmélet a fény.
A kifejezés a nyomás a fény felhasználásával kapunk egy ökör-új elmélet a fény. Ha a fém felületén általában beeső elektromágneses hullám, az elektromos tér intenzitása (E) az elektron fog elmozdulni az ellentétes irányba, hogy az irányt a vektor E. Ebben az esetben a mágneses tér a fényhullám a fény hullám indukciós B minden egyes elektron-dy mozgó v sebességgel jár Lorentz-féle erő Fl = EVB, befelé irányuló merőlegesen a fém felületén. Így a fényhullám fog nyomást a fém felületén. A számítások szerint által végzett elektromágneses elmélet Maxwell-RII, könnyű nyomás képlete
ahol Ee - besugárzott felülete, azaz A fluxus fény beeső energia ezen a felületen. Így a nyomás a fény sikeresen magyarázni, mint a hullám-nek, és a kvantumelmélet.
Compton hatás
A szórás az elektromágneses sugárzás szabad vagy lazán kötött elektronok, amelyben egy foton az eredmények-Tate rugalmas ütközés az elektron transzferét nevének része-szíve és az energia, az úgynevezett Compton hatást (az első-TIONS megfigyelt 1923-ban) Compton hatása azt mutatja, hogy a fotonok annak ellenére, hogy a hullám természetét, úgy viselkednek, mint a részecskék és képesek kölcsönhatásba más részecskékkel egy elv emlékeztető rúgás kemény golyó.
Egy beeső foton energiával hv (ábra. 163), ennek eredményeként az ütközések az energia elektron áthalad, és átalakul más fotonenergia hv”, ami mozog szögben Θ a kezdeti mozgásirányával a foton.
A törvény szerint az energiamegmaradás összegének primerenergia hv a foton energiája az elektron nyugalmi és E0 = m0 c 2 egyenlőnek kell lennie az összege az energia a szórt foton hv „és a teljes energia az elektron az ütközés után
hv + m0 c 2 = hv „+ mc 2., ahol
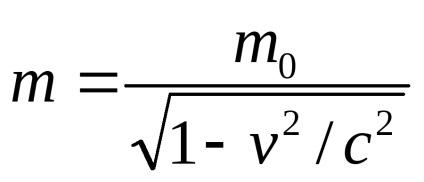
Az ütközés során az elektron és foton végzünk több, és a törvény lendületmegmaradás
p és OM - a kezdeti lendület a foton és az elektron, p „és p” Oe - az impulzusok szétszórva.
Azt feltételezzük, hogy a kezdeti elektron sebessége nulla. ER = 0. Ekkor a foton lendület p =
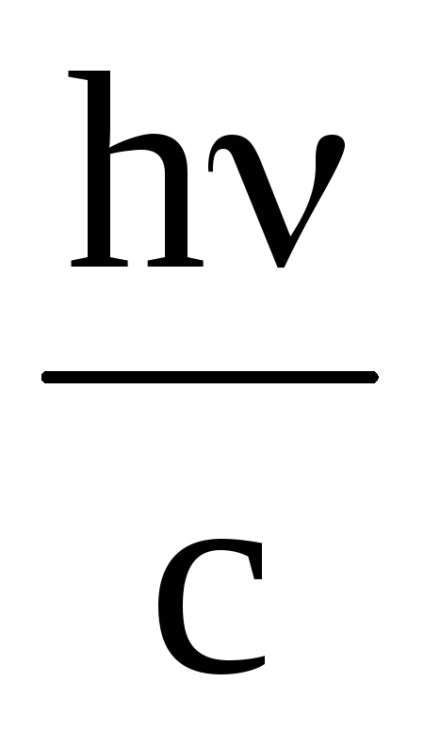
ahol h - Planck állandó; v és ν „- az alkalmazás gyakorisága az eset és szétszórt
és
A vektor diagramok impulzusok (. Ábra 164) a következőképpen:
Egyenletek megoldására az 1. és 2. tekintettel arra a tényre, hogy
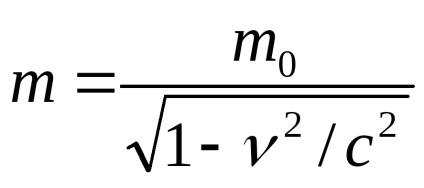
.
Tekintettel arra, hogy csökkentse és megszerezni
.
érték
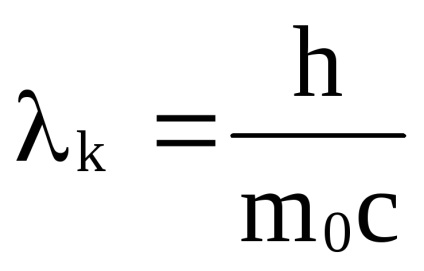
A mozgási energia a visszarúgás elektron (kölcsönhatás után egy foton) egyenlő
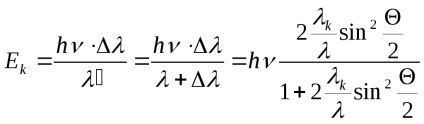
Elektron-bombázásos energia éri el maximális Θ = π, azaz amikor a foton szétszórt az ellenkező irányba
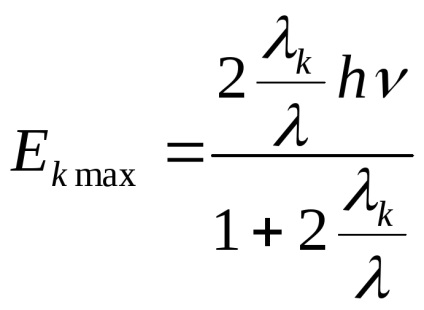
Felszívódás egy foton egy szabad elektron lehetetlen, mivel Egy ilyen eljárás ellentétes a jogszabályok energiamegmaradás és a lendület.
Ez a két arányok kompatibilis csak ν = 0.