A Vieta tétele

Vieta tétele. Példák a megoldásokra

Ebben az előadásban megismerkedünk a kvadratikus egyenlet gyökerei és koefficiensei közötti kíváncsi viszonyokkal. Ezeket a kapcsolatokat először a francia matematikus, Francois Viet (1540-1603) fedezte fel.

Például a 3x2 - 8x - 6 = 0 egyenlethez, a gyökereinek feltárása nélkül azonnal használhatjuk a Vieta tételét, hogy azt mondjuk, hogy a gyökerek összege megegyezik. és a gyökér terméke
azaz - 2. És az x 2 - 6x + 8 = 0 egyenletre a következtetésre jutunk: a gyökerek összege 6, a gyökerek termése 8; egyébként itt nem nehéz kitalálni, hogy mi a gyökerek: 4 és 2.
Bizonyítás a Vieta tételéről. A x 2 és a bx + c = 0 négyzetes egyenlet x1 és x2 gyökeit képletek találják

ahol D = b 2 - 4 ac az egyenlet diszkriminansa. Miután ezeket a gyökereket összekapcsoltuk,
kapunk

Most kiszámítjuk az x1 és x2 gyökerek termékeit

A második összefüggés bizonyított:
Megjegyzés. Wyeth tétel érvényes abban az esetben, ha a másodfokú egyenlet van egy gyökér (t. E. Ha a D = 0), egyszerű ebben az esetben, úgy véli, hogy az egyenletnek két azonos gyökér, amelyre alkalmazzuk a fent említett arányban.
Egy különösen egyszerű forma az x 2 + px + q = 0 csökkentett kvadratikus egyenletre vonatkozó bizonyított kapcsolat. Ebben az esetben a következőket kapjuk:

x1 = x2 = -p, x1 x2 = q
azaz a csökkentett kvadratikus egyenlet gyökereinek összege megegyezik az ellenkezőjellel vett második koefficienssel, és a gyökerek terméke egyenlő a szabad idővel.
A Vieta tétel segítségével más összefüggéseket lehet elérni a gyökerek és a kvadratikus egyenlet koefficiensei között. Legyen például x1 és x2 az x 2 + px + q = 0 csökkentett kvadratikus egyenlet gyökerei.

A Viet tételének fő célja azonban nem az, hogy bizonyos összefüggéseket fejt ki a gyökerek és a négyzetes egyenlet koefficiensei között. Még ennél is fontosabb, hogy Viet tétele segítségével egy kvadratikus trinomiális elemet bővítünk a szorzókra, amelyek nélkül nem fogunk nélkülözni.

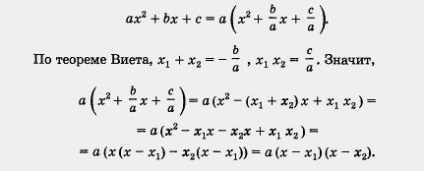
1. példa. A négyzetes trinomiális tényező háromszor 2 - 10x + 3.
A megoldás. A 3x2 - 10x + 3 = 0 egyenlet megoldásával megtaláljuk a kvadratikus trinomiális gyökeret 3x2 - 10x + 3: x1 = 3, x2 =.
A 2. tétel használatával megkapjuk

Van értelme ahelyett, hogy 3x - 1-et írnánk. Végül 3x2 - 10x + 3 = (x - 3) (3x - 1).
Felhívjuk a figyelmet arra, hogy egy adott kvadratikus trinomiális tényezõ faktorizálható és a 2. tétel alkalmazása nélkül a csoportosítási módszerrel:

3x2 - 10x + 3 = 3x2 - 9x - x + 3 =
= 3x (x - 3) - (x - 3) = (x - 3) (3x - 1).

De amint láthatja, ezzel a módszerrel a siker attól függ, hogy vajon sikeres-e vagy sem sikerült csoportosulást találnunk, míg az első esetben a siker garantált.
Példa 1. Csökkentse a frakciót

A megoldás. A 2x2 + 5x + 2 = 0 egyenletből x1 = -2,

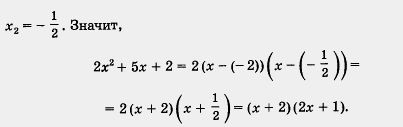
Az x2 - 4x - 12 = 0 egyenletből x1 = 6, x2 = -2 találunk. ezért
x 2 - 4x - 12 = (x - 6) (x + 2)) = (x - 6) (x + 2).
És most csökkentjük az adott törtet:

3. példa Kibővítse a kifejezéseket:
a) x4 + 5x2 + 6; b) 2x + -3
R e w n e. A) bevezetésére az új változó az y = x 2 Ez lehetővé teszi, hogy átírja előre meghatározott expresszió másodfokú polinom a y változó, mégpedig formában y 2 + bu + 6.
Az egyenlet megoldása 2 + + + 6 = 0 esetén a négyzetes trinomiális y 2 + 5y + 6 gyökereit találjuk: y1 = -2, y2 = -3. Most a Tétel 2-et használjuk; kapunk

y 2 + 5y + 6 = (y + 2) (y + 3).
Még emlékeznünk kell arra, hogy y = x 2, vagyis visszatérünk az adott kifejezéshez. És így,
x 4 + 5 x 2 + 6 = (x 2 + 2) (x 2 + 3).
b) Bevezetünk egy új y = változót. Ez lehetővé teszi számunkra, hogy az adott kifejezést kvadratikus trinomiális formában írjuk felül az y változó, nevezetesen a 2y 2 + y-3 formában. Az egyenlet megoldása
2y 2 + y - 3 = 0, megtaláljuk a kvadratikus trinomiális 2y 2 + y - 3:
y1 = 1, y2 =. Továbbá, a 2. tétellel:

Még emlékezni kell arra, hogy y =. vagyis visszatér az adott kifejezéshez. És így,

E szakasz megfogalmazásakor néhány érvet, amely ismét a Viet-tételhez kapcsolódik, pontosabban az ezzel kapcsolatos állításhoz:
ha az x1 számok. x2 olyan, hogy x1 + x2 = -p, x1 x2 = q, akkor ezek a számok az egyenlet gyökerei
Ennek a kijelentésnek köszönhetően sok négyzet egyenlet verbálisan megoldható, nehézkes gyökéralakok alkalmazása nélkül, és négyzet egyenleteket képez az adott gyökerekkel. Adjunk néhány példát.

2) X 2 + 11x + 30 = 0. Itt, X1 + X2 = -11, x2 = x1 30. Megjósolható, -5 x1 = x2 = -6.
Megjegyzés: ha az egyenlet szabad terminusa pozitív szám, akkor mindkét gyökér pozitív vagy negatív; ezt fontos figyelembe venni a gyökerek kiválasztásakor.

3) x 2 + x - 12 = 0. Itt x1 + x2 = -1, x1 x2 = -12. Könnyű kitalálni, hogy x1 = 3, x2 = -4.
Megjegyzés: ha az egyenlet szabad terminusa negatív szám, akkor a gyökerek különbözőek a jelben; ezt fontos figyelembe venni a gyökerek kiválasztásakor.

4) 5x 2 + 17x - 22 = 0. Könnyű látni, hogy x = 1 megfelel az egyenletnek, azaz. x1 = 1 az egyenlet gyökere. Mivel x1 x2 = -. és x1 = 1, akkor megkapjuk, hogy x2 = -.

5) x 2 - 293x + 2830 = 0. Itt x1 + x2 = 293, x1, x2 = 2830. Ha odafigyelünk arra, hogy a 2830-283 • 10 és 293 = 283 + 10, világossá válik, hogy x1 = 283 x 2 = 10 (és most képzeljük el, mi lenne, hogy végre egy számítást, hogy megoldja ezt a másodfokú egyenlet szokásos formulák).

6) Konstruáljon egy négyzetes egyenletet úgy, hogy a gyökerei x1 = 8, x2 = - 4 számok legyenek. Általában ilyen esetben a x 2 + px + q = 0 kismértékű egyenlet alakul ki.
Van x1 + x2 = -p, tehát 8 = 4 = -p, vagyis p = -4. Továbbá, x1 x2 = q, azaz. 8 «(- 4) = q, ahonnan megkapjuk a q = -32 értéket. Tehát, p = -4, q = -32, akkor a szükséges kvadratikus egyenletnek x 2 -4x-32 = 0 alakja van.