Vector elemzés 3
az úgynevezett folyamatos szakaszonként sima, ha a függvény folytonos egy szegmens és osztható véges számú részleges szegmensek pontok
úgy, hogy minden egyes ilyen funkciókat folyamatos származékok, egyidejűleg nem nulla.
Ábra. 64. ábra egy folytonos szakaszonként sima görbe. Pontokon, és ez a folyamatos, de néhány vagy az összes származékok folyamatos (az első ilyen!).
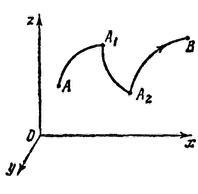
(1) görbe fogjuk jelölni egyetlen betűvel, az ilyen levél. Általában arra utal, nem csak a pontok helye által meghatározott (1) egyenlet, de a sorrendben ezeket a pontokat, amikor folytonosan növekszik előtt. Ebben az értelemben, van egy orientált görbe. Rangsor jelöli a nyíl (64. ábra) -, amikor folyamatosan növekszik pont előtt mozog a nyíl irányába.
Ha van egy függvény, amelynek pozitív származékot folyamatos át néhány intervallumot, és ezáltal, az egyenlet
Ez határozza meg az azonos orientált görbét. Által kijelölt Ugyanebben a levélben csak mondani esetén (1) egyenlet, amely meghatározza azokat a paramétereket, és abban az esetben (1 „) - egy paramétert. Mindkét esetben a növekedés vagy növekedés ettől a megfelelő pontot mozog ugyanabban az irányban.
A másik dolog, ha egy csere, ami a folyamatos negatív származékot a szegmensben. Ebben az esetben, és a folyamatos növekedése felállításának és a nyíl csökkenni fog a geometriai objektumokat kell küldeni a másik oldalon.
Ezért, a görbe (1 „) abban az esetben, fogjuk jelölni egy másik szimbólumot, és azt mondják, hogy van azonos görbe, és aki, de orientációja ellenkező irányba. Néha az eredeti orientált görbe fogja jelölni.
Orientált görbe (1) zárva van, vagy zárt hurok, ha, vagy ezzel ekvivalens, ha
Más szavakkal; ha a paraméter értéke folyamatosan nő, mielőtt a megfelelő pontot a térben terjed zavartalan utat kezdődő és végződő ugyanazon a ponton. Ha a görbe más pontjain nem metszi önmagát, ez az úgynevezett önmagát metsző zárt görbe. Ábra. 65, és megmutatja a önmagát metsző zárt görbe, és ábra. 65, - egy önmagát metsző zárt görbe.

Megjegyzés. A vektor (1) egyenlet a görbe egyenértékű három egyenlet
1. példa Tegyük fel, hogy a görbe egyenlet által definiált
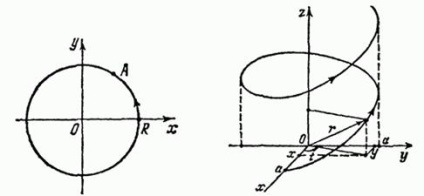
Mivel, ez a görbe a körön origó középpontú. A növekvő 0 pont mozog egy kört az óramutató járásával ellentétes. Ugyanakkor eleget különböző pontokat. És amikor már. Ennélfogva, a zárt kör önmagát metsző görbe (ábra. 66).
2. példa Curve
ahol - pozitív számok, az úgynevezett spirál. Meg lehet a következőképpen állítjuk elő. A szegmens hossza, tengelyre merőleges, egyik vége csúszik tengelyirányban és forog egyidejűleg egy olyan tengely körül, míg a másik végét a szegmens leír egy spirális vonal. Hisszük, hogy az emelő magassága arányos a hosszával a forgásszög tengely. A növekvő pont mozog, ábrán látható. 67. Nyilvánvaló, hogy a hélix található egy oldalsó felületén egy kör alakú henger sugara van, és egy alkotója, a tengellyel párhuzamos.