§ január 1
ε = φ = ω (Rad / s 2), vagy (c-2)
Ha az első és a második derivált a szög φ időben ugyanaz az előjele, a forgás felgyorsul, ha más előjellel - lassú. Ha a szögsebesség állandó, folyamatos forgás (ebben az esetben a szöggyorsulás ε = 0).
2.2.2. Sebesség és gyorsulás a forgó pontokat a test
A sebessége a kerületi pontokat a test nevezik a fordulatszám és a készülék függ a távolság a lényeg, hogy a forgástengely.
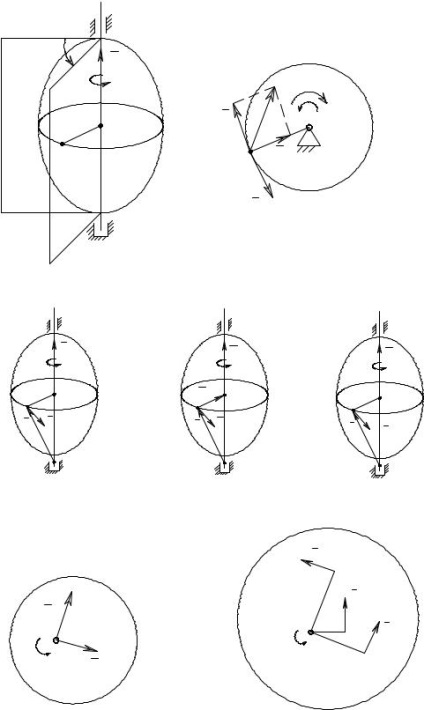
A sebességvektor merőleges a kör sugara által leírt a pont a forgásirányban (2. ábra).
Gyorsulás a pont egy forgó test két összetevője van - a centripetális és a forgási gyorsulás.
A nc = ω 2 és OM OM Bp = ε
Egy vektor irányított attól a ponttól, NC, hogy a forgási tengely körül, egy Bp vektor merőleges a sugár irányába ε.
Komplett gyorsulásvektor geometriai összege a CA és a sp
egy teljes gyorsulás modul határozza meg a képlet
2.2.3. Expressziós vektor sebesség, centripetális gyorsulás és a forgási forgástest pont
Úgy tartják, hogy a szögsebesség és a szöggyorsulás - vektorok mentén irányul a forgástengely, a vektor ω irányul tengely mentén úgy, hogy vége forgása tűnt előforduló óramutató járásával ellentétes irányba, a szöggyorsulás vektor ε is irányul tengelye mentén azonos az irányba, mint ω egy gyorsított forgás, vagy az ellenkező - során lassú.
A forgási sebessége a pontot, és a forgási centripetális gyorsulás képviselheti egy vektort termékek (3. ábra).
egy nc = ω X V = ω x ω X R