Hogyan állapítható meg, milyen időközönként monotónia
Interval monotonitás nevezhetjük egy rés, amelyben a funkciójuk vagy csak növeli, vagy csak csökken. Számos konkrét intézkedéseket, amelyek segítenek megtalálni az ilyen tartományokat funkciókat, amelyekre gyakran szükség algebrai problémák ilyen.
oktatás
Az első lépés a probléma megoldásában a meghatározása az intervallumok, amelyben a függvény monoton nő vagy csökken, a számítás lesz a domain a funkciót. Ahhoz, hogy ezt, meg az összes érvet (értékeket az x-tengely), amelyhez megtalálható az a függvény értékét. Jelölje meg a pontokat, ahol a folytonossági fordul elő. Keresse meg a függvény deriváltját. Ha meghatároztuk a kifejezés, amely képviseli a származék, egyenlő ez nullára. Ezt követően meg kell találni a gyökerei a kapott egyenlet. Ne feledkezzünk meg a különböző megengedett értékeket.
Rámutat, ahol a függvény nem létezik, vagy annak származékát nulla, képviseli a határait időközönként monotonitás. Ezek a tartományok, valamint egy ponttal elválasztva őket, meg kell következetesen az asztalra. Keresse meg a jel differenciálhányados a keletkező lyukakat. Ehhez, helyettesíti az expressziós megfelelő származék, bármely érv az intervallum. Ha az eredmény pozitív, a funkció növeli ebben a tartományban, ellenkező esetben - csökken. Az eredmények bekerülnek az asztalra.
A vonal jelzi a függvény deriváltját f „(x), amely megfelel a rögzített értékeinek érvek szimbólum»+«- ha a derivált pozitív,»-«- negatív vagy»0«- nulla. A következő sorban válassza ki a monotónia az eredeti kifejezést. Fel nyíl növekedésnek felel meg, le nyíl - csökkenő. Megjegyzés szélsőérték pont funkció. Ez az a pont, ahol a származék az nulla. A szélsőérték lehet maximum pontot vagy minimális pontot. Ha az előző függvény a föld emelkedett, és az áram csökken, az azt jelenti, a maximális pontot. Abban az esetben, addig a pontig, működése csökken, és megnöveli - a minimum pontot. Jegyezzük fel a függvény értékei a szélsőérték.
Egyhangúságát - a meghatározása a funkciók a viselkedés a szegmens a valós tengely. A funkció lehet monoton növekvő vagy monoton csökkenő. A helyszínen a monotónia függvény folytonos.

oktatás
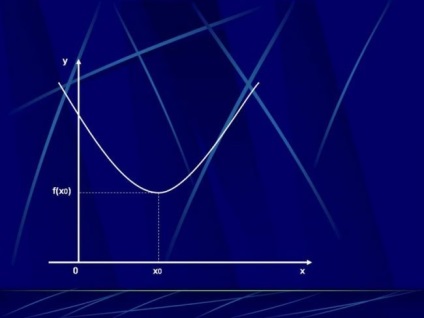
Ha egy bizonyos számszerű intervallum növekedése függvényében az érv növekszik, akkor ezen az oldalon monoton növekvő függvénye. A grafikon a terület monoton növekedés felfelé irányuljon. Ha minden argumentum megfelel egy kisebb érték csökken, mint az előző a függvény értékét, egy ilyen funkció egy monoton csökkenő, és annak ütemezése folyamatosan csökken.
Monoton függvény rendelkeznek bizonyos tulajdonságokkal. Például, az összeg a monoton növekvő (csökkenő) függvény egy növekvő (csökkenő) függvény. Ha megszorozzuk növekvő függvény egy állandó pozitív tényező, ez a funkció elmenti a monoton növekszik. Ha a konstans tényező kisebb, mint nulla, akkor a függvény a monoton növekvő válik monoton csökkenő.
A határait intervallumok monoton viselkedése a függvény a vizsgálat funkciót az első származékot. A fizikai jelentése az első derivált a funkció - a változási sebességének a funkciót. A növekvő sebességének függvényében folyamatosan növekszik, más szóval -, ha az első derivált pozitív egy bizonyos intervallumban ezen a területen monoton növekvő függvénye. És fordítva - ha a valós vonalszakasz első függvény deriváltját nullánál kisebb, akkor a funkció monoton csökken az intervallum határokat. Ha a derivált nulla, a függvény értéke nem változik.
Annak vizsgálatára, a funkció monotonitási egy előre meghatározott intervallumban szerinti első deriváltjának meghatározására, hogy egy adott intervallumban tartozik egy olyan területen a megengedett értékek az érvelés. Ha egy függvény ebben a szegmensben a tengely és differenciálható, megtalálja a származéka. Határozzuk meg a feltételeket, amelyek mellett a származék nagyobb vagy kisebb, mint nulla. Hogy a következtetést a viselkedését a funkciót. Például, a származékot a lineáris függvény egy állandó szám egyenlő a szorzó, ha az érvelés. eredeti funkciója monoton nő, ha a pozitív tényező értéke, negatív - monoton csökken.
Figyelem, csak ma!