Ewald építése - studopediya
Találtunk az állapot, amelyben az X-ray hullám szóródik kristály: a hullám vektor kell lennie a határ egy Brillouin övezetben. Algebrailag, ez a feltétel lehet írott formában (40).
Ha a hullám szóródik, akkor felmerül a kérdés: milyen területeken elszórtan? Azt találtuk, hogy a hullám vektor a szórt hullám eltérhet a hullám vektor beeső hullám csak egy tetszőleges vektor reciprokrács a kristály. Így a hossza a hullám vektorok az eseményről és szétszórt hullámok: k = k0 (. T, hogy a frekvencia a szórt hullámok egyenlőnek kell lennie az esemény gyakoriságát.).
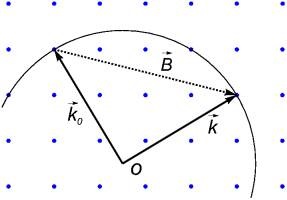
Keresse meg a szórás iránya határozza meg ezeknek a feltételeknek, akkor grafikusan.
Kompatibilis vége a hullám vektor a beeső hullám egy reciprokrács csomópont (ábra. 9). Ábrázolják a reciprok térben k0 gömb sugara a központ O - elején a vektor. A készlet vektorok összekötő az O pont a ponton, amely a gömb felülete - több hullám vektorok. kielégíti a rugalmas szórás, k = k0. De szétszórt hullámok megfelelnek csak azok a vektorok, amelyek a második feltétel szórási kell őket különböztetni egy tetszőleges reciprokrács vektor. Reciprokrács vektor - vektor összekötő két egyes reciprokrács oldalon. Mivel a végén a vektor a reciprokrács egy vonalban van a kerékagy, és a végén a hullám vektor a szórt hullám egybe kell esnie néhány reciprokrács csomópont és ilymódon egy gömb alakú felület. Így a hullám vektorok a szétszórt hullámok - vektor összekötő az O pont a reciprokrács csomópontok, hogy feküdjön a gömbön.
Ha a hullám vektor a beeső hullám szórási nem felel feltételt (40), t. E. nem fekszik a határán egy Brillouin zóna, akkor a gömb nem zavarja a reciprokrács csomópontok, kivéve a végén a vektor. és szórás lép fel.
Kiégett grafikus építési hívják Ewald építése.
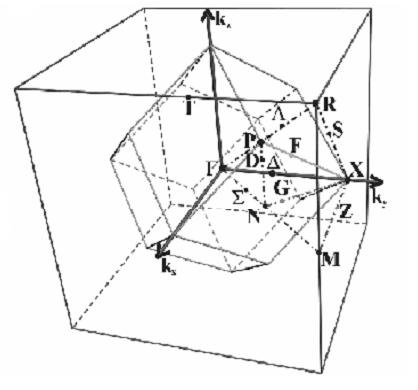
Az első Brillouin zóna egy egyszerű köbös és hexagonális rács
Brillouin zóna - feltérképezése Wigner-Seitz cella a reciprok térben. A közelítése Bloch hullámok időszakos hullámfüggvény szilárd anyag teljesen ismertetett viselkedését az első Brillouin zónában.
Az első Brillouin zóna (gyakran egyszerűen a Brillouin zóna) lehet kialakítani, mint egy térfogata által határolt síkok, amelyek egymástól egyenlő távolságokban tekinthető reciprokrács csomópont szomszédos csomópontok. Egy alternatív definíció tartalmazza Brillouin terület - több pontot reciprok térben, amelyet el lehet érni egy adott csomópont nem haladtak audio Bragg síkon.
Hasonlóképpen, tudjuk, hogy a második, a harmadik és az azt követő Brillouin övezetben. N-I Brillouin zóna - egy sor olyan pontot, amely lehet elérni egy adott csomópont, átlépte a n-1 Bragg síkban.
[Rule] karakterisztikus pontok a Brillouin zóna
Az első zónában az arc-központú köbös rács Brillouin
Bizonyos pontok nagy szimmetria a Brillouin zónában kaptak különleges megnevezések. Központ a Brillouin zóna, vagyis egy pont nulla kvázi lendület, jelöljük a görög betű # 915;. Ha az elektron sávok sávban kristály szerkezete vannak számlálva, akkor hozzáadjuk a hárombetűs kód, amely megfelel a zóna száma: # 915; 1, # 915; 2, stb
A lényeg a szélén a Brillouin zóna által kijelölt latin betűkkel (X, L, és így tovább. D.), és a közvetlen, hogy a vezető a számukra, görög betűkkel (# 916;, # 923; és t. d.). Különleges megnevezések függ a szerkezet a Brillouin zóna egy adott kristályrácsban.
A jobb oldali ábra mutatja az első Brillouin zóna a lapcentrált köbös rács a jellemző pontok megnevezések ott. A piros szín a tétel, amely ismétlése szimmetria véve, lehetséges, hogy kitöltse az egész területet. jellemző pontok
- # 915; - a központ a Brillouin övezetben.
- X - a közepén a kis téren. A vonal, amelynek eredményeként a # 915; X a levél # 916;.
- L - B közepén egy nagy hatszög. A vonal, amelynek eredményeként a # 915; L jelöli # 923;.
- K - a közepén az oldalán a hatszög. A vonal, amelynek eredményeként a # 915; K számára # 931;.
A test-központú köbös rostélyok első Brillouin zóna egy rombododekaéder (lásd alább).
[Rule] Érdekes jellemzői
Annak ellenére, hogy a látszólagos „idézésben matematikai” és levágta a valós életben ezt a koncepciót, a Brillouin terület fontos szerepet játszik a szilárdtest fizika:
- A diffrakciós: a kristályrács diffraktálja csak a sugarak a hullám vektor, amely végződik a határ a Brillouin zóna.
- Megléte miatt a periodicitás a kristályrács, és különösen a Brillouin zóna a kristályok a tiltott és az engedélyezett energia kimondja (lásd. A zenekar elmélet). A megjelenése szalaghézagjaival annak a ténynek köszönhető, hogy egy bizonyos hosszúságú elektronhullámokkal a Brillouin zónahatáron feltétel bekövetkezik Bragg reflexió és az elektron hullám visszaverődik a határ a zónában. Fizikailag ez egyenértékű egy állóhullám, és így, a csoport sebesség az elektron hullám nulla. Így van egy intervallum tiltott frekvenciák (energiák).