Az egyenlet egyenletesen gyorsuló egyenes vonalú mozgás
Találunk kinematikai törvénye egyenletesen gyorsuló egyenes vonalú mozgás. Ahhoz, hogy ezt a képletet (1.6), (1.11) és (1.13). Ezek, az következik, hogy s = VaV · t = (v0 + V) · t / 2 = (2v0 + a) · t / 2,
ezért
Ha a kezdeti test sebessége egyenlő nullával (v0 = 0), akkor
A (1.14) és (1.15) meghatározza pályaszakaszának a test egy egyenletesen gyorsuló egyenes vonalú mozgás (test mozgása modul nem változik a mozgás irányát). Abban az esetben, amikor a test mozog az x tengely .A pont a koordináta x0. a általános képletű (1,14) kapjuk egy egyenletet, amely kifejezi a függőség a koordinátáit a szervezet idővel. mint
Képlet (1,16) van az egyenlet egy egyenes vonalú egyenletesen gyorsuló mozgás (kinematikus törvénye mozgás). Meg kell jegyezni, hogy a (1.16) v0x Hvostov és lehet pozitív vagy negatív, mivel ezt a vetületet vektorok v0 és míg az x tengely.
Az előre irányuló mozgás a test minden pontját a test mozog az azonos, és ahelyett, hogy mozgás minden pont a szervezetben, akkor lehet, hogy fontolja meg a mozgás csak az egyik pontot.
Főbb jellemzői a részecske mozgás: mozgáspályát, elmozdulása az a pont, pályaszakaszának általa, helyzet, sebesség és gyorsulás.
Amely mentén anyagi pont mozog a térben, az úgynevezett pályáját.
referencia-rendszer - egy gyűjtemény a test referencia koordinátarendszer és a referencia ideje a rendszer kapcsolódó test, amelyhez képest a mozgás vizsgálták (vagy egyensúlyi) bármely más anyagból pontok vagy tel.Matematicheski test mozgását (vagy anyagi pont) tekintetében választott referencia rendszert ismertetnek az egyenletek, amelyet beállított változott az idő t koordináták meghatározó helyzetét a test (pont) ebben a referenciakeretben. Ezek az egyenletek hívják az egyenletek a mozgás. Például, derékszögű koordinátái x, y, z mozgása által meghatározott ponton az egyenletek x = f1 (t), y = f2 (t), Z = f3 (t) .A bármely modern fizika a mozgás relatív mozgás a test és figyelembe kell venni csak tekintetében bármely más szerv (szerve referencia), vagy a rendszer a szervek. Nem adhatja meg, például, mint a Hold mozog egyáltalán, csak akkor tudjuk meghatározni a mozgás, például képest a Föld, Nap, csillagok, és így tovább. N.
5.Dvizhenie pont kerülete mentén. Sebesség és gyorsulás görbe vonalú mozgás. Nor-mal és a tangenciális gyorsulás.
Körkörös mozdulatokkal elég gyakori a világ körülöttünk: a forgatás minden szilárd test körül egy rögzített tengely minden pontja a testület mozog körökben. Mivel minden körökben hasonlóak, akkor elegendő, hogy leírja a mozgás az egyik közülük, hogy a forgatást a szilárd test. Továbbá, egyenletes mozgás kerülete mentén a legegyszerűbb görbe vonalú mozgását.
Hagyja, hogy a tömeges pont mozog állandó sebessége v modulusa kerületének sugara R.
mozgás a test egy kört egy speciális esete a görbe vonalú mozgás. Valamint egy mozgásvektor kényelmes vizsgálni a szögeltérésének # 916; # 966; (Vagy forgási szög) radiánban (ábra. 1.6.1). Az ív hossza van társítva kormányzási szög aránya
Abban a kis elfordulási szögek # 916; l ≈ # 916; s.
Ebben a képletben # 916; # 965; # 964; = # 965; 2 - # 965; 1 - módosíthatjuk a modul sebesség alatt az időintervallum # 916; t.
Irányban teljes gyorsulásvektor meghatározzuk minden pontján a kör alakú nyomvonal értékeit normális és a tangenciális gyorsulások.
Sebesség és gyorsulás görbe vonalú mozgás.
Görbe vonalú mozgás bonyolultabb mozgás, mint az egyenes vonalú, mint akkor is, ha mozgás egy síkban, a két koordináta változik az állapot a szervezetben. A sebesség és a gyorsulás a test folyamatosan változik irányba, és általában, és a modult. A pillanatnyi sebessége a test görbe vonalú mozgás irányul bármely pontján a pálya érintője a pálya irányába elvonási tochke.Etot pillanatnyi sebességét is megerősítette megfigyeljük, hogy a permet a mozgó # 8209; a kerekek megcsúszás jármű vagy szikrák a köszörülés részek a forgó köszörűkő .Ha az irányt a görbe vonalú mozgás sebessége a test változik, és ez a mozgás nem egyenletes, akkor is, ha a sebesség a modul állandó marad.
Gyorsulás görbe vonalú mozgás.
Figyelembe véve a görbe vonalú mozgás a test, azt látjuk, hogy a sebesség különböző különböző pontjain. Még abban az esetben, ha a nagysága a sebesség nem változik, de van egy irányváltás a sebesség. Általában a változás és a nagysága és iránya skorosti.Takim, a görbe vonalú mozgás mindig van változás sebessége, t. E. Ez a mozgás felgyorsult. Annak meghatározására, ez a gyorsulás (nagyság és irány) van szükség, hogy megtalálják a változás sebességét, mint vektoron, r. E. Szükséges, hogy megtalálják a változás a nagysága és iránya változás skorosti.Pust, például, egy pont, mozgó görbe vonalú (ábra. 49) volt egy bizonyos ponton a sebesség v1 de miután egy kis ideig - V2 sebesség. Speed változás a különbség a vektorok V1 és V2. Mivel ezek a vírusok különböző irányokba, szükséges, hogy ezeket a vektor különbség. Fordulatszám változtatásra van kifejezhető egy vektorral w, ábrázolt, átlós a paralelogramma oldalon, a másik oldalon v2 v1. Gyorsulás hívjuk az arány a változás mértéke az időtartamot, amely alatt a változás bekövetkezik. Tehát, valamint a gyorsulás
és az az irány egybeesik a vektor w.
Azáltal t elég kicsi, megkapjuk a koncepció pillanatnyi gyorsulás vektor (lásd 16. §); t egy tetszőleges vektor egy képviseli az átlagos gyorsulást az időintervallum t.Napravlenie görbe pályájú mozgás gyorsulás nem esik egybe az irányt a sebesség, míg ezek irányok egybeesnek hogy egyenes vonalú mozgást. Ahhoz, hogy megtalálja az irányt a gyorsulás vektor görbe vonalú mozgás, elegendő összehasonlítani a sebesség irányát két közeli pont a pálya. Mivel a sebesség érintőleges a pálya, a pálya elme maga a következtetés vonható le, milyen irányba a pálya irányított gyorsulás. Sőt, mivel a sebesség különbség a két közeli pont a pálya mindig irányul az irányt, ahol a pályája ívelt, az azt jelenti, és gyorsulás görbe vonalú mozgás mindig irányul a konkáv a pálya. Például, amikor a labda tekercs mentén íves csúszda (ábra. 50), a gyorsítást részek AB és BC mindig irányul, amint azt a nyilak, és ez független attól, hogy a labda gurul A-ról C, vagy a fordított irányban.
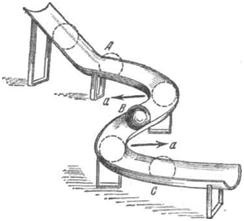
Ábra. 50. Gyorsulás a görbe vonalú mozgás mindig irányul a konkáv straektorii.
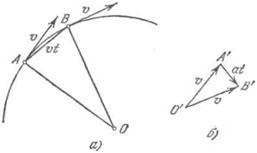
Ábra. 51. származtatása képletek a centripetális gyorsulás.
Tekintsük a egyenletes mozgás egy pont egy görbe pálya mentén. Azt már tudjuk, hogy ez - a gyorsuló mozgás. Keressük a gyorsulás. Ez elég ahhoz, hogy a gyorsulás a különleges esetben, egyenletes körmozgás. Vegyünk két közeli A és B pozíció a mozgó pont megfelelő kis időintervallum t (ábra. 51 a). A tárgy mozgási sebességét pont A és B jelentése azonos nagyságrendű, de különböző irányba.
Találunk a különbség a sebesség, a szabály a háromszög (ábra. 51, b). Háromszögek OAB-hez és O'A'V „hasonlóak egyenlőszárú háromszög egyenlő csúcsszögtartományokon. A hossza az oldalsó A'B „képviselő -os növekmény alatt az időintervallum t, lehet egyenlővé meg, és ahol - az érték a kívánt gyorsulás. Egybevágó mellé AB húrja AB ív; mert a kis hosszúságú ív a húrt feltételezhető, hogy körülbelül ívhossz, azaz a. e. vt. Továbbá, 0'A '= 0'B' = v; OA = OB = R, ahol R - sugara pályáját. A hasonlóság háromszögek, ebből következik, hogy a kapcsolat egybevágó fél ezek közül:
ahol megtaláljuk a szükséges gyorsulást a legnagyobb:
gyorsulás iránya merőleges a húrt AB. Kellően kicsi időközönként kell kiindulni, hogy a érintő ív majdnem azonos a húrt. Ennélfogva gyorsulást lehet tekinteni merőleges ( „normál”), hogy az érintő a röppálya t. E. radiálisan közepe felé a kör. Ezért ez a gyorsulás az úgynevezett normális vagy centripetális gyorsulás.
Ha a pálya - nem kör, hanem egy tetszőleges görbe vonal a képletben (27.1) meg kell tenniük a kör sugara legközelebb a megfelelő görbe ezen a ponton. Az irányt a normál gyorsulás és ebben az esetben ez lesz a normális, hogy az érintő a pályára ezen a ponton. Ha a görbe vonalú mozgás a gyorsulás állandó nagysága és iránya, akkor találtam az arány a növekmény a sebesség vektor hosszát, amely alatt ez a növekedés történik, nem számít, milyen az időkeret. Ezért ebben az esetben, a gyorsítási vektor megtalálható a vektor általános képletű
hasonló képlet (18,1) az egyenes vonalú mozgás állandó gyorsítással. Itt V0 - sebességvektor a test a kezdeti időszakban a t idő, a v - sebességvektor az utolsó pillanatban promezhutka.Normalnoe gyorsulás - egy eleme a gyorsulás vektor, irányított mentén merőleges a pálya egy adott pont a pályája mozgás a test. Azaz, egy normális gyorsulásvektor merőleges a lineáris sebesség (lásd. Ábra. 1.10). Normál gyorsulás jellemzi a gyors változás az irányba, és jelöljük az N betű. normál gyorsulásvektor irányul mentén a görbületi sugár traektorii.Tangentsialnoe (tangens) gyorsulás - egy komponense a gyorsulási vektor mentén irányul érintő a pálya ezen a ponton pályája. Tangenciális gyorsulás jellemzi a gyors változás modulusa a görbe vonalú mozgás.
Ábra. 1.10. Tangenciális gyorsulás.
A tangenciális gyorsulás vektora iránya # 964; (lásd az 1.10. ábrát) egybeesik a lineáris sebesség irányával vagy azzal ellentétes irányban. Vagyis a tangenciális gyorsulásvektor egy tengelyen fekszik, a tangens körrel, ami a test mozgásának pályája.