Hogyan számoljuk ki az összeget a különböző geometriai testek
Egyes képletek más értékei. Az kijelölése lesz szó a megjelenése ilyen igény.
Prism, egy doboz (közvetlen és ferde), és egy kocka
Ezek a szervek egységes, mert nagyon hasonló, és a képlet, hogyan kell kiszámítani az összeg megegyezik:
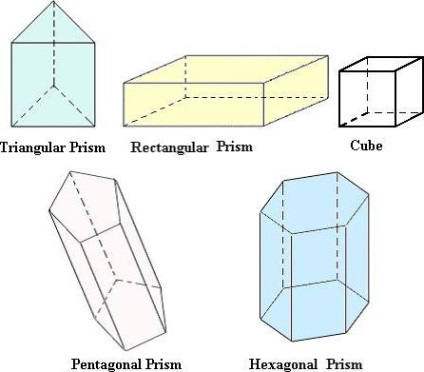
Változik csak S0. Abban az esetben, paralelepipedon számítjuk, mint egy téglalap vagy négyzet alakú. A prizma bázis lehet egy háromszög, paralelogramma, téglalap, vagy más tetszőleges sokszög.
Cube formula nagymértékben egyszerűsödik, mert az összes méretek:
Piramis, tetraéder, csonka gúla
Van egy képlet a fenti, első szervek kiszámításához térfogata:
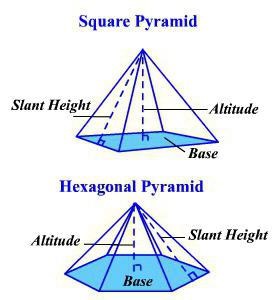
A tetraéder egy speciális esete, egy háromoldalú piramis. Minden élek egyenlő. Így kiderül egyszerűsített képlet újra:
Csonka gúla válik, amikor levágta a felső rész. Ezért, a mennyiség megegyezik a különbség a két piramisok: ami lenne ép, és a távoli tip. Ha van egy lehetőség, hogy megtanulják mind a alapja a piramis (S1 - nagyobb és S2 - kevesebb), célszerű, hogy egy képletet a mennyiség:
Henger, kúp és csonka
Ha kell számítani űrtartalomtól, akkor a képlet, meghatározott prizma. Néha kényelmes írni, hogy ebben a formában:
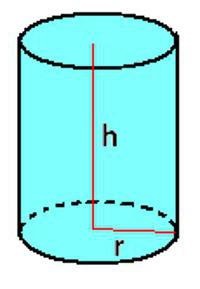
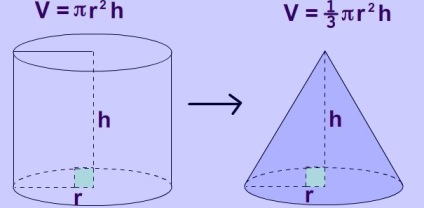
Valamivel bonyolultabb a helyzet a kúp. van egy képlet érte:
V = 1/3 π * r 2 * h. Ez nagyon hasonlít az egyik, hogy van megadva a henger, csak az érték csökken háromszor.
Csakúgy, mint egy csonka gúla, a helyzet nem könnyű egy kúp, amely két bázist. A képlet a kötet egy csonka kúp néz ki:
Golyó, szektorszegmensek
Ez a legnehezebb megjegyezhető formula. A kötet egy gömb ez így néz ki:
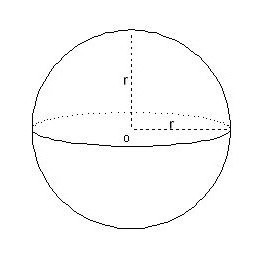
A problémák gyakran a kérdés, hogyan lehet kiszámítani a kötet egy gömb alakú szegmens - része a gömb, hiszen vágtunk párhuzamosan az átmérője. Ebben az esetben, az ilyen képlet jön a mentő:
V = π h 2 * (r - h / 3). Ez hozott H szegmens emelkedést, azaz azon a részen, amely sugara a labdát.
A szektor két részre oszlik: a kúp és a labdát szegmens. Tehát a definíció szerint ezek összege szervek. A képlet a transzformáció után a következő:
V = 2/3 πr 2 * h. Itt H és elevációval.
példák feladatok
Pro kötetek henger, gömb, és egy kúp
Feltételek: henger átmérője (1 test) egyenlő a magassága, az átmérője a labda (2 test) és a magassága a kúp (3 szerv); ellenőrizze az arányosság kötetek V1. V2. V3 = 3: 2: 1
Határozat. Először is meg kell rögzíteni három képletek kötetek. Aztán úgy vélik tartomány - fél átmérőjű. Azaz, a magassága egyenlő lesz kétszerese a sugár: h = 2r. Performing egyszerű helyettesítés kiderül, hogy a képlet a mennyiség lesz a forma:
V1 = 2 π R 3; V3 = 2/3 π r 3. A képlet a kötet egy gömb nem változik, mert a magasság nem jelenik meg benne.
Most, hogy írja le az összeget, és a csökkentés és 2π r 3. Kiderült, hogy a V1. V2. V3 = 1 2/3. 1/3. Ezek a számok könnyen vezethet utáni 3. 2. 1.
Feltételek: görögdinnye két sugara 15 és 20 cm; esznek jövedelmezőbb: az első négy vagy nyolc, a második?
Határozat. Ahhoz, hogy erre a kérdésre válaszolni, meg kell találnunk a térfogati aránya az alkatrészek, hogy megy minden görögdinnye. Figyelembe véve, hogy azok - a golyó, meg kell írni két képlet kötet. Akkor vegye figyelembe, hogy mind az első lesz csak a negyedik részben, a második - nyolcadik.
Továbbra is felvenni a térfogati aránya részek. Úgy fog kinézni:
(V1. 4) / (V2. 8) = (1/3 π r1 3) / (1/6 π r2 3). Miután az átalakulás csak egy töredéke (2 r1 3) / r2 3. behelyettesítése után a kapott értékeket, és kiszámításához a frakció 6750/8000. Ebből nyilvánvaló, hogy az első része a görögdinnye kisebb, mint a második.
Válasz. Nyereséges enni nyolcadik a görögdinnye egy 20 cm sugarú körben.
Feltételek: agyag piramis egy téglalap alakú bázissal 8H9 cm és magassága 9 cm; ugyanabból a darab agyagból készült kocka; amely egyenlő annak szélén?
Határozat. Ha jelöljük a része a betűk a téglalap, majd a terület a alapja a piramis számítjuk ki, hogy a termék. Ezután a képlet térfogata:
A képlet a kötet egy kocka van írva a fenti cikkben. Ez a két érték: V1 = V2. Továbbra is egyenlőségjelet tesznek a jobb oldalán képletek és végezze el a szükséges számításokat. Kiderült, hogy a szélén a kocka egyenlő 6 cm.
Feltételek: fiókos szükséges, hogy egy kapacitása 0,96 m 3 ismert szélessége és hossza - 1,2 méter és 0,8; mi legyen a magassága?
Határozat. Mivel az alap a paralelepipedon - egy téglalap, a területet úgy definiáljuk, mint a hosszúság (a) a szélessége (c). Ezért a képlet a hangerő így néz ki:
Belőle könnyű meghatározni a magasságot, elosztjuk a hangerőt a területen. Kiderült, hogy a magassága legyen egyenlő 1 m.
Válasz. A doboz magasságát egyenlő egy méter.