Geometriai módszerek a problémák megoldására
Az ingatlan az alapvető lineáris programozási feladatok kapcsolatos tulajdonságait konvex halmazok.
A pontok halmaza nevezett konvex, ha együtt bármely két pont tartalmaz domború, és azok tetszőleges kombinációja.
A geometriai e meghatározás értelmében az, hogy a beállított együtt a teljes tulajdonú önkényes pontok és az összekötő szakasz őket. Példák konvex halmazok egyenes vonalú szegmens, félsíkban, kör, gömb, kocka, fél-és mások.
Sarokpontjait konvex munkapont úgynevezett nem-konvex kombinációja két tetszőleges pont a készlet. Például derékszögű háromszög pontok a csúcsai, kör - pont köre, hogy a korlátot.
Sok a fő feladata a lineáris programozás tervek konvex (ha nem üres). Nem üres halmaza tervek nevezzük poliéder megoldásokat, és minden sarkából a poliéder pont megoldások - tetején.
Ha az alapvető probléma a lineáris programozás az optimális terv, a célfüggvény a probléma veszi a maximális értéket az egyik csúcsot a döntéseket. Ha a maximális értéket elérjük több vertex, az objektív függvény megkapja minden pontja a konvex lineáris kombinációja ezen csúcsok.
Egy nem üres halmaza tervek, az alapvető probléma a lineáris programozás képez konvex poliéder, minden csúcsa, amely meghatározza az alapvető tervet. Az egyik a referencia tervek (azaz, az egyik a csúcsai a poliéder megoldások) az objektív függvény egy maximális (feltételezve, hogy a funkció határolja felülről a sor tervek).
Csúcsai a döntéseket, amelyek az objektív függvény eléri a maximális értéket, akkor lehet találni elég egyszerű, ha a probléma a szokásos formában nem tartalmaz több mint két változó:
A kereszteződés fél-síkok által meghatározott egy lineáris egyenlőtlenségek nevezett oldatok (HR) rendszer, és ha megfelel a feltételeknek a nem-negativitás. ez az úgynevezett doménjét megvalósítható megoldásokat (SDT).
Ha a rendszer kompatibilis egyenlőtlenségeket, a terület a megvalósítható megoldásokat a probléma egy konvex halmaz, amely az úgynevezett egy sokszög megoldásokat. Az oldalán a sokszög fekszenek a sorokat, amelyek egyenleteket származnak az eredeti
rendszer korlátai helyett az egyenlőtlenség jele a pontos egyenlőségjel.
Megoldása lineáris programozási problémák geometriai eljárás magában foglalja a következő lépéseket.
1. A sík épült egyenes, amely egyenleteket kapjuk meg, hogy az egyenlőtlenség jele a korlátozások pontos egyenlőségjel.
2. Keresse meg a félig által meghatározott sík egyes korlátok a problémát.
3. Készítsen egy sokszög megoldásokat.
4. Készítsen egy vektor, amely mutatja az irányt, hogy növeli a célfüggvény.
5. építsünk kezdeti közvetlen célfüggvény és akkor mozog önmagával párhuzamosan az irányba, hogy a vektorba a szélsőséges sarokpontját a sokszög megoldásokat. Ennek eredményeként, a megállapítás a pont, ahol a cél a függvény feltételezi a maximális értéket, vagy több pontot az azonos legnagyobb értéke a célfüggvény optimális alternatíva, ha a start vonal összeolvad egyik oldalán a sokszög készítés, vagy set-top határtalan funkció egy sor terveket.
6. Határozza meg a pont koordinátáit a maximum funkciót és értékének kiszámításánál a célfüggvény ezen a ponton. A minimális érték a célfüggvény egy lineáris mozgást a kezdeti vonal ellentétes irányban a vektor.
Példa 1. Keresse meg a maximális és minimális lineáris függvény
Határozat. Készítünk egy sokszög, hogy sík (ábra. 1). Ehhez a egyenlőtlenségek rendszerének korlátozások és feltételek nemnegativitását változók egyenlőtlenség jelek váltja finom egyenlőségjel.
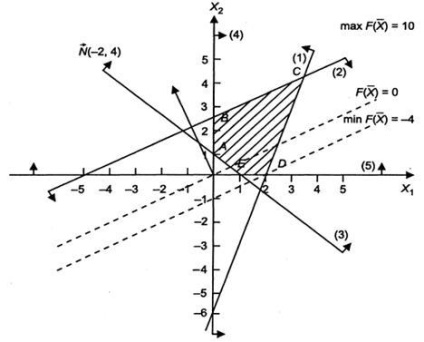
1. ábra építése megoldások sokszög
Beépített megfelelő rendszer, megtaláljuk a megfelelő félsíkban, és azok találkozásánál.
Solutions sokszög egy ötszög ABCDE pont, amelynek koordinátái kielégítik az alábbi egyenlőtlenségeket változók és nemnegativitását megszorítások a rendszer problémáját.
Ahhoz, hogy megtalálja a szélsőérték pontokat a kezdeti szerkezetet és az közvetlen vektort (-2, 4). Mozgó egyenesen az irányt a vektor, megtalálja a C pont, amelyben a kezdeti vonal feltételezi a helyzet a referencia-vonal. Következésképpen, a C pont objektív függvény van egy maximális értéke. Mivel C. pont kapott vonalak metszéspontjába 1
és 2-ből a rendszer, ha a koordinátái kielégítik az egyenleteket e sorokat:
Megoldása az egyenletrendszert, kapjuk: = 3,4; = 4,2; ahol megtaláljuk a maximális célfüggvény érték = (- 2) * 3.4 + 4 * 4,2 = 10.
A hipotézis, a kezdeti probléma párhuzamos egyenes vonal (2), mivel az együtthatók a változók. arányos (-2) / (- 1) = 4/2 = 2. Következésképpen, a kezdeti helyzetben a referencia egyenes vonalat a pont B, C, és bárhol a szegmens BC, amely azt feltételezi, hogy az azonos legnagyobb értéket. Ahhoz, hogy meghatározzuk a pont koordinátái B megoldja a rendszer két lineáris egyenletek:
A maximális érték a célfüggvény a ponton B egyenlő:
Írunk a készlet optimális megoldások lineáris kombinációja konvex sarkok szegmens BC pontok, ahol.
Behelyettesítve a koordinátákat a sarokpontok, kapjuk:
Behelyettesítve bármilyen érték 0 és 1 közötti, megkapjuk a koordinátáit a több szegmens BC pontok, amelyek mindegyike az objektív függvény feltételezi egy maximális érték egyenlő 10.
Ahhoz, hogy megtalálja a minimális érték a célfüggvény a probléma kezdeti lépés egyenesen ellentétes irányban a vektor. Kezdővonal feltételezi a helyzet a referencia-vonal a vertex D, ahol k = 2, = 0, és a minimális értékét az objektív függvény: = (- 2) * 2 + 4 * 0 = -4.
2. példa: Egy geometriai módszer megoldására lineáris programozási problémák példája a feladat, és a felépített modell üzleti vállalkozás, bemutatott Sec. 2.2.1. Mivel a modell csak két változót,
akkor ez a probléma megoldható egy geometriai módszerrel.
Construct a gépen (ábra. 1), egy sokszög az megvalósítható megoldásokat a probléma. Ehhez a egyenlőtlenségek rendszerének korlátozások egyenlőtlenség jelek helyére pontosan egyenlőség jelek:
Építésére kapott korlátozó közvetlen megtalálják a megfelelő felezési síkja megengedett a változók értékeit, majd a kereszteződés (1.).
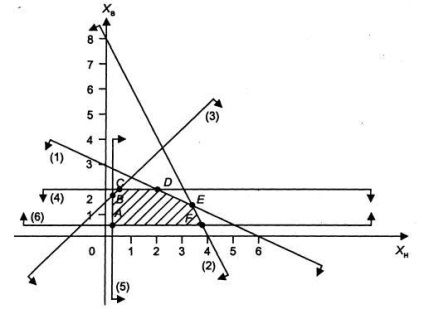
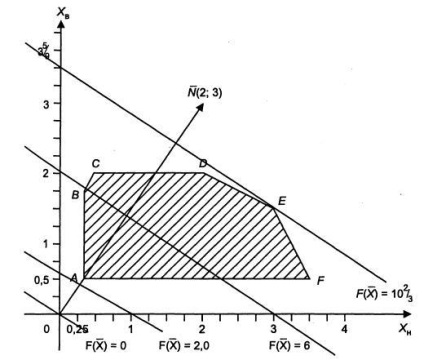
1. ábra Építőipari területének megvalósítható megoldásokat
Irány nyilak az egyes határvonal által meghatározott közvetlen szubsztitúciós a koordináta-egyenlőtlenség önkényesen kiválasztott pont, például (0, 0), és amikor az elégedettség a egyenlőtlenség a nyíl irányában célja ellenőrzőpont egyébként - éppen ellenkezőleg.
A kapott oldatot térben van egy sokszög ABCDEF.
Sarokmegoldások sokszög pontok az alábbi koordinátákat:
Egy (0,25; 0,5), B (0,25, 1,75), C (0,5, 2), D (2, 2), az E (3; 1), F (3,75 0,5).
Ahhoz, hogy megtalálja a minimális és maximális a célfüggvény és a kivitelezést egy kezdeti közvetlen vektor gradiens (2; 3) (2. ábra). Koordinátái a vektor lineáris együtthatók a célfüggvény változók. A konstrukció a grafikon a célfüggvény adott egy tetszőleges értéket .Ha = O, a vonal áthalad a származási. Az építéshez, beállítás = 1, megkapjuk a = -2/3, és k értéke 1, megkapjuk a = -3/2 (ábra. 2). Feltételezve = 6, azonos módon sorban megépíteni a célfüggvény.
Ekkor = 0,25 és = 0,5 határozzák meg a minimális érték = 2. Így, a grafikon össze egy sor párhuzamos vonallal (2. ábra)., Ahol A gradiens vektor (2, 3) jelzi a haladási irányt, a célfüggvény.
A maximális érték lesz ponton E. Mivel az E pontban kapjuk a vonalak metszéspontjába (1) és (2), akkor a koordinátarendszert opredeleniyaee megoldja az egyenletrendszert:
A maximális érték a célfüggvény
A célfüggvény metszi a tengelyt a ponton =. és azon a ponton = tengely.