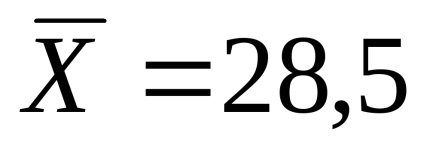Adatmetrikát „hajlandóság kockázat”

előző ◈ a következő

Kiszámítjuk az átlagos hajlam kockázat a kísérleti (I) és a kontroll (II) a következő csoportok:

;

.

Ezekből a számításokból kitűnik, hogy a minta átlagos hajlandóság kockára játékosok a kísérleti csoportban (

Adatmetrikát „hajlandóság kockázat”
) A magasabb, mint a kontroll csoportban, és véletlenszerűen kiválasztott emberek (
Adatmetrikát „hajlandóság kockázat”
).

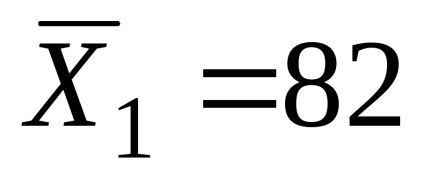
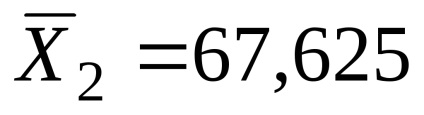
Mondhatjuk, hogy a kapott különbségek statisztikailag szignifikánsak, nem véletlen?

Válassza ki a kritériumokat, hogy ellenőrizze a tartalmát a hipotézist, hogy a játékosok kockázati étvágy magasabb, mint a véletlenszerűen kiválasztott emberek csoportja.

Annak tesztelésére, ilyen feltételezést - körülbelül azonos (különbség) átlagos értékek (szintek) a funkció két független minta - kínál több kritérium [2], például:

 Student paraméteres teszt összehasonlító eszközt;

 nemparaméteres teszt Rosenbaum;

 paraméteres Mann - Whitney.

Mivel az egyes független csoport alanyainak egy minta kis térfogatú. és

Adatmetrikát „hajlandóság kockázat”
(
Adatmetrikát „hajlandóság kockázat”
) Az összehasonlítás általános átlagok ebben az esetben a legtöbb helyes lenne, hogy használja a nem-paraméteres Mann - Whitney.

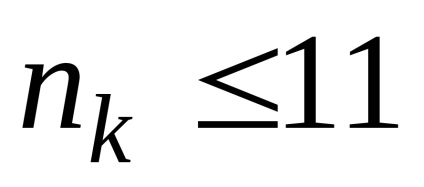
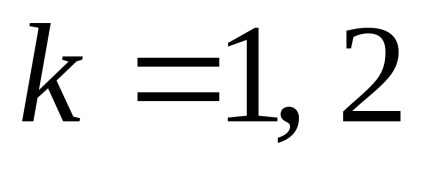
Megfogalmazzuk statisztikai hipotéziseket.

Adatmetrikát „hajlandóság kockázat”
: Különbség a két csoport alanyainak szintjén kockázati étvágy, véletlenszerű (hivatalosan:
Adatmetrikát „hajlandóság kockázat”
);

Adatmetrikát „hajlandóság kockázat”
: A a mutató szintje „kockázati étvágy” a kísérleti csoportban a játékosok szignifikánsan magasabb volt, mint a kontroll csoportban a véletlenszerűen kiválasztott emberek (formálisan:
Adatmetrikát „hajlandóság kockázat”
 az esetben célja hipotézisek).

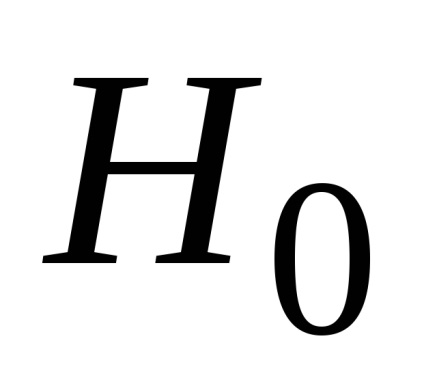
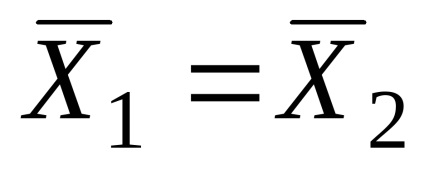
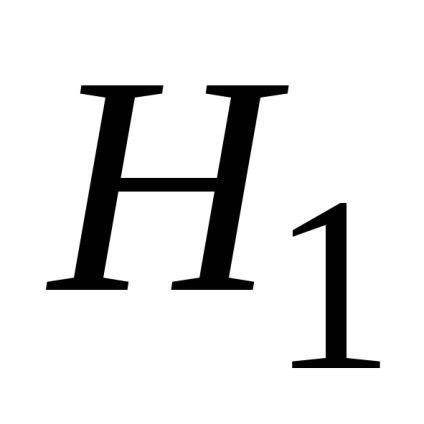
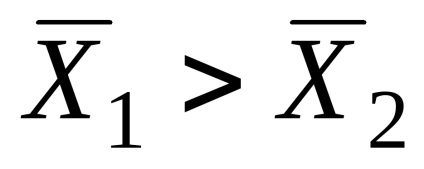
A számításhoz az empirikus statisztikai értékek

Adatmetrikát „hajlandóság kockázat”
Mann - Whitney rank a szükséges megjegyzésekkel két csoport személynek egyetlen mintában.

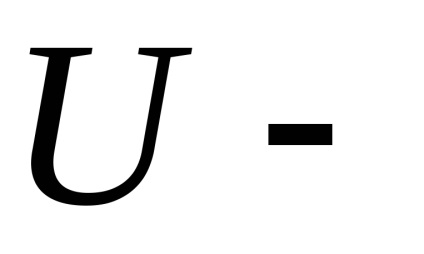
a rangsor eljárást két lépésben végezzük:

rendelési megfigyelési adatok, például emelkedő sorrendben;

a tényleges rangsorban, azaz tulajdonított rendezett adatok sorszámait (soraiban).

Továbbá, ellenőrzi a pontossága a rangsor: a tényleges kapott összeg soraiban egyenlőnek kell lennie a számított elméleti számított képlet szerint

Adatmetrikát „hajlandóság kockázat”
, ahol
Adatmetrikát „hajlandóság kockázat”
minta mérete.

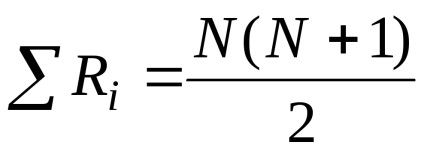
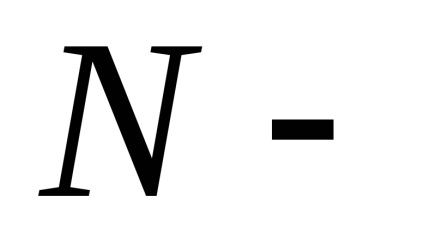
A kényelem kiszámításának rangsorolás és rangösszeg minden csoportban így a becsült táblázat (lásd. Táblázat. 1.2).

Counting rangösszeg kísérleti (I) és a kontroll (II) minták

I. A kísérleti csoport

(

Adatmetrikát „hajlandóság kockázat”
)

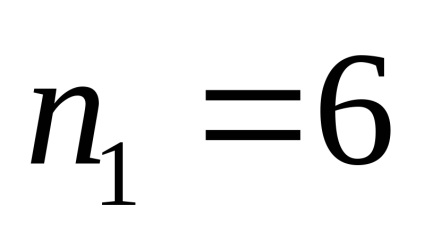
Ellenőrzése rangsorolás:

a tényleges összege a soraiban;

Az elméleti összegét a soraiban

().

Az igazi összege a soraiban egybeesnek elméletileg egyenlő 105, így a rangsorban megfelelően végzik.

Most lehet számítani az értékét empirikus statisztikai

Adatmetrikát „hajlandóság kockázat”
Mann - Whitney képlet,

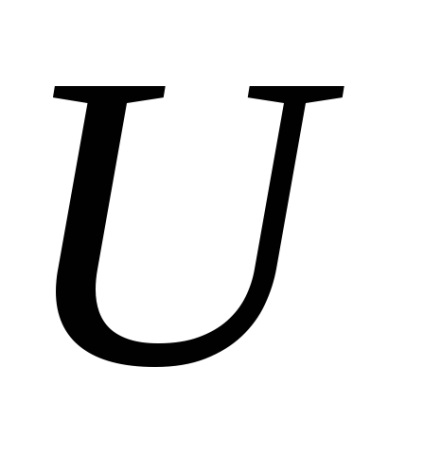
ahol a nagyobb a két kapott rank sum;

Adatmetrikát „hajlandóság kockázat”
A minta mérete összegével soraiban bólshey
Adatmetrikát „hajlandóság kockázat”
.

.

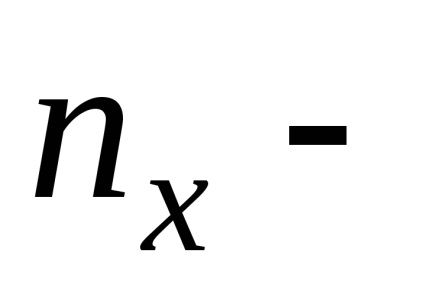
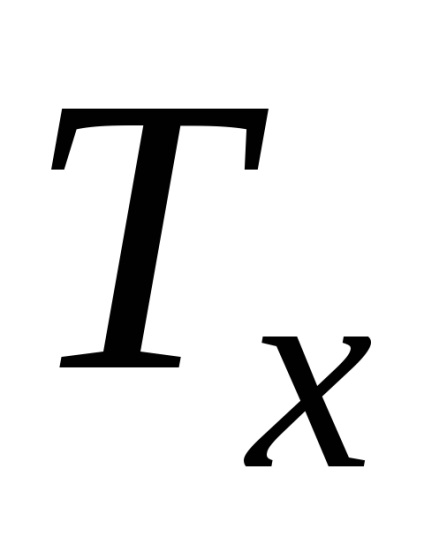
A táblázat a kritikus értékek

Adatmetrikát „hajlandóság kockázat”
Mann - Whitney tesztet az irányított hipotézist [2, 3], definiálunk:

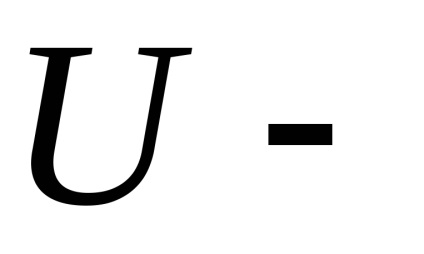
. ezért a hipotézis

Adatmetrikát „hajlandóság kockázat”
(
Adatmetrikát „hajlandóság kockázat”
) Nincs különbség a szint a attribútum két független minta ellen irányul alternatívák
Adatmetrikát „hajlandóság kockázat”
(
Adatmetrikát „hajlandóság kockázat”
) Megléte jelentős különbség a jellemző szintet lehet utasítani, ha
Adatmetrikát „hajlandóság kockázat”
.

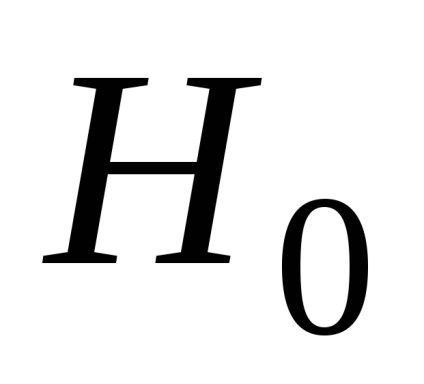
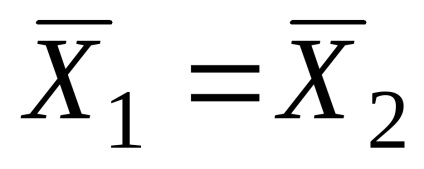
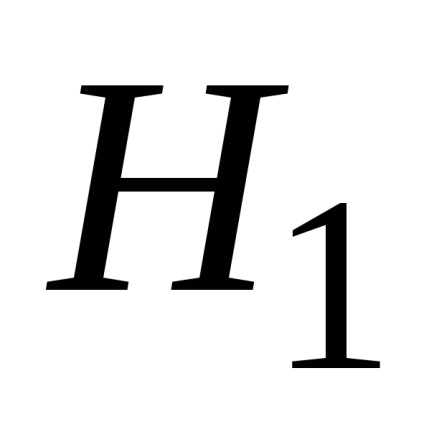
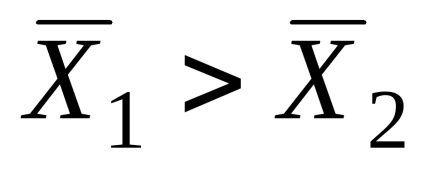
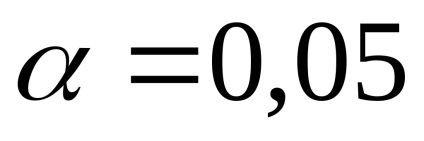
Ezért az a következtetés, hogy a tanulmány az adatok összhangban vannak a hipotézist

Adatmetrikát „hajlandóság kockázat”
: Egy csoport játékosok értékét tükröző index a kockázatvállalási hajlandóság, jelentősen magasabb, mint a csoport véletlenszerűen kiválasztott emberek.

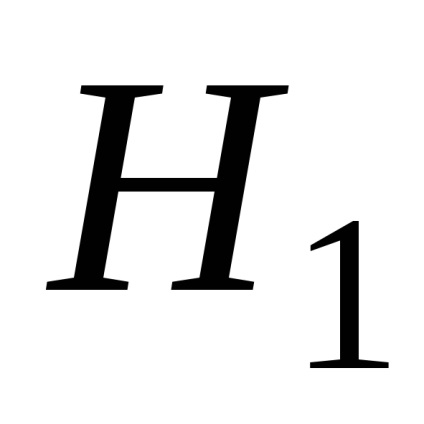
2. példa - meghatározása csatlakozó tömítettségét (korrelációs vizsgálat).

Adatmetrikát „hajlandóság kockázat”
soglasovannost (korreláció) csoportban hierarchia hiányzik;

Adatmetrikát „hajlandóság kockázat”
soglasovannost (korreláció) a csoport hierarchiájában statisztikailag szignifikáns, nem véletlen.

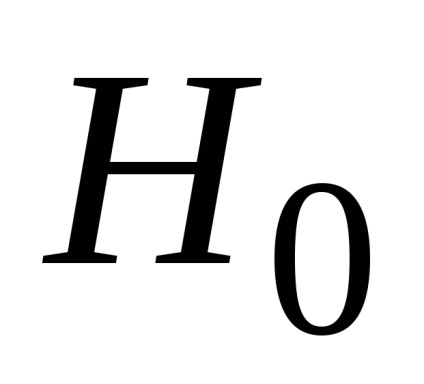
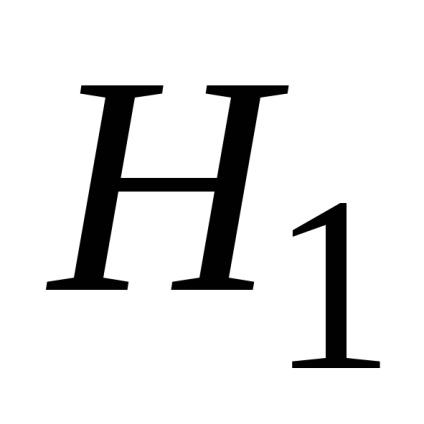
Fennállásának megállapítása koherencia (kapcsolat), és megbecsüli a feszességét csoportok közötti hierarchia (fokozat) lehet használni a Spearman korrelációs együttható

Adatmetrikát „hajlandóság kockázat”
[1]:

.

Kritikus értékek Spearman korrelációs együttható

Adatmetrikát „hajlandóság kockázat”
függően a minta méretét
Adatmetrikát „hajlandóság kockázat”
és a szignifikanciaszint
Adatmetrikát „hajlandóság kockázat”
egyenlő [1, 3]:

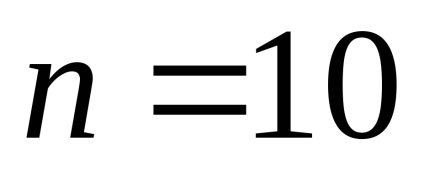
3. példa - Tesztelés Statisztikai hipotézisek vizsgálata és korreláció.

 átlagos pontszám (pontszám) eredményeit két év tanulmány az egyetemen;

 Programozási ismeretek (teszt: 21 kérdés, 30 perc);

Az eredményeket a 3.1 táblázatban.

A kutatók érdekel a kérdés:

hogy a diákok megfelelnek MF KemSU ismert szokásos CAT teszt (IQ) az egyetemi hallgatók, a 28 pontot?

Mi az arány a mért paraméterek szintje a lányok és fiúk?

Van-e összefüggés a mért paraméterek?

1) A kérdés megválaszolásához mindenekelőtt a kutatás - akár MF diákok a megfelelő KemSU normál CAT teszt (IQ) az egyetemi hallgatók, a 28 pont neobhodimo kell számítani az átlagos mintaérték urovnyaIQstudentov MF KemSU és válassza ki a megfelelő statisztikai próba.

Mid IQstudentov MF KemSU

Adatmetrikát „hajlandóság kockázat”
(Lásd. 3.2 táblázat.).

Kapcsolódó cikkek

előző ◈ a következő