maximalizációt - studopediya
Két megközelítés lehet használni, hogy megoldja a maximalizálása problémákat.
Podhod1. Conversion maximalizációt egy ekvivalens probléma minimalizálása objektív függvény szorozva -1, majd alkalmazása a szimplex módszer, hogy minimalizálja a problémát.
Approach 2. Mint a fentiekből kiderül, a relatív értékelési sor pj változását reprezentálja az f célfüggvényt csökkenő nonground változó eggyel. A negatív együtthatót PJ vonal jelzi a növekedésével csökken f nonground megfelelő változó.
Tehát, hogy maximalizálja a feladatokat kell vinni a alapján nem bázisos változó xj pozitív pj. mivel azok javítják a célfüggvényt. Ha minden együttható PJ sorban negatív vagy nulla, a jelenlegi megoldás optimális.
Példa 6.9. Problémák simplex - Eljárás probléma:
Határozat. A rendszer segítségével a további nem-negatív változók lépéshez egyenletrendszert. Ebben az esetben minden további változók bevezetni a „+”, mint az összes egyenlőtlenségek a forma „”
Megkapjuk a rendszer korlátai formájában:
És a T E R ációk 1.
Feltételezve, hogy az egyenletek (6.37) szabad változók x1. x2 nullával egyenlő, találunk. . . . azaz alapvető megoldás X 0 = (0; 0; 18; 16; 5; 21). Mivel az összes alapvető változók a pozitív x 0, ez a bázis a megoldás elfogadható (sarokpont) és a nem-degenerált. A megközelítés 1, megyünk a minimalizálás probléma
Egyenletek alkalmazásával (6,35) és a (6.36) össze Simplex - táblázat megfelelő sarokpont x 0:
A 4. igénypont szerinti ellenőrzést algoritmust optimalitást kritériumot. Az utolsó sorban, vannak negatív tényezők. Válasszon a számukra leginkább mod (-3); amely lehetővé teszi a második oszlopban a változó x2 megy át a fő (az oszlop nyíllal jelölve). Az 5. igénypont szerinti és megtaláljuk a becsült kapcsolatot. A harmadik sorban a felbontás (jelzett vízszintes nyíl). Metszéspontjában megoldása a sor és oszlop kell tartóelem (keretezni).
És t e r á n 2 Építés szabálytáblázatok 6. igénypont algoritmus (fülre. 6.10). Az új alapot a fő változók.
A optimalitás kritérium nem találtak újra. Most az első oszlop lehetővé teszi; x1 - az átmenet a fő ,; Az első sorban felbontás - a tartóelem.
Simplex-asztal sarokpontjait X1
És t e r á n 3. Az új szimplex tábla formájában (fülre. 6.11).
Simplex táblázat sarokpont x 2
És ebben az időben, az optimum kritérium nem teljesül; a második oszlop és a második sorban - lehetővé teszi - egy tartóelemet.
És t e r á n 4. Menj a táblázat 6.12.
Simplex táblázat sarokpont x 3
Optimalitási kritériumként van kialakítva, akkor f * = f (x) = 24, egy optimális bázikus oldat x * = (6,4,0,0,1,3).
Grafikus probléma megoldása ábrán látható. 6.10, ami azt mutatja, hogy x = (6, 4), és f * = f (x) = 24.
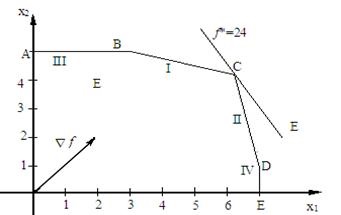
Ábra. 6.10. Grafikus megoldás a problémára 6,19