Munka adatszerkezeteket C és python 6. rész
Stay tuned a közelgő cikkek ebben a sorozatban.
Ez a tartalom egy sorozat része: Work adatstruktúrákkal C és Python
Stay tuned a közelgő cikkek ebben a sorozatban.
A bináris (binary) fák az egyik legnépszerűbb változat az adatstruktúra, hiszen széles körben használják a keresési algoritmusok és egyéb számítási feladatok. Ez a cikk lesz szó a fő jellemzői a bináris fák, és a különböző műveleteket végezni velük.
Mint rendesen, ráadásul elméleti szempontból: a besorolás a bináris fák és standard technikák manipulálására, a cikk néhány példa a gyakorlati megvalósítása algoritmusok manipulálására bináris fa C és Python nyelven.
Osztályozása bináris fák
Mielőtt rátérünk a különböző típusú bináris fák, akkor kap, az általános besorolását a kereső algoritmusok.
Abban az esetben, lineáris keresés a kívánt elemet összehasonlítjuk minden bejegyzést a listából során egymást követő iterációk. A sebesség a keresési méretétől függ a lista: egy listát a több, annál kisebb a sebesség, azaz sebessége fordítottan arányos a méret a listán. Növeli a sebességet a keresési lehet, ha az előre rendezze a listát. Ebben az esetben nem kell folytatni a keresést, ha a kívánt elem még nem találták meg, és az elemek a lista még hosszabb lesz szükség.
Egy rendezett lista van egy hatékonyabb algoritmus. Az elején a keresési össze kell hasonlítani a kívánt számú tétel, amely a középső már rendezett lista. Ha a középső elem meghaladja a szükséges számot, majd a kívánt elem található, a bal felét. Ellenkező esetben - a jobb oldalon. Ezután összehasonlítást végzünk egy számot, amely szükséges a középső felében. És így tovább, amíg, amíg a kívánt szám megtalálható. Ez a keresési nevezzük bináris. és ő nyilvánvalóan gyorsabb, mint lineáris. A szükséges számú körzetek a lista álló n elem fél, úgynevezett logaritmusa n a 2 alaptag bináris keresés algoritmus rend O (log) bázis 2.
Ugyanakkor a hagyományos kapcsolt listák nem nagyon alkalmas bináris keresés, és itt jön a támogatás egy bináris fa, amelynek egyik példája az 1. ábrán látható.
1. ábra: Példa egy bináris fa
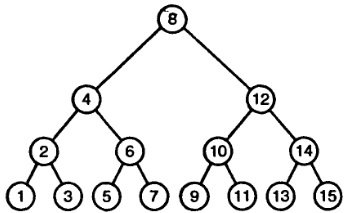

Általában minden csúcs a fában lehet korlátlan számú gyermek csomópontok. bináris fa Eltérően más típusú fák, hogy minden csomópont ott lehet kettőnél több gyermek csomópontok. Hagyományos bináris fa - egy szerkezet, amely a csomópontok, amelyek mindegyike tartalmaz egy bizonyos értéket, valamint rámutatnak a bal és a jobb részfa. Az egyik vagy mindkét mutatót a részfákat lehet NULL. Bináris fák, valamint a kapcsolódó listák rekurzív struktúrákat.
A 2. ábra a bináris fák, amelyek mindegyike ugyanazon csomópontok halmaza, de különböző sorrendben azok szekvencia. Az utóbbi esetben, a fa fajul egy láncolt lista.
2. ábra: A különböző megvalósításai azonos bináris fa
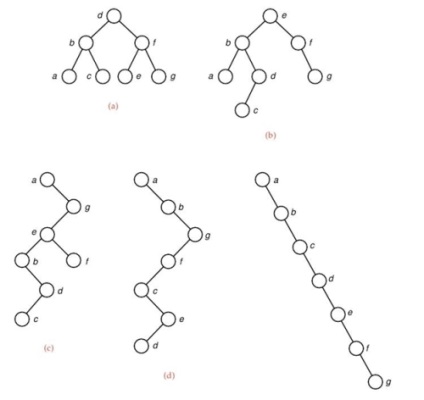

A következő típusú bináris fa:
- teljes bináris fa - minden egyes csomóponthoz, kivéve levél két gyermek csomópontok;
- tökéletes bináris fa - ez egy teljes bináris fa, amelynek során valamennyi levelek ugyanabban a magasságban;
- kiegyensúlyozott bináris fa - ez bináris fa, ahol a magassága 2 részfák minden egyes csomóponthoz nem többel, mint 1. A a fa mélysége van kiszámítva, mint a logaritmus log (n), ahol n - az összes csomópont;
- degenerált fa - egy fa, amely minden csomópont csak egy gyermek csomópont, ez valójában egy láncolt lista;
- bináris kereső fába (BST) - bináris fa, ahol minden csomópont állapot: az összes csomópontot a bal részfa kevesebb, és az összes csomópont a jobb részfa a csomópont hosszabb.
útvonalak
Path (angol útját.) - a távolság a gyökér, hogy egy adott csomópont. A kiterjesztett bináris fa, minden egyes pálya végén egy lapot. Ha a szám kijelölt S. elhagyja és a számos más csomópontok kijelölt N., hogy kielégíti a:
azaz hosszabb levelek számát a fa az egyik nagyobb, mint a több NElistev (csomópontok, amelyek gyermek csomópontok).
Ha az útvonal a gyökér-csomópontból az levél kijelölt, mint a külső útvonalat, és az utat a gyökér-csomópontból kell kijelölni NElista belső útját, akkor az összeg az összes külső pályák a fa 3. ábrán látható jelentése:
és belföldi útvonalakon egyenlő lesz az összege:
majd lesz a képlet:
ahol n - a számos belső csomópontok (NElistev).
3. ábra Példa kiterjesztett fa
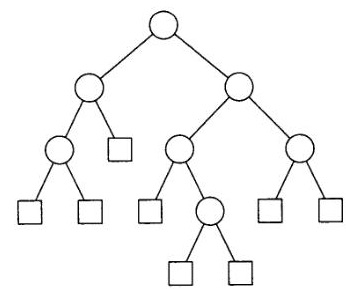

Tegyük fel, hogy a következő sor a levelek:
Akkor tudjuk megfogalmazni a következő feladatokat látja el:
- építeni egy bináris fát úgy, hogy az összeg a pályák minimális volt, mivel csökkenti a számítási időt különböző algoritmusok.
- építeni egy teljes bináris fa kitágul, hogy az összeg a termékek utak a gyökér csomóponttól a levelek a levél csomópont értéke minimális volt.
David Huffman (David Huffman) javasolt egy algoritmust a feladat megoldására, amelyben a két legalacsonyabb lap van kiválasztva, és hozzá minden lépésben, amint az 1. lista, amely ahhoz vezet, hogy a fa a 4. ábrán látható.
1. lista példa Huffman algoritmus
4. ábra: a bináris fa által épített Huffman
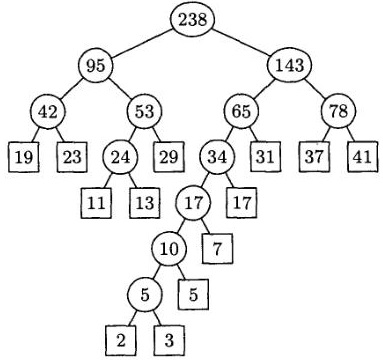

Huffman-kód
Huffman-kód - a használt algoritmus az adatok tömörítésére. Tegyük fel, hogy néhány eredeti szöveges üzenetet, amely 5 jelek: a, b, c, d, e. és minden karakter megvan a saját jelentése:
Kell kódolni ezt az üzenetet a 0 és az 1 úgy, hogy a méret a keletkező karakterlánc minimális volt. Az alábbi táblázat egy példát mutat a karakterkódolást ezt az üzenetet:
Ha üzenet titkosítása kód használatával bcd №1, kapsz - 001010011. A №2 kód nem ugyanaz, de az így kapott szöveget rövidebb - 1.101.001.
Most már megfogalmazni a probléma maga: ez kell választani egy ilyen titkosítási algoritmus, ahol a titkosított szöveg hossza minimális lesz.
Egy első megvalósításban minden karaktert adtak 3 karakter, és a második verzió - 2.2, de még mindig rövidebb lehet tenni, hogy egy tényező 2,15. Ezt használja a Huffman algoritmus, melyben a 2 szimbólumok veszik a legalacsonyabb frekvencia, és összekapcsolják a két gyermek csomópontok.
Algoritmus sorban álló 5 karakter a következőképpen valósul. Az első lépésben a két karakter együtt a - és d. mint amelynek a legalacsonyabb frekvenciától. A második, mint a szülő adunk C szimbólum. A harmadik lépésben hozzáadjuk az e karakter. és a végén - a szimbólum b. Az eredmény az alábbi kódot:
A magasság egy bináris fa
Annak megállapításához, a fa magasságát kell menni a gyökér a bal részfa az első, majd a jobb oldalon, összehasonlítani a két magasság, és válaszd a maximális értéket. Ne felejtsük el, hogy hozzáadott értéket a kapott egység (gyökér elem). 2. kódrészlet a rekurzív függvény ezt a feladatot.
2. lista meghatározása fa magassága - rekurzív végrehajtását C
„Mirror” tükrözi a bináris fa
Amikor a két fák tükörképei egymásnak, azt mondják, hogy ők szimmetrikus. Ahhoz, hogy „tükör” példányt a fa algoritmust alkalmazzuk, mint a 3. listában Először ellenőrizze a jelenlétét a gyökér a fa a gyermek csomópontok, és ha ezek a helyek, azok felcserélődnek. Ezután ugyanazt a lépéseket ismételjük rekurzívan a bal és a jobb oldali gyermek csomópontok. Ha csak egy gyerek, akkor lépni egy szinttel a fa alá, és tovább.
3. lista Fordított fa - rekurzív végrehajtását C
csomópont egy bináris fa keresés
Hogy keressen egy csomópont egy bináris fa foglalt értékeknek, akkor használhatja keresési funkciót. Látható a 4. listában:
4. lista Keresés a fában - rekurzív végrehajtását C
A szélessége egy bináris fa
A fa alatt szélességét értjük a maximális számú csomópontok, amelyek székhelye ugyanabban a magasságban. Annak megállapításához, a szélessége a fa, csak hogy adjunk egy számlálót, a már tárgyalt algoritmus meghatározására a fa magasságát.
5. lista szélességének meghatározása a fa - rekurzív végrehajtását C
A csomópontok száma bináris fa
Számoljuk ki a csomópontok száma a bináris fa is lehet a rekurziót.
Listing 6. A számítás a csomópontok száma a fa - rekurzív végrehajtását C
Összehasonlítás bináris fák
Annak eldöntésére, hogy két különböző gyufát, akkor az algoritmus 7. listán.
Listing 7. Összehasonlítás egy bináris fa - rekurzív végrehajtását C
következtetés
Ez a cikk már készült bináris osztályozási fák és úgy algoritmusok alapművelet végrehajtására: meghatározása szélessége és magassága a fa, visszaverődés fa és keressen benne egy bizonyos eleme. Szintén Huffman algoritmus ítélték, amelyet fel lehet használni építésére hosszabb fát, és ennek eredményeként, a kódoló információkat.
Letölthető Resources
Kapcsolódó témák
- Munka adatszerkezeteket C és Python nyelven. 1. rész.
- Munka adatszerkezeteket C és Python nyelven. 2. rész.
- Munka adatszerkezeteket C és Python nyelven. 3. rész.
- Munka adatszerkezeteket C és Python nyelven. 4. rész.
- Munka adatszerkezeteket C és Python nyelven. 5. rész.
- Munka adatszerkezeteket C és Python nyelven. 6. rész.