Axis természetes triéder Frenet
Meghatározása a természetes triéder Frenet. Az előrejelzések a sebesség és a gyorsulás egy pont a tengelye körül. Példa meghatározó egység vektorok természetes triéder.
A „kinematikája az anyag pont” oldal, megállapítottuk, hogy a sebességvektor a pont irányul érintőlegesen az utat. gyorsulásvektor fekszik a simuló síkban, és ez lehet bontani két komponenst. Az egyik komponens mentén irányul érintő a pályához. A második komponens merőleges a érintőleges az oldalán a pillanatnyi görbületi középpontja a pálya.
Bizonyos esetekben célszerű bevezetni a koordináta-rendszer kapcsolódó aktuális pozícióját a lényeg. Vegyünk egy pont egy bizonyos időben. Úgy gondoljuk, hogy tudjuk, hogy a pályáját a mozgás. Felhívjuk a három vonalon - pályaérintőre, fő normál és binormal. Fő normál merőleges érintője és irányul a pillanatnyi görbületi középpontja a pálya. Binormal merőleges az érintő és a normális haza. Úgy döntünk, egy koordináta-rendszert és annak eredete a ponton és tengelyek mentén vannak ezeken a vonalakon. Ez a koordináta-rendszer úgynevezett természetes triéder Frenet. A tengelye Ebben a koordinátarendszerben az úgynevezett természetes triéder tengely.
Horta természetes triéder
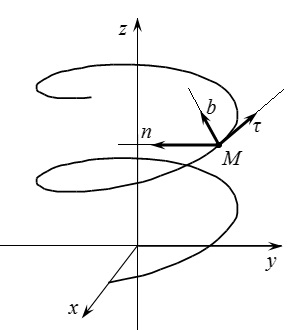
Let. és - az egység vektorok irányított mentén érintő, a fő normális és binormals a röppálya, ill. Ezek a vektorok a készülék vektorok a választott koordinátarendszer egység vektorok vagy természetes triéder. Azt a kérdést, a választás az irányt ezen vektorok.
Vektor mentén irányul érintő a pályához. Ezért lehetséges, hogy válasszon két egymással ellentétes irányban. A legegyszerűbb módja - mentén irányul sebességvektor a pont. majd
.
Azonban ez nem mindig lehetséges. Vannak esetek, amikor a pálya a mozgás előre ismert, és a sebesség - nem. Például, egy olyan ponton halad a csúszda mentén egy merev test az intézkedés alapján külső erők. Ilyen esetekben, a vektor irányát van kiválasztva előre. Például az irányba növekvő ív koordinátákat.
Az irány az egység vektor a fő normál egyedülállóan meghatározott. Ő merőlegesen. az irányt pillanatnyi görbületi középpontja a pálya.
Binormals vektor merőleges a vektorokat, és így a három vektorok. alkotnak egy jobbkezes koordináta-rendszerben:
.
Sebesség és gyorsulás szempontjából a Frenet triéder
Úgy véljük, hogy az irányt a vektor egybeesik a sebességvektor pontokat. Aztán alkalmazni a képlet, hogy mi hozta a „kinematikája az anyagi pont” oldalon.
Azaz, a természetes triéder a orts. sebesség az egyik komponens:
.
megegyezik a sebességgel a modul. Más szóval, a modulusa a sebesség - egy vetülete a sebességvektor tengelyére természetes triéder. A kiemelkedések a sebességvektor a triéder és a tengelyen nulla.
Gyorsítás két részből áll:
.
Ezek a komponensek érintő és a normális gyorsulás:
;
.
Ez normális és a tangenciális gyorsítási - a vetülete a gyorsulás vektor a tengelyen és a természetes triéder. A vetítés a gyorsulás vektor a nulla tengelyt.
Hogyan állapítható meg, a természetes tengelye triéder
Továbbá hisszük, hogy van egy rögzített koordináta-rendszerben. A anyagi pont mozgásban van. Szükséges, hogy megtalálják a tengelye a természetes háromszögletű. Ez az, hogy meghatározza a vetülete egység vektorok. és egy koordináta-rendszerben.
Képesti mozgását összehangolják és a vektor hozzárendelési módszerek
Koordinálása és vektor hozzárendelése módszerek a pont, a képletek meghatározására alapján vektorok látható „Kinematika anyagi pont” oldal. A „koordináta meghatározásának módját mozgását egy pont” szétszerelt egy példa számítási vektorok komponenseket.
Azaz, hogy meghatározza az egység vektorok természetes triéder, meg kell találni az összetevők sebesség vektorok és normál gyorsulás. a következő képlet alkalmazásával:
;
;
;
.
Ezután határozza meg az egység vektorok természetes triéder:
;
;
.
A természetes módon mozgás feladat
A természetes módon meghatározó a mozgását egy pont, tudjuk, hogy a pályája a mozgás. Ezért a mi feladatunk - az ismert pályája határozza meg a készülék vektorok természetes triéder. Ha az elérési út egy egyszerű mértani alakzat, például kört, majd meghatározza vektorok. és lehet geometriailag.
Általában a bonyolultabb esetben szükség van, hogy bemutassa a röppálya egyenletet paraméteres alakban. Ehhez adja meg a paramétert. Ezt meg lehet tenni sok szempontból. Ezért kívánatos, hogy válassza ki a legmegfelelőbb képviselete.
Tegyük fel például, a pályáját a mozgás egy ellipszis a síkban.
.
A legkényelmesebb parametrikus reprezentáció alkalmazásával lehet előállítani trigonometrikus képlet:
.
Ekkor az egyenlet az útvonal a következő:
Itt - opciót.
Nem ez az egyetlen módja egy parametrikus reprezentáció. Akkor például az egyenlet megoldásához az ellipszis relatív.
.
Alkalmazása a képlet, akkor kap egy másik parametrikus reprezentáció:
Továbbá feltételezzük, hogy ezek paraméteres egyenletek a mozgás egy anyagi pont, ahol a paraméter szerepet tölt be az idő. Ezután, hogy meghatározza a triéder tengelyekkel, akkor lehetséges, hogy alkalmazni a használt képlet a vektor és módszerek koordinálja mozgását feladat. Számított így, a sebesség és a gyorsulás függ a kiválasztott paraméter képviseletét. Azonban, a geometriai jellemzői a pálya, mint például egység vektorok. és a görbületi sugara pályákat nem függenek a kiválasztott paraméter ábrájának.
Tehát, hogy megtalálják a készüléket vektorok természetes triéder előre meghatározott úton mozgást. szükséges bemutatni az egyenlet pálya paraméteres formában és alkalmazni egy általános képletű a folyamatban használt koordináta mozgás feladat.
Példa meghatározó egység vektorok természetes triéder
Találja a készüléket vektorok tengelyek mentén a természetes triéder, és a görbületi sugara a pálya, egy hengeres spirál bázissal sugara és a menetemelkedés.
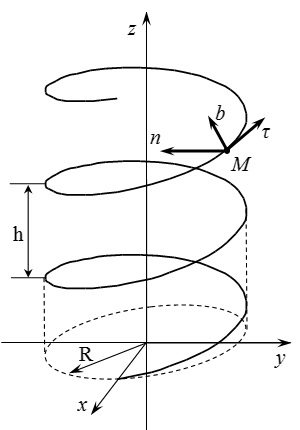
Úgy döntünk, egy koordináta-rendszert. Axis mentén spirál tengely. Ekkor az egyenlet a vonal is képviselteti magát a következő paraméteres alakja:
(1)
Itt - opció;. Ha vesszük a vetülete a vonal pont a síkon. majd - közötti szög a tengely és a nyúlvány. A növekedést az. és pont koordinátái visszakerül az eredeti helyére, és a koordináta nőtt.
Azt feltételezzük, hogy (1) egyenlet írja le a mozgását egy pont spirális irányba. Mi határozza meg a kinematikai mennyiségek ilyen mozgásra.
Differenciálás (1) egyenlet. Találunk a komponensek a sebességvektor:
;
;
.
sebesség négyzete:
.
fordulatszámú készülék:
.
Az egység irányába mutató vektor érintő a pálya:
.
Differenciálása a komponensek a sebességvektor. Megtaláljuk a komponenseket a gyorsulási vektor:
;
;
.
Tangenciális gyorsulás - egy vetülete az irányt a gyorsulás vektor.
Ez az eredmény nyerhető egy egyszerűbb módon. Erre a célra figyelmét, hogy a sebesség független a modul és alkalmazza a képlet:
.
Vector tangenciális gyorsulás:
.
Vektor normál gyorsulás:
A tér a normál gyorsulásvektor:
.
Modul normál gyorsulásvektor:
.
A görbületi sugár a pálya:
.
Az egység vektort az irányt a fő normális, hogy a pálya:
.
Az egység irányába mutató vektor binormals: