A10 vizsga számítástechnika
Továbbra is felkészüljenek a vizsgára a számítástechnika és most úgy a problémák megoldását a típus A10.
Problémák az ilyen típusú meglehetősen bonyolult. Megközelítés a problémák velük, nem tudván, az alapokat a logika nem éri meg. Ezért azt javasoljuk, hogy olvassa el a kötőszó. szétválás. vonzata.
A számú vonal két szegmens: P = [1, 39] és Q = [23, 58].
Válasszunk a kínált szegmensek egy szegmens A, amely egy logikai kifejezés
((X ∈ P) → ¬ (x ∈ Q)) → ¬ (x ∈ A)
azonosan igaz, azaz az 1 értéket bármely értéke az x változó.
1) [5, 20] 2) [25, 35] 3) [40, 55] 4) [20, 40]
Az egyszerűség kedvéért jelöljük az egyszerű nyilatkozatok nagybetűvel (címe szegmens):
Átírjuk a kifejezést egy sokkal kényelmesebb formában:
10. feladat USE Informatika
Most egy rövid kitérőt a vonzata. A következmény lehet kifejezni diszjunkció és negáció így:
Disclosure hallgatólagosan negáció és a diszjunkció
Ez egy nagyon fontos szabály, és meg kell emlékezni.
Most átírhatjuk a nyilatkozatot, és távol a következményei:
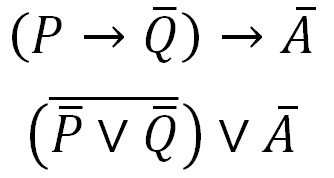
Hogy egyszerűsítse a kifejezést zárójelben használja a törvény de Morgan (második kép)
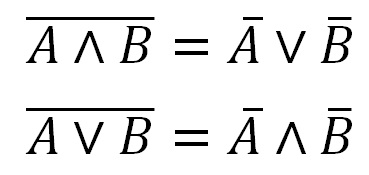
Törvények De Morgan
Ennek eredményeként megkapjuk
Törvény alkalmazása kettős tagadás megkapjuk a végleges kimutatás, amellyel fogunk dolgozni. Igen, ez még nem minden
Most, ne feledjük, hogy a nyilatkozatok - olyan intervallum, és megjeleníti azokat egy koordináta tengelyen.
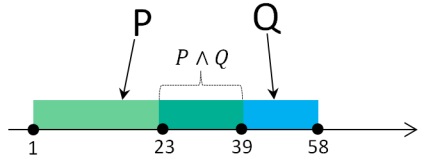
A feladat ütemezését
Elemezzük a menetrend, és a végleges kimutatást. A végleges kimutatást igaznak kell lennie minden olyan x értéke a probléma állapotban. Az utolsó állítás van egy kifejezés zárójelben és inverzió diszjunkciós A csatlakoznak. Diszjunkciót igaz, ha legalább az egyik vagy mindkét állítás igaz. Így a végleges kimutatás lesz igaz, ha bármilyen kifejezés zárójelben igaz, vagy a tagadása A igaz, vagy mindkét kifejezés igaz (zárójelben a tagadása A). A kifejezés zárójelben - egy együttes, és ez csak akkor igaz, ha mindkét állítás igaz. E. Ha az x tartozik az intervallum [23, 39] A végső állítás igaz. Ellenkező esetben a megnyilatkozás hamis, akkor a tagadás A igaznak kell lennie. Racsmotrim, ha ez így is lesz.
Az elején úgy döntöttünk, hogy a nyilatkozat A azt jelenti, hogy x ∈ A. Mivel ez már a tagadás tagadása A azt jelenti, hogy x ∉ A, és így az x pontban kell tartozniuk a tartomány [-∞, 23] vagy [39 , + ∞]. Továbbra is találni egy szegmensének, amely kiterjed a tartomány [23, 39] (mint már azt a tagadás, akkor előbb-utóbb megkapjuk a kívánt tartományon belül). E. Left koordinálja a szegmens nagyobbnak kell lennie, vagy egyenlő, mint 23, és a jobb oldali kisebb vagy egyenlő 39.
A lehetőségek alkalmas csak [25, 35]. A helyes válasz - 2.
Egy másik példa a probléma megoldásának A10 vizsga számítástechnika (kérésére Eugene).
A szám vonal három szegmens:
P = [0,40], Q = [20,45], és R = [10,50].
Kiválasztása A szegmens, amely egy általános képletű ((x∈P) → (x∈Q)) ∨ ((x∉A) → (x∉R)) azonosan igaz, azaz az 1 értéket bármely értéke az x változó.
1) [5,20] 2) [10,15] 3) [15,20] 4) [35,50]
Az egyszerűség kedvéért használja a következő jelöléseket:
Most a képlet, akkor átírható az alábbi formában:
Törvény alkalmazása de Morgan, megkapjuk a következő:
A kényelem kedvéért, jelöljük az expressziós zárójelben az alábbiak szerint:
Továbbra is azt mutatják, a képlet a számegyenesen.
Úgy véljük, a kifejezés Z és mozgassa a számegyenesen
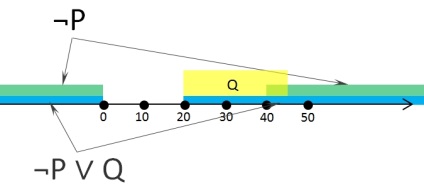
Itt van egy kijelölt zöldövezetben ¬P, sárga - Q és kék - terület ¬P ∨ Q.
Most, vegye figyelembe, hogy ez a kifejezés a zárójelben kombinált szétválás. ami azt jelenti, hogy a kapott expresszió azonosan igaz, ha legalább egy, vagy mindkét kifejezés zárójelben igazak.
Most azt látjuk, hogy ha az x változó tartozik a tartományban [-∞, 0] vagy [40; + ∞], a végső kifejezés igaz.
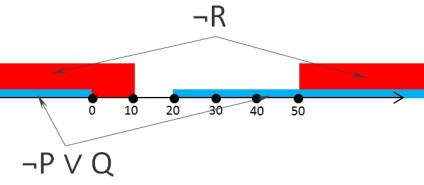
Tekintsük a második kifejezés A ∨ ¬R (I törölve az előző ábrán ¬p régió és a Q, hogy azok ne zavarják, így csak véges régió ¬P ∨ Q):
Megoldás A10 vizsga számítástechnika
Amint látható, a kifejezés a második konzol igaz lesz csak akkor, ha x tartozik a tartományban [-∞; 10] vagy [50; + ∞]. Egy általános kifejezés igaz, ha x tartozik a tartományban [-∞; 10] vagy [20; + ∞].
De ha x tartományban van (10, 20), a végső expressziós hamis. Tehát meg kell találni az érték a tartományon A, amely átfedi a szalag (10, 20). A javasolt kiviteli alak abban az állapotban kielégíti ezt a feltételt csupán a tartományban [5,20].