A divergencia a mágneses mező és a forgórész
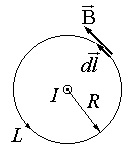
ak lásd tsirkulyatsiyaB nem függ a kör sugarát, és elhatároztam, hogy csak az aktuális vonatkozik. Megmutatható, hogy ez a tulajdonság a mágneses mező érvényes marad esetén tetszőleges formában integrációs áramkör L. és abban az esetben, ahol az átmenő területen S (cm. Ris.3.7.2) által körülzárt hurok áramok több, azaz
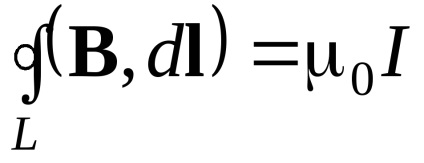

A teljes áramot jog végtelenül peremterületig ds. amelyen keresztül az infinitezimális áram dl. Egy képlet expresszáló áramot az áram sűrűsége az egész pad, azaz a Di = JDS, így a teljes jelenlegi törvény differenciális formában:
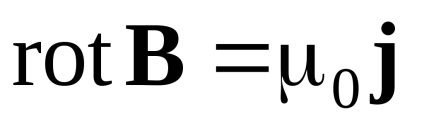

Összehasonlítjuk a differenciálegyenlet a mágneses mező a differenciál leíró egyenletek az elektrosztatikus mező (vákuumban):
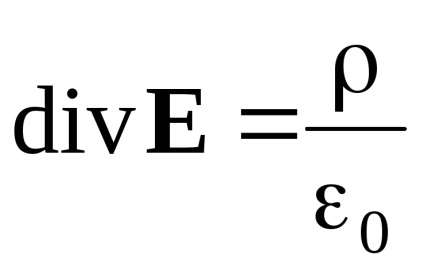
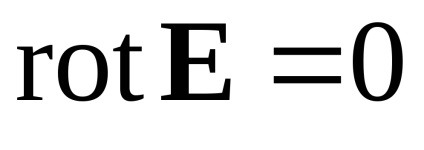
Eltérés elektrosztatikus mező nem nulla a területen forrásokból. Elektromos erővonalak kezdődik a pozitív töltések és végződhetnek negatív. A divergencia a mágneses mező mindenhol nulla. A fluxus vonalak a mágneses mező forrásától zárva van (a térerő források általában nincs értelme). A rotor az elektrosztatikus mező, mint a forgalomban, azonosan nulla. Bármely pontján az elektrosztatikus mező vektort expresszálódik a gradiens néhány skalárfüggvény úgynevezett potenciális. Az elektrosztatikus mező lehetséges. A forgórész nem nulla a területen forrásokból. Emiatt, és a forgalomban nem nulla ezen a területen. A vektor nem nem gradiens skalár koordináták függvényeként. A mágneses mező így nonpotential (vortex) ..
Így, elektromos áramot (mozgási iránya a töltés) mágneses teret hoznak létre, és
kompenzált díjak - elektrosztatikus térben. Bent a vezető van egy elektromos mező jelenléte miatt a feszültség a bemenő áram. A vezető körül van egy mágneses mező, amely megtalálható a Biot-Savart-Laplace