A problémák megoldását lineáris egyenletek
3. § A lineáris egyenletek és rendszerek
§ 24. megoldása problémák lineáris egyenletek. Az egyenlet egy matematikai modellt a probléma
Már láttunk példát a funkcionális kapcsolatok közötti értékek matematikai modellek a valós folyamatokat. Most tekintsük a szöveges feladatok matematikai modelleket, amelyek a lineáris egyenletek és egyenletek visszavezethető lineáris.
A probléma megoldásához a egyenlet alkalmazásával a következőképpen sorrendben:
1) jelöli egy változó egyik ismeretlen változók;
2) más ismeretlen mennyiségek (ha vannak ilyenek) kifejezve bevezetése változó:
3) A feltétel a probléma, hogy közötti kapcsolat létrehozása az ismeretlen és az ismert változók értékei és egyenlővé;
4), hogy megoldja a kapott egyenlet;
5) elemzése az egyenlet megoldása, és segítenek megtalálni az ismeretlen értéket, és ha szükséges, az értékek a fennmaradó ismeretlen változó;
6) írja a választ a problémára.
Vegyünk egy pár problémák és azok megoldására lineáris egyenlet.
Probléma 1. A születésnapját nővérek, ikrek Natalia és Elena összejött 127 üdvözlő SMS - üzenetek, és Natalia nyert 13 több üzenetet, mint Elena. Hány SMS-t a születésnapján minden van nővérek?
Megoldásokat. Nézzük Elena kapott üzeneteket, míg Natalie - (x + 13). És a kettő együtt - (x + x + 13) beszámol arról, hogy az állapot 127.
Jelenleg a következő egyenletet: x + x + 13 = 127. x = 57.
Tehát, Elena kapott 57 üzenet
57 + 13 = 70 (Comm.) - Natalia kapott.
A p és q az odaadó: 70 üzenetét; 57 hozzászólás.
Probléma 2. A lehetséges maximális hitel összegét számítjuk ki a bank a következő képlet szerint:
ahol S - a kölcsön összege C - az átlagos havi fizetés a hitelfelvevő. A hitel egyéves időszak tekinthető, hogy n = 9, két évig - n = 21, egy három éves időtartamra - n = 33. Mi kell a legalacsonyabb átlagos fizetés a hitelfelvevő, a bank esett neki hitelt az összeg UAH 30 000:
P a s „I H a n n i. A feltétel az S = 30 000 UAH. Hagyja a legalacsonyabb átlagos havi fizetés a hitelfelvevő UAH.
1) van az egyenlet: 30 000 = ∙ 9; ahol x = 10,000.
Következésképpen az átlagos havi fizetés a hitelfelvevő legalább 10 000 UAH.
2) Van az egyenletet: 30 000 = ∙ 21; ahol x ≈ 4285,7.
Következésképpen az átlagos havi fizetés nem lehet kevesebb, mint 4286 USD.
3) van az egyenlet: 30 000 = ∙ 33; ahol x ≈ 2727,3.
Tehát, ha a hitelfelvevő akar kölcsön három évig, az átlagos havi fizetés nem lehet kevesebb, mint 2728 USD.
A p és q az odaadó: 1) 10 000 USD; 2) 4286 USD; 3) 2728 UAH.
Probléma 3 Városról városra A B. amelyek közötti távolság 310 km, balra teherautó. 30 perc múlva, akkor B-től Város A balra személyautó, amelynek sebessége 20 km / h-nál nagyobb a sebesség a rakomány. Gépkocsik találkozni 2 óra után elhagyja az autót. Keresse meg a sebességet az egyes járművek.
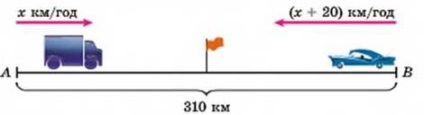
P a s „I H a n n i. Hagyja, hogy a sebesség a teherautó - x km / h. Feltétel Probléma kényelmesen bemutatott egy táblázatot:
Mivel az autó hajtott ellentétes irányban teljesül, akkor együtt utaztak 310 km.
Megvan az egyenlet: 2 5x + 2 (x + 20) = 310.
Megoldani: + 2,5 x 2 + 40 = 310; 4,5 = 270;
X = 60 (km / h) - egy tehergépjármű sebessége;
60 + 20 - 80-ig (km / h) - személygépkocsi sebesség.
Válasz: 60 km / h; 80 km / h.
Milyen sorrendben kell követni, a probléma megoldásának segítségével az egyenlet?
892. (orálisan) slotszám 20 nagyobb, mint a második. Kevesebben x jelöl. Expressz révén x több ilyen számokat.
893. (orális) Egy pozitív szám 5-ször nagyobb a második. Kevesebben x jelöl. Expressz révén x több ilyen számokat.
894. Az ember virágágyásba termesztés rózsabokrok, és a második - kétszer annyi. Express x összeget rózsabokrok, hogy a nő a második virágágyásba.
895. (orálisan) egyenlő távolság x km kerékpáros legyőzi 5 órán át. Expressz x keresztül mozgási sebességét.
896. (orálisan) Az első szám jelöli x, és a második egy negyede a korábbi. Fejezzük ki a második számot x.
897. Az első szám egyenlő x. és a második 70% -a az első. Expressz x keresztül a második számot.
898. (orálisan) teljes hosszának a két vonal szegmensek 10 cm. A hossza egy más cm. X Express révén a hossza a második szegmens.
899. (orálisan) En hajó sebessége 18 km / h, és az áramlási sebesség - x km / h. Kifejezve x motorcsónak downstream és upstream.
900 ismeretlen szám. Ha az előírtnál 7. és ossza meg az eredményt 9 vele, megkapjuk 12. Hány teszik valóra?
901. Keresse meg a számot, amelynek a fele, együtt harmadik rész 40.
902. A két tartály 58 tonna üzemanyag, valamint az első, t4 értéke kisebb, mint a második. Hány tonna üzemanyagot minden egyes tartály?
903. A flotta teherautók 6-szor nagyobb, mint az utas. Hány autót a parkolóban, ha a rakomány 91?
904. Az egyik két pozitív egész szám háromszor nagyobb, mint a második. Ezeket a számokat, ha a különbség eléri a 28.
905. Nagymama édesanyja 99 éves. Hány éves mindegyikük, ha a nagymama idősebb anya 25 éve?
906. A összege két szám 360 és arányuk egyenlő 5 7. Keresse meg a számot.
907. A különbség a két szám 42 és azok aránya egyenlő 7. 4. megtalálni a számot.
908. A kerülete a háromszög egyenlő 20 dm. Két oldala egyenlő, és ezek mindegyike 1 dm nagyobb, mint a harmadik. Keresse meg a háromszög oldalainak.
909. Két nap volt, 384 kg értékesített banán, ahol a második napon eladott, hogy értékesítik először. Hány kilogramm banánt értékesítik az első nap, és mennyit - a második?
910 turisták a második napon eltört által megtett távolságot az első napon. Hány kilométert legyőztem az első turisták a nap, és mennyi a második, amikor fogott el 3 km többet az első napon, mint a második?
911. A mosógép és a kapcsolat fizetett 2940 USD. Csatlakozási díj 5% -a költsége a gép. Mennyibe kerül a mosógép?
912. nagyi öntött gombócokat két órán keresztül. A második órában, ő öntött egy 5% -kal több, mint az első gombóc. Hogyan gombócokat készített egy nagymama az első órában, és a második, ha a második óra múlva vágású 3 gombóc több, mint az első?
913. 2 órán motoros legyőzi azonos távolságra, mint a kerékpáros 5 órán át. A sebesség a motoros 27 km / h feletti sebesség a kerékpáros. Keresse meg a sebességet mindegyikre.
914 fiók a narancs 3 kg nehezebb, mint egy doboz citrom. Mi a súlya mindegyikük, ha a tömeg a négy doboz narancs megegyezik a tömege öt doboz citrom?
915. Városról turisztikai település séta sebességgel 4 km / h, és jött vissza a sebesség 3 km / h. Egész úton töltött 7 óra. Keresse meg a távolság a város szélén.
916. A kerülete a téglalap egyenlő 36 cm-es, egyik oldalán 4 cm-rel nagyobb, mint a másik. Keresse az oldalán a téglalap és környékén.
918. Masha háromszor több pénzt, mint Oli. Miután Mary töltött 18 UAH, a pénz a lányok egyenlő volt. Mennyi pénzt kellett minden a lányok újra?
919. A hálózat édesipari évfordulójára nyitás adta a látogatók egy sor védjegyek édesség „Jó”, „édes” és „finom”. A végén az ünneplés kiderült, hogy a készlet „édes” kapott 12 több, mint egy sor „jó”, és a készletek „Delicious” - több mint 31 &всехuo;Édes. " Hány szett minden márka adtunk, ha a látogató volt 430 és mindegyik kapott egy készlet?
920. Az egyik oldalon a háromszög 9 cm, és kisebb, mint a második fele a harmadik. Keresse meg a háromszög oldalainak, ha a kerülete 105 cm.
921. Meg lehet bővíteni 68 konzerveket a három doboz, hogy a második kétszer több doboz, mint az első, és a harmadik - a 3 bank kisebb, mint az első?
922. Azt is megteheti, tegye a 90 könyv három polcokat is, hogy a harmadik pedig a 3 könyv több mint egy második, és 5 könyvet kevesebb, mint az első?
923 Apa most - 38 éves, és fia - 10. Miután hány évig lesz az apa háromszor idősebb fiát?
924 Egy részét egres bokrok és háromszor nagyobb, mint a második. Ha az első graft 12 rész a második bokrok, a bokrok egres mindkét helyen lenne egyenlő. Az, hogy mennyi egres bokrok nőnek minden területen?
925. A két esetben azonos számú bentlakásos élt tartózkodást. A kapcsolat a javítás, úgy döntöttek, hogy helyezze át a nyugalmi 24 első ház a második, majd a vendégek száma az első esetben volt 4-szer alacsonyabb, mint a második. Sokak szerint a turisták tartózkodtak minden esetben megkezdése előtt javítási munka?
926. A két zsák cukor egyformán. Miután az első öntsünk zsák 8 kg a második, ez volt kétszer kevesebb cukrot, mint a második. Az, hogy hány kilogramm cukor volt minden zsák először?
927. A 33 hrivnya 24 notebook vásárolt vonal és a sejt. Notebook ár soronként - 1 UAH 20 kopeks. és a doboz - 1 UAH 50 kopeks. Az, hogy mennyi minden típusú vásárolt notebook?
929. ógörög feladat. Püthagorasz megkérdezték: „Hány diák tanul az iskolában?”. Erre ő azt felelte: „fele az én tanuló diákok matematika, a negyed - a zene, a hetedik rész csendes, és ezen túlmenően van három nő.” Hány diák iratkozott be az iskolába Pitagorasz?
930. Súly doboz tejjel 25 kg, és a felét a súlyát. Mi a súlya egy doboz tejet?
931. egy szám egyenlő - a második. Ezeket a számokat, ha az összegük 66.
932. 60% számos egyenlő 45% az utóbbi. Ezeket a számokat, ha az összegük egyenlő 210.
933. A hajó töltött patak útját 2,5 óra és 3,6 óra upstream. A távolság, amelyet a hajó úszott a folyón lefelé, kiderült, hogy a 7.6 km-nél kisebb a távolság, ami úszott az árral szemben. Találd meg a saját motorcsónakkal, ha az áramlási sebesség értéke 2 km / h.
934. A hajó vitorlázott a folyó mentén 1,6 óra, és upstream - 2,5 óra. Által megtett hajóval szemben a jelenlegi, volt na 6,2 km több, mint a távolság, amelyet a hajó sodródik. Találja meg az áramlási sebesség, ha a motorcsónakos 16 km / h.
935. pontból a B pont a sebesség 12 km / h hajtott a kerékpáros. 3 óra múlva a B pont bekezdésben egy motoros balra sebessége 45 km / h. Hány órát az ülés előtt egy motoros lovaglás kerékpáros, ha a távolság az A B 235,5 kilométert? Hogy milyen távolság a pont volt az ülés?
936. A vendégház felé vasútállomáson sebességgel 14 km / h hajtott a kerékpáros, és 2 óra múlva az azonos, de az ellenkező irányba sebességgel 4 km / h ment gyalogos. Miután több órát a megjelenése után lesz egy gyalogos a parttól 73 km-re a kerékpáros? Milyen messze ezúttal a ház, ő lesz?
937. egy görögdinnye 5 kg-mal könnyebb második és háromszor könnyebb, mint a harmadik. Az első és a harmadik a görögdinnye együtt kétszer nehezebb, mint a második. Keresse meg a tömeg az egyes görögdinnye.
938. A felkészülés a Diákolimpia matematika Ivan döntött 3 feladatok kisebb Oksana, és 2-szer kisebb, mint Szergej. Ugyanakkor, Ivan és Sergey együtt elszabadult 2,1-szer több problémát, mint Oksana. Mi a feladatok száma döntött minden tanuló a felkészülés az olimpiára?
Gyakorlatok megismételni
5. A 3. egyenlet vagy azzal egyenértékű - 2 = x + 8 + 2 (x - 3) = x - 1?
6. Egy kosár két szer több gombák, mint a második. Hány gombák minden kosár, ha a két kosarat együtt 78 gombát?
2) 5X - (x + 5) = 4 (x - 2).
8. Hajó downstream lebegett 3,5 órán át, és upstream - 4,2 óra. A távolság, amelyet a hajó úszott a folyón lefelé, kiderült, hogy 9,8 km-rel hosszabb, mint a távolság, amely úszott az árral szemben. Találd meg a saját motorcsónakkal, ha az áramlási sebesség értéke 2 km / h.
9. összes integer értékeit, amelyek gyökere az egyenlet ax = -6 egész szám.
10. Oldja meg az egyenletet | 3-4 | = 5.
11. A város a falu elment egy gyalogos sebességgel 4 km / óra. 2 óra elteltével a vidéki városi kerékpáros utazott sebességgel 16 km / h. Hány órát az ülés előtt egy gyalogos kerékpáros lovaglás, ha a távolság a falu a város 38 km-re?