Vektor és skalár komponensei a vektor, a döntés Mathematic feladatok
Ábra. 3.22. Vektor vetülete a vektor a gépen.
Ábra. 3.23. Vektor vetülete a tengelyen.
A vektor algebra gyakran szükséges, hogy tervezzen egy vektor egy tengely mentén, amely egy egyenes vonal, amelynek előre meghatározott orientációban. Az ilyen tervezése könnyen elvégezhető, ha a vektor az L, és a tengely egy síkban fekszik (ábra. 3.23). Azonban a feladat bonyolultabbá válik, ha ez a feltétel nem teljesül. Készítünk vektor vetülete a tengelyen, a vektor és a tengely egy síkban fekszik (ábra. 3.24).
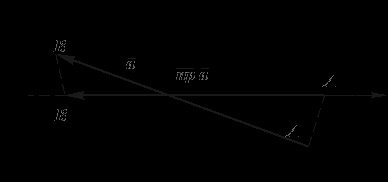
Ábra. 3.24. Tervezés vektor a tengelyen
az általános esetben.
Bizonyítsuk be, hogy a párhuzamos átvitel vektorok vektor vetülete nem változik.
Miután tartja a végeit a vektor sík, L. A merőleges keresztezi az egyenes vonal a sík adatok határozzák meg két pontot az A1 és B1 - vektor, amelyet az úgynevezett vektor vetületét a vektor. A probléma, hogy találnak egy vektor vetülete lehet megoldani könnyebb, ha a vektor látható egy síkban a tengellyel, lehetséges, hogy végre, hiszen a vektor algebra mentesnek tekinthető vektorok.
Együtt a vetítési vektorral, van egy skalár vetítés, amely egyenlő a vektor vetítőkészülék, ha a nyúlvány egybeesik a vektor tájolótengelyt L, és egyenlő nagyságú, vele szemben, ha a vektor vetítési tengelyen L és az ellenkező orientációban. Skaláris vetítés jelöljük:
Vektor és skalár vetítés terminológia nem mindig szigorúan elkülönítve a gyakorlatban. Általában használja a „vetülete”, utalva arra, hogy a skalár vetülete a vektor. A feladatok megoldásában világosan meg kell különböztetni ezeket a fogalmakat. Miután a hagyománya, használjuk a „vetülete”, azaz skalár vetítés, és a „vektor vetítés” - összhangban megállapított jelentését.
Belátjuk a tétel lehetővé teszi, hogy kiszámítja a skalár vetülete egy adott vektor.
5. Tétel A vetítés vektort a tengelyen L egyenlő a termék a maga a modul a koszinusz közötti szög a vektor és a tengely, azaz
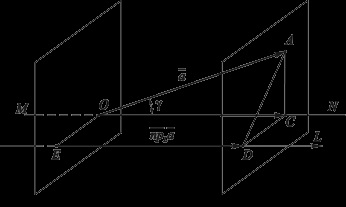
Ábra. 3.25. Megtaláljuk a vektor és skalár
Projection vektor ra tengelyre L
(És L azonos tájolási tengely).
Bizonyítás. Végezze pre-építés, amely lehetővé teszi, hogy az a szög, a vektor és a G tengelye L. E konstrukció vonal MN, L, a tengellyel párhuzamos, és áthalad az O pont - start vektort (3.25 ábra.). A szög a kívánt szöget. Keresztül a pont, A és D a két sík, L. merőleges tengely kapjuk:
Mivel a tengely az L és a vonal MN párhuzamos.
Két esetet különböztetünk kölcsönös helyvektora és a tengely L.
1. Legyen a vektor vetítési tengelyen L és azonos orientációban (ábra. 3,25). Ezután a megfelelő skaláris vetítés.
2. Legyen L, és úgy orientáltak ellentétes irányban (ábra. 3,26).
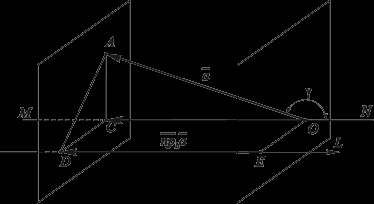
Ábra. 3.26. Megtalálása vektort és egy skalár a vektor kiemelkedések tengelyen L (tengely L és orientált ellentétes irányban).
.
Így mindkét esetben az az állítás, a tétel.
Tétel 6. Ha az eredete a vektor kap egy pontot a tengely L, és ez a tengely található, a s síkban képez vektort vektorral s a gépen a vetítési szög, és a vektorral vetülete a tengelyen L - szög továbbá magukat vektor nyúlványok szöget zárnak majd
Bizonyítás. Háromszögek OAB, OBC és az SLA - téglalap alakú, így
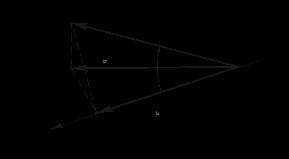
Ábra. 3.27. A vektort és a vektort vetülete a síkra S és L tengely síkjában fekvő
(A tengely L és ugyanolyan orientációban).
Állami és bizonyítani a tételt, amikor nem minden szögből A. B Mindig éles (ábra 3.28).
A fenti tétel fontos, nem csak a vektor algebra, de lényeges megoldásában sok problémát stereometrical.
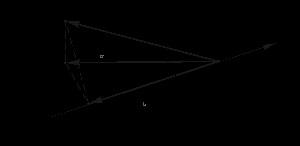
Ábra. 3.28. Vektor és vektorhoz vetítési
Az S sík és az L tengely síkjában fekvő
(L tengely és ellentétes orientált).