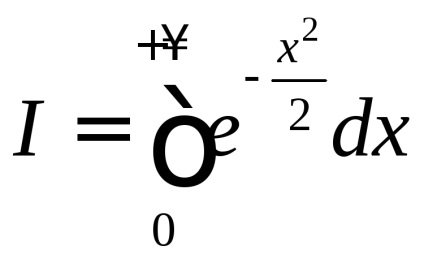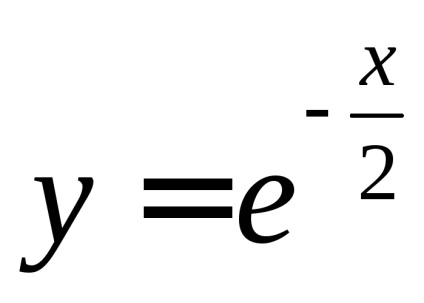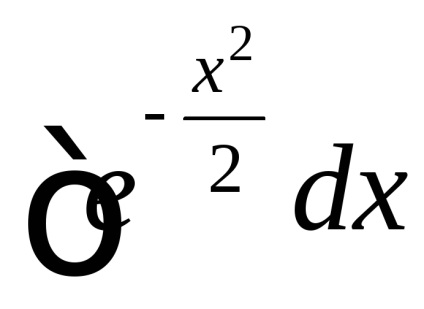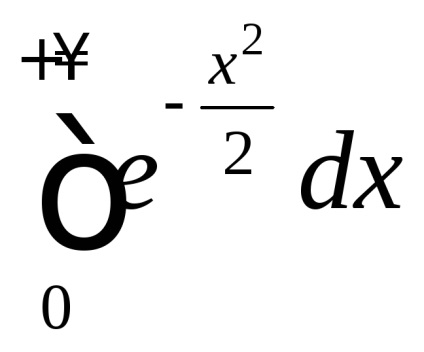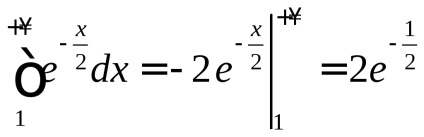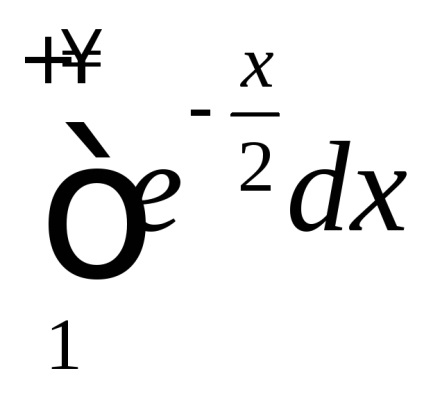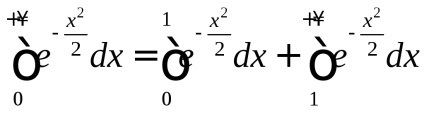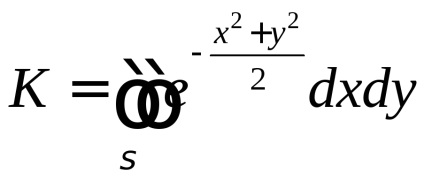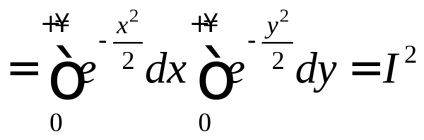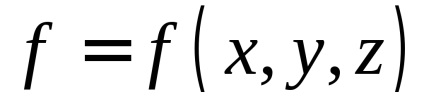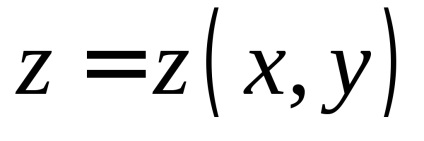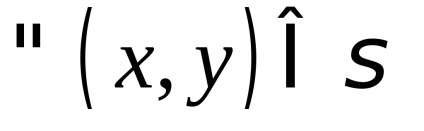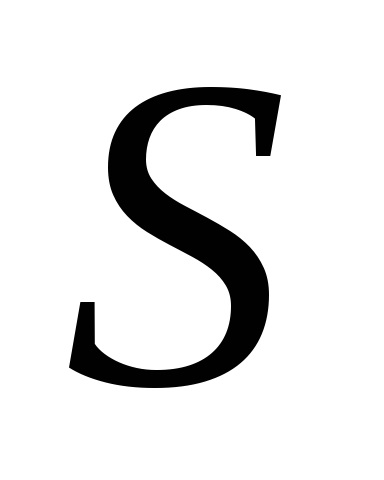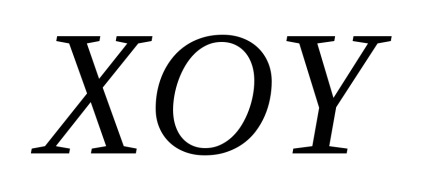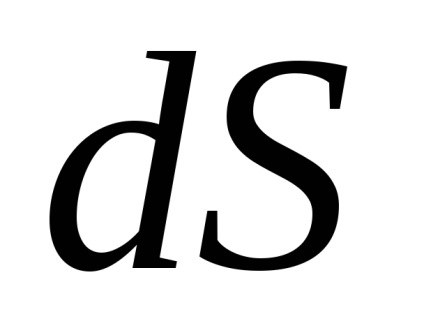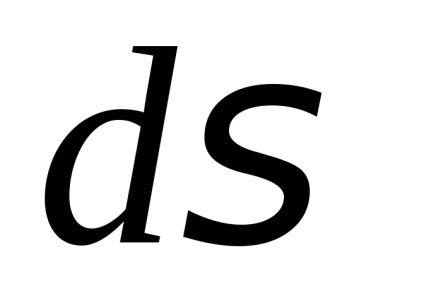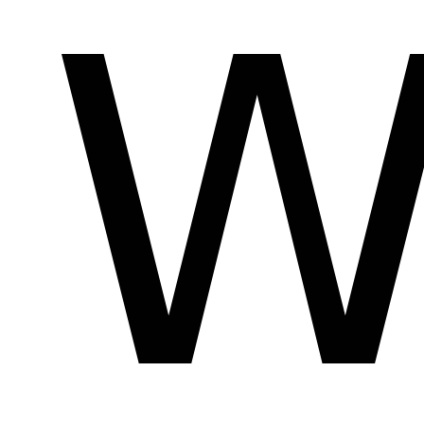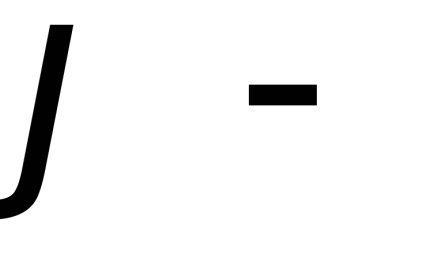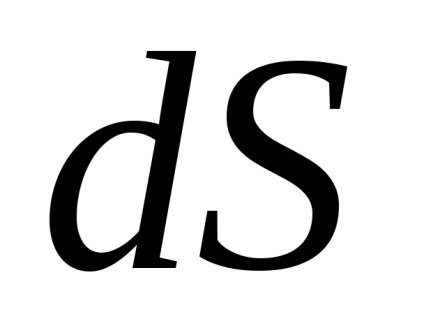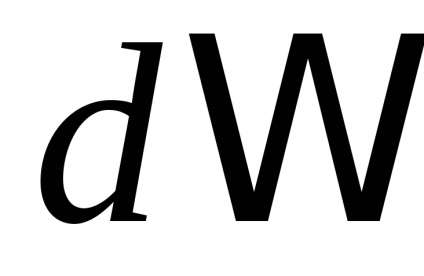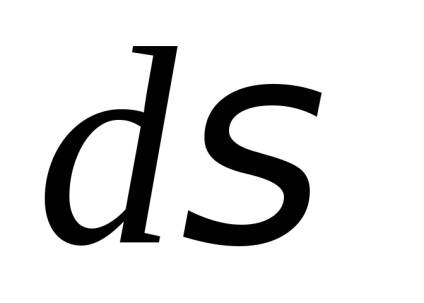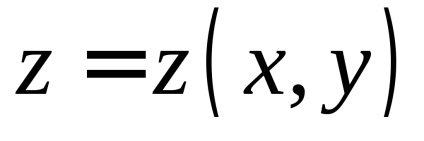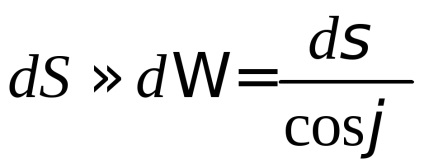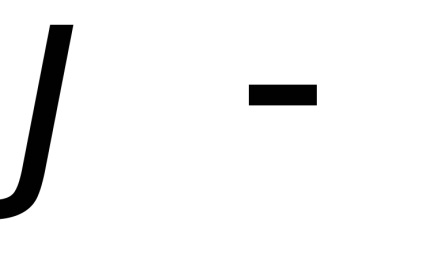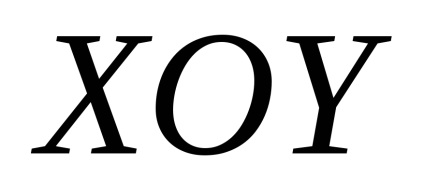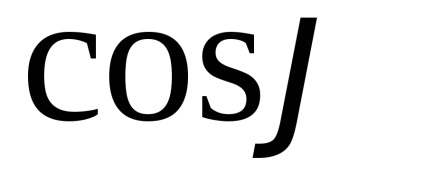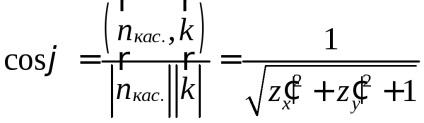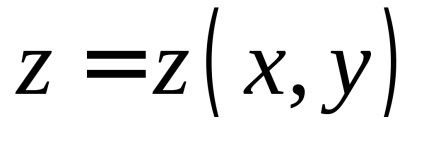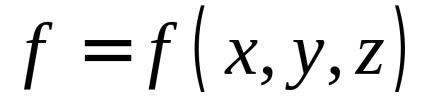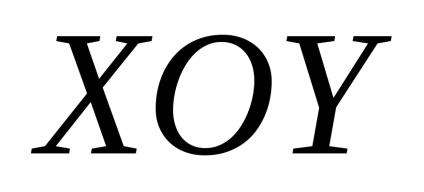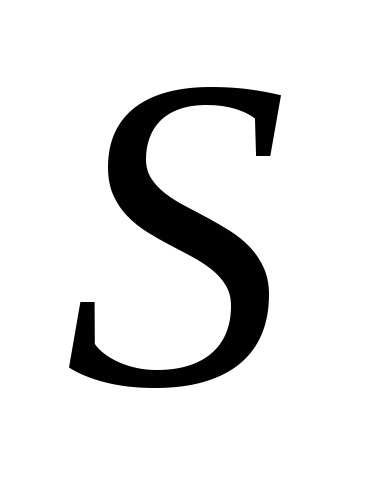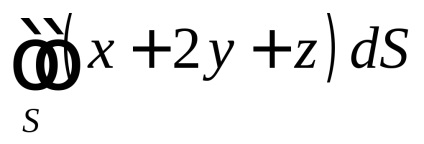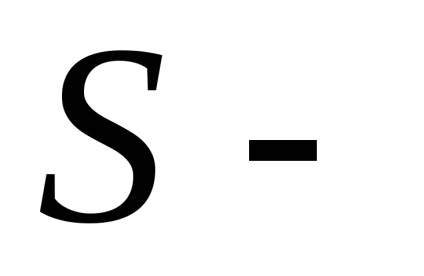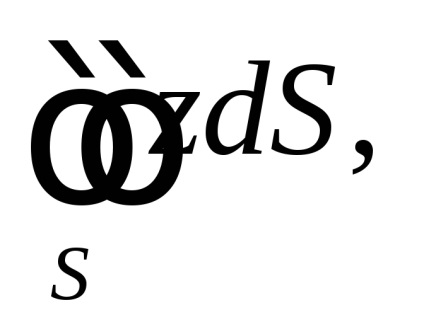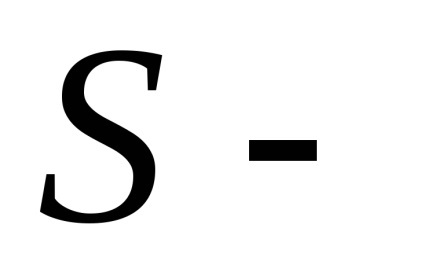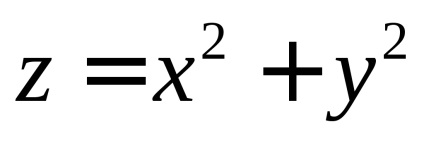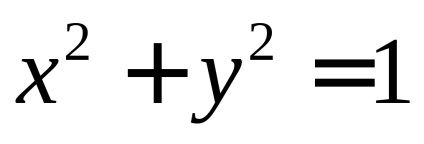Poisson szerves

A valószínűségszámítás fontos szerepet játszik a megfelelő szerves

, amely az úgynevezett Poisson integrál. Amint azt a 7. fejezet, a függvényEz nem elemi primitív és a határozatlan integrálArra utal, hogy az úgynevezett „neberuschimsya” integrál. Ahhoz azonban, hogy kiszámítja a helytelenlehetséges. Megtalálása előtt érték, ellenőrizze, hogy konvergál.

Mivel akkor, de

, azaz definíció szerint a konvergencia nem megfelelő integralovI fajtája konvergál. ezértkonvergál alapján az összehasonlítást.

Értékének kiszámításához a Poisson szerves alkalmazni ezt a megoldást: Tekintsük a kettős integrál

, ahol a domain az integráció az első negyedévben a koordinátasíknak (ris.56).

Derékszögű koordináta

(Emlékezzünk, hogy az érték a határozott integrál független a szimbólum a változó integrációs).

Másrészt, átadva polár koordinátákkal, kapjuk:

.

8.13. A számítás a felületi integrál az első fajta (felületi területe)

Let felület

, egyenlet által definiált, folytonos függvény van definiálva. A meghatározás szerint a felületi integrál az első fajta ezt a funkciót nevezik

,

ahol a pontokat, és

- egy kis része a felszín, amelyben van osztva a készítmény egy integrált mennyiségű (10. ábra).

Feltételezzük, hogy a funkció

differenciálható, azaz minden tochkeS levonhatjuk érintő sík.

vidék

nyúlványa gépen. Express sejtfelszínikeresztül vetítés(Fig.57). Ehhez használjuk a jól ismert: if - vetülete egy sík régió, amelynek területe, az, aholA síkja közötti szög régiót és a vetítési sík.

Döntetlen egy tetszőleges helyen kiválasztott felületi elem

érintősík, és hagyja, hogy- azt a részét, amely az előrejelzések rá a. Mivel a függvénydifferenciálható, az elem nagysága, aholközötti szög az érintő sík és, amely egyenlő a szög közötti merőlegesek.

kiszámítjuk

. Ha átírjuk felület egyenletehallgatólagosan, majd (lásd. 6. fej.) apoetomu(Lásd. Fejezet. 2.).

A pontokat a felület

, ahol, függvény veszi az értékek azonban összhangban a meghatározása a felületi integrál az első fajta lehet csökkenteni a kettős integrál:

Így, a számítás a felületi integrál az első fajta csökken egy számítást a kettős integrált a vetítési felület síkban

.

Megjegyzés. Ha a felület

amely az előrejelzések szerint egy másik koordinátarendszerben, az (8.17) és (8.18) megfelelően fog változni.

P

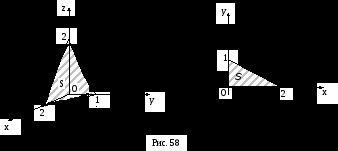
Rimer. számol , harésze sík, található az első oktáns (ris.58).

Az egyenletből megkapjuk a sík:

. Továbbá, minden pont a síkon az ingatlan poetomu- 1 határozott integrál: a vetítési területen

(Ris.58) nyilván értéke 1.

Tekintsünk egy kicsit bonyolultabb példát.

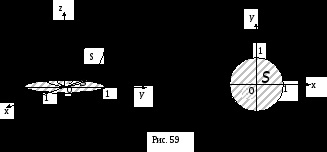
Példa. számol

haelliptikus paraboloid felületrész, ez kivágtuk a henger(Fig.59).

Kapcsolódó cikkek

• Több integrálok, 3. oldal