Előadás a központi kiemelkedés, valamint párhuzamos és merőleges

Előadás témája: „Együtt az alappálya párhuzamos és merőleges vetülete, használt a geometria a kép térbeli alakzatok, nagyon.” - átirata:

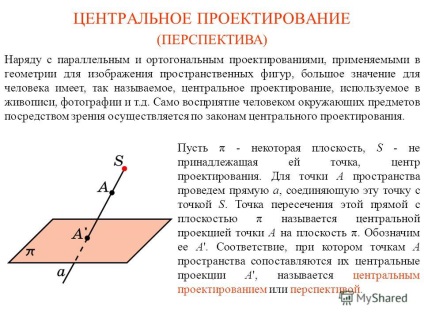
1 a központi nyúlvány együtt párhuzamos és merőleges előrejelzések, használt a geometria a kép térbeli alakzatok, nagyon fontos, hogy az ember az úgynevezett központi kiemelkedés használt festmények, fényképek, stb A nagyon észlelése személy útján környező tárgyak által hordozott törvényei előrejelzésben. Let π - egy sík, S - nem tartozik az ő pont, a design központjában. Egy pont tér húzzon egy vonalat a, az összekötő pont a lényeg S. metszéspontja E síkjával párhuzamosan π nevezzük vetülete a központi pont a síkon π. Jelölje az A”. Value mely pontokon A tér, mint az alappálya A”, az úgynevezett perspektíva vagy a központi vetítés. (Outlook)

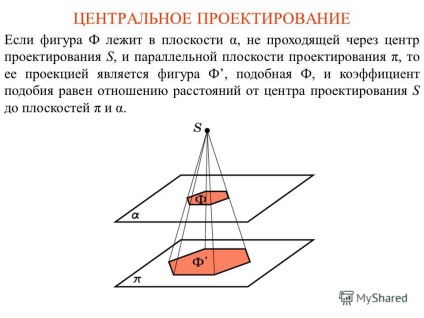
2 központi kiemelkedés Ha a szám F síkjában fekszik α, amely nem halad át az S design központ, és párhuzamos a vetítés síkra π, akkor a vetítés az ábrán F, a F, és a hasonlóság arány az arány a távolságok a nyúlvány központ S a síkok π és α.

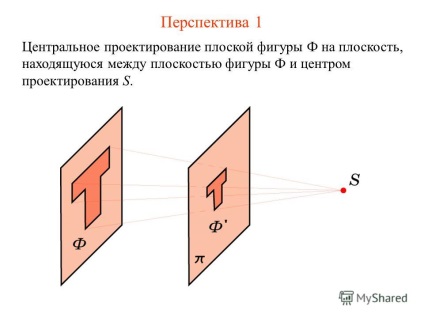
3 Perspective 1 központi kiemelkedés síkidom F egy síkban helyezkedik között az ábra síkjából F és tervezési központot S.

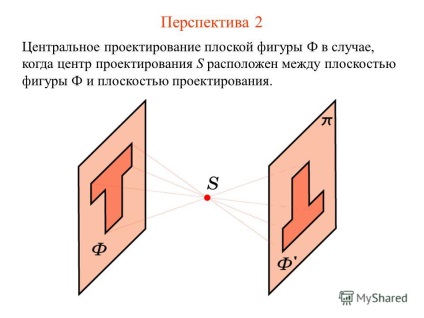
4 Perspective 2 központi kiemelkedés síkidom F abban az esetben, ahol S design központ között található az ábra síkjából F és vetítési sík.

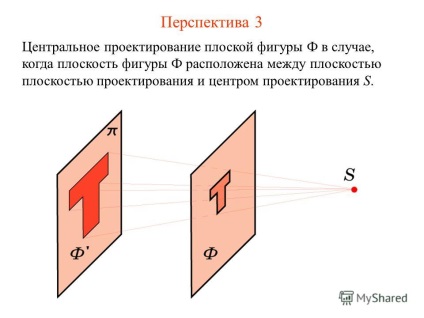
5 Perspective 3 központi kiemelkedés síkidom F abban az esetben, ha a sík alakú F között található a síkban tervezés és design központ S.

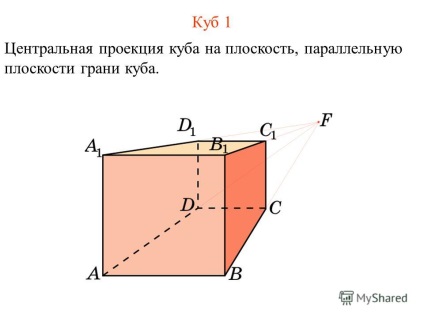
6 Cubic 1 elõrejelzés kocka síkra síkjával párhuzamos arcok a kocka.

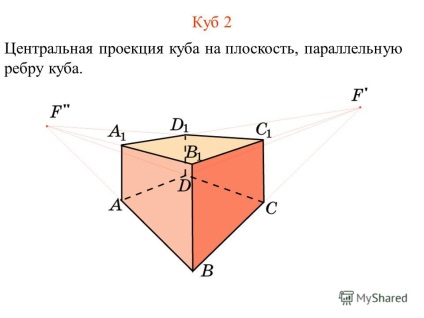
7 Cubic 2 Közép vetülete kocka-ra egy párhuzamos síkban egy kocka éle.

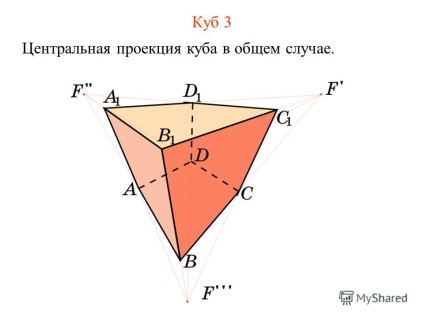
8 Cubic 3 központi vetülete a kocka az általános esetben.

4 9 köbös központi kiemelkedés a kocka az általános esetben.

Központi vetítés 10 Piramis rendszeres négyszögletes piramis.

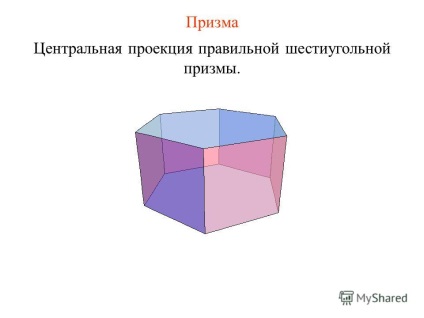
Központi 11 nyúlvány Prism szabályos hatszög hasáb.

A központi nyúlvány 12 a henger hordó.

13 A. A gravírozás Durer Durer (1471-1528) előállítását mutatja perspektivikus képe az objektumot a kifeszített izzószál.

14 N. N orosz művész és tanár NN N (1834 - 1894), utalva az ő tanítványai, mondván: „Tanítsd a jövőben, és amikor ti bírják azt, hogy azt a munkát, a rajzban. Itt bemutatunk egy képet NN N „I. Péter lekérdezi Tsarevich Alexei”

15 IE Repin () Váratlan

17 1. gyakorlat az összes hely van a központi vetülete pontokat? Amely rámutat, hogy nem is létezik? Válasz: Nem Nem létezik a pont a síkon közepén keresztül a tervezés és a párhuzamos tervezése a gépet.

18 2. gyakorlat Can alatt alappálya párhuzamos vonalak metszik go? Válasz: Igen.

19 3. gyakorlat Ebben az esetben, a központi vetülete a két egyenes két párhuzamos vonal? Válasz: Ha a vonalak párhuzamosak a vetítési sík.

20 4. gyakorlat Mi a kép a kapott érték a központi kiemelkedés, ha a vetítési sík között helyezkedik el az ábrát és a design center? Válasz: Csökkentett közvetlen.

21 5. gyakorlat Mi a kép a kapott érték a központi kiemelkedés, ha a design center között helyezkedik el ez a szám és a design a gépet? A reverz.

22 6. gyakorlat Mi a kép a kapott érték a központi kiemelkedés, ha található síkja közötti tervezési és tervezési központot? A: A növekedés a közvetlen.

23 7. feladat Mi a helyzet a központi vetülete egy síkidom, amelynek székhelye a párhuzamos síkban a sík a design? Válasz: Ez lesz az eredetihez hasonló.

24 8. gyakorlat Legyen az egyenes vonal metszi a sík és átmegy a ponton S. Point, a rajz, ahol a központi kiemelkedés belép egy egyenes szakasza, található: a) „a fenti”; b) „alatt” a gépet. Válasz: a) Ami AD és SC-sugarak elvek nélkül, azaz pont nélkül és az S; b) szempontjából a szegmens nélkül a végei, azaz a pontok nélkül az A és S.

Exercise 25 9. ábra a központi kiemelkedés a kocka. Magyarázza minden esetben egy kocka síkjához képest a vetítés. Válasz: a) Él ADD 1 1 kocka síkjával párhuzamos vetítés; b) a szélén a kocka párhuzamos egy BB vetítési síkban; c) az arc ABCD kocka párhuzamos vetítés sík F és fekszik a képen az arc; d) vetítési sík nem párhuzamos semmilyen szélén a kocka.

Exercise 26 A 10. ábrán egy központi kiemelkedés megfelelő négyszögletes gúla. Magyarázza meg, hogyan van pozícionálva a vetítési sík. Válasz: a) párhuzamos síkban a piramis alapsíkkal kialakítás, valamint a közvetlen SM merőleges vetülete síkban ahol S - a design központ, M - a csúcsa a piramis; b) egy bázis, síkja a piramis párhuzamos a vetítés síkra; c) egy alaplap nem párhuzamos síkja vetítés.

Exercise 27 A 11. ábra a központi vetülete egy jobbmenetes henger. Mivel a henger van elhelyezve síkjához képest a tervezési? Válasz: A párhuzamos síkban bázisok a henger design.

Exercise 28 12 Doris központi kiemelkedés kocka ABCDA 1 B 1 C 1 D 1 egy síkban síkjával párhuzamos az arc ABB A A 1. 1.

Gyakorlat 29 13 távolság a központtól a vetítési felület síkja 1 A 1 ABB kocka ABCDA 1 B 1 C 1 D 1 az ábrán látható: 10. Keresse meg a távolság a központtól síkján up design CDD C 1 1. Válasz. 20.

Exercise 30 14 Doris központi kiemelkedés kocka ABCDA 1 B 1 C 1 D 1 egy síkban síkjával párhuzamos az arc ABB A A 1. 1.

Exercise 31 15 távolság a központtól a vetítési felület síkja 1 CDD kockát ABCDA C 1 1 B 1 C 1 D 1 az ábrán látható a 16 Find a szélén a kocka. Válasz. 8.

Exercise 32 16 Draw központi kiemelkedés kocka ABCDA 1 B 1 C 1 D 1 merőleges síkban, hogy a szélén AA 1, S design központ fekszik a kiterjesztése a bordák. Válasz.

Exercise 33 17 Draw központi kiemelkedés kocka ABCDA 1 B 1 C 1 D 1 egy síkban nem merőleges a szélén AA 1, S design központ fekszik a kiterjesztése a bordák. Válasz.

Exercise 34 18 Draw központi kiemelkedés kocka ABCDA 1 B 1 C 1 D 1 a merőleges síkban az AC átló 1, S design központ fekszik a kiterjesztése az átlós. Válasz. A számok azt mutatják, a kapott képek számítógépes programokat.

Exercise 35 19 Single köbös ABCDA 1 B 1 C 1 D 1 vetíti sík felületeivel ABB 1. A 1. Az oldalán a tér, amely kiemelkedés arcok CDD 1 C 1 egyenlő 0,4. Keresse meg a távolság a központtól a tervezéstől a design a gépet. Válasz.

Gyakorlat 36 20 Döntetlen alappálya rendszeres négyszögletes piramis SABCD merőleges síkban a szélén AS, S design központ fekszik kiterjesztése a bordák. Válasz.

Exercise 37 21 Draw központi vetülete egy szabályos hatszög hasáb ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 merőleges síkban a szegmens OO 1 középpontjával összekötő -a, a vetítési centrummal S fekszik a folytatása ebben a szegmensben. Válasz.

Exercise 38 22 szabályos hatszög hasáb ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, az összes a széleit, amelyek 1, vetíti a felület síkja A 1 B 1 C 1 D 1 E 1 F 1. Az oldalán a hatszög, amely kiemelkedés arcok ABCDEF egyenlő 0,6. Keresse meg a távolság a központtól a tervezéstől a design a gépet. Válasz. 1.5.

Exercise 39 23 Draw központi vetülete egy szabályos hatszög hasáb ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 merőleges síkban, hogy a szélén AA 1, S design központ fekszik a kiterjesztése a bordák. Válasz.

Exercise 40 24 Draw központi vetülete egy szabályos hatszög hasáb ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 merőleges síkban a szegmens középpontját összekötő szemközti oldallal, S design központ fekszik a folytatása ebben a szegmensben. Válasz.

Exercise 41 25 Draw központi vetülete egy szabályos hatszög hasáb ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 merőleges síkban a összekötő szakasz felezőpontja átellenes oldalsó szélei, a középső S tervezési fekszik a folytatása ebben a szegmensben. Válasz.