Jelenlegi fémekben
Nature elektromos áram hordozókkal fémek hozta létre az alábbi kísérletekben.
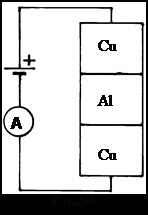
a. Kísérletek Richard Tolman munkatársai (T.Styuard). 1916-1926 g kidolgozott elképzelések Mendelshtamma Papaleksi, és feltéve, hogy az első kvantitatív eredményeket.
A tekercs nagy számú fordulattal sodorva saját tengelye körül, majd hirtelen fékezni. A végén a tekercs huzalok lehet csavart és már csatolt egy ballisztikus galvanométer. A mágneses mező a föld gondosan kompenzált vezeték. Fékezéskor tekercs galvanometer adta szemetet.
Ha m - lendkerékkel elektromos töltéshordozók, és e töltésük, a változás a fékező impulzus töltéshordozók egyenlő (mN) dv = Fdt = (EN) Edt (9.1)
Ahol n a száma töltéshordozók a nagy részét a tekercs huzal.
Elosztottuk az N, valamint figyelembe véve, hogy az E = Uçl. ahol U - a feszültséget a végén a drót, és l - a hossza, és hogy az U = Ri; ahol R - az áramkör ellenállása, és én - az áram az áramkörben, megkapjuk a változás az impulzus töltést hordozó egységet.
Integrálása a lefutási idő a tekercs, megkapjuk:
Lineáris forgási sebesség v = 300 m / s, a tekercs vezeték hossza L = 500 m. Kísérletek réz, alumínium, ezüst huzalok. Amikor különböző áramköri ellenállások R és értékeit különböző mért galvanométer fajlagos töltés q töltéshordozók fordult egyenlő és azonos az eçm = 1,6 × 11 okt C / kg. Ez volt közel a kapott eredmények J. Thomson húsz évvel korábban kísérleteket katódsugarakkal.
Az eredmények összefoglalása ezeknek a válaszoknak eredményeként az alábbi következtetéseket:
Carriers elektromos töltések minden fémek jelentése azonos;
Elektromos töltéshordozók fémek elég anyag, van tehetetlenség és lazán kötődik a fém rács.:
A konkrét töltéshordozók eçm = 1,6 × 11 okt C / kg.
Mivel ebben az időben (a végén a 20-as évek XX század) Millikan határoztuk elemi töltés e = 1,6 × 10 -19 Cl, akkor lehetett becsülni a tömege inert hordozókkal. .
Töltéshordozók fémek megjelent elektronok észlelt korábban a katód sugarak (1897) és a termoelektromos felhő fém-nátriumot. (1988, T. Edison).
Általában az elektromos vezetőképesség kell tekinteni, mint a jelenség az anyag továbbítása és az elektromos töltés. Jogszabályai szerint az utóbbi esetben az Ohm-törvény.
2.Electronic elmélete vezetőképessége fémek. Az első évtizedben a XX században, Paul Drude és Hendrik Lorentz épült klasszikus, azaz Maxwell egyenlet alapján az elmélet elektronvezetőképességgel fémek.
Azt állították, hogy a vegyérték elektronok a fémek kötött atomjaik olyan gyenge, hogy könnyen mozog az egyik atom egy másik csak annak az energiának a termikus mozgás. Az ilyen készlet a vegyérték elektronok értelmezték őket egy elektron gáz engedelmeskedik a Maxwell-Boltzmann statikus és amely olyan tulajdonságokkal ideális.
Idealitás elektrongáz azt jelenti, hogy a vezetési elektronok nem ütköznek egymással, ezek ütköznek egy rácsos csomópontok velük, és a termikus egyensúlyban. Ez a feltétel, meg tudjuk becsülni az átlagos termikus sebessége az elektronok
Vegyük, amint az az elmélet a vezetőképessége Drude-Lorentz Ohm-törvény és a Joule. Egyszerűsítése becslések feltételezzük, hogy minden a vezetési elektronok azonos termikus sebességgel - U.
a. Ohm-törvény. Ha létrehoz egy mező E belsejében fém. a véletlenszerű mozgás az elektronok szuperponálódik mozgás irányított egy bizonyos átlagos driftsebesség v. Az áram a vezetékben rész S. I = enSv. n ahol a vezetési elektron sűrűség, e annak ellenében. Az áramsűrűség. (9.5)
Találunk az átlagos driftsebesség v. Feltesszük, hogy az elektron az erő EE időintervallumban t egy ütközés alapkristályának a másik mozog gyorsulás a sebesség és 0-ról. (9.6)
Mivel a mozgás egy elektron az elektromos mezőben egyenletesen gyorsuló, az átlagos sebesség felével egyenlő a maximális; (9.7)
és az elektromos áramsűrűség egyenlő. (9.8)
Egyenlet (9.8) kifejezi az Ohm-törvény differenciális formában az elektronikus elmélet. A együtthatója E dekódolja a makroszkopikus jellemzőit a vezeték, a vezetőképesség g sokaságán keresztül a mikroszkopikus elektron gáz.
Úgy becsüljük, az átlagos idő t szabad úthossza vezetési elektronok a példában a réz. Feltesszük, hogy az egyes a réz atom van egy szabad elektron. Ha a moláris tömege a réz, d sűrűsége, a sűrűsége a szabad elektronok. Helyett n expressziós vezetőképesség.
Az időintervallum t két ütközések elektron halad átlagos távolság, amely több tíz keresztirányú atomok.
Úgy becsüljük, az átlagos sebesség v az eltolódás a vezetési elektronok réz egy E térerősségű = 0,1 Inç M. tól (9.7) kapjuk:
A driftsebesség egy milliárd szer kisebb, mint a termikus sebesség u = május 10 m / s.
Megjegyezzük, hogy az intenzitás E = 0,1 V / m nem olyan kicsi, mint amilyennek látszik értéket. Ez megfelel a feszültséget 0,1 V-nál a végén a vezetékeket az 1 m. Ebben a feszültség keresztül rézdrót 1 mm S = 2 halad aktuális.
b. Joule-Lenz. Az elektron tömege több, mint ezerszer kisebb, mint a tömeg az atomok a kristályrácsban. Ezért, egy rugalmatlan ütközés egy csomópont leáll az elektron, a sebessége 0 lesz, és a kinetikus energia a sodródás teljesen adott csomóponthoz. Mivel idején ütközés (Forma 9,6), az által szállított energia elektronok egységnyi térfogatú egy másodperc egyenlő
Ez az energia szabadul fel hőt, így a képlet (9.9) kifejezi a Joule-hő differenciális formában. A kifejezés a vezetőképessége (9.10)
Kiderült ugyanaz, mint a képletben Ohm törvény (9,8).
Szigorúan véve a feltételezés, hogy az összes elektron feladja energiát, amikor összeütközött egy atom csak akkor érvényes, ha az atom nyugalmi állapotban. De az atomok rezegnek, és az ütközés nem teljesen rugalmatlan. Ezért az elektronok egyaránt energiát adnak (hatás a távozó atom), és fogadni (ütköztetés beeső atom). A statisztikák a termikus egyensúlyi körülmények átlagos elektron mozgási energia állandó hőmérsékleten állandó marad.
De amikor az elektron gáz lesz irányítva eltérési sebesség válik túllépése termikus mozgási energiája. Ez a nem egyensúlyi elektron energia energiával csomópontok. Ezért folyamatosan át rácspontjain, növelve a hőmérsékletet a karmester.
a. Wiedemann Franz törvényt. 1853-ban, a német és G.Vedeman R.Frants találtuk, hogy az arány a hővezetési a vezetőképessége g c ugyanezen a hőmérsékleten azonos minden fémek. A 1882godu dán fizikus Ludwig Lorenz azt mutatta, hogy ez vonatkozik-shenie arányos az abszolút hőmérséklet a Wiedemann-Franz törvényt. (9.11)
Itt L - együttható megegyezik az összes fém, ez az úgynevezett Lorenz számát.
Klasszikus elektron elmélet magyarázza a törvény.
Mivel az elektronok nagyon mobil, akkor feltételezhető, hogy a hővezető fém elsősorban a hővezetés az elektron gáz. A hővezető egyenlő (9,12)
Ott l - szabad úthossza elektronok, u - az átlagos termikus sebesség, i = 3 - a fokok száma szabad elektronok, k a Boltzmann állandó.
Behelyettesítve képletű (9,11) c a (9.12) és g (9.10), ahol t = lçu. kapjuk (9.13).
A kinetikus elméletét ideális gázok, az átlagos elektron sebessége hőmozgást U 2 = 8kTçpm. Ezért (9,14).
Klasszikus elektron elmélet általában igaz értelmezi a Wiedemann-Franz törvényt. Ez dekódolja a Lorentz-számot L = 8k 2 çpm kombinációjaként állandók, és lineáris függését cçg T hőmérséklet.
4. Nehézségek a klasszikus elektron elmélet. A fenti megállapítások tartoznak Drude és azok lettek, feltételezve, hogy az összes vezetési elektronok azonos sebességgel u termikus mozgás.
Henrik Lorenz megállapításokat tenni, amikor elfogadta az Maxwell elektron sebessége forgalmazás. Ennek eredményeként, a képlet Wiedemann Franz törvény megváltozott faktor helyett 8çp = 2,55 volt pontosan 2. Azonban a specifikáció a követelés volt a legrosszabb mérkőzés tapasztalat.
a.Molyarnaya fém hőkapacitás kell állnia a hőkapacitása a rács csomópontok 3R ideális gáz hőkapacitása és elektronok 3RZç 2, ahol z száma vegyérték elektronok az atom. Összesen hőkapacitás kapunk egyenlő 3R + 3RZç 2. De a tapasztalat ad 3R hő (törvény Dulong és Petit). A klasszikus elmélet nem magyarázza ezt.
A képlet vezetőképesség g = NE 2 l / 2mu szám szerinti átlagos sebessége u összhangban statisztikai elmélete az ideális gáz arányos a négyzetgyökével a hőmérséklet. Azóta u
. Ezért g = 1çr
. De a tapasztalat ad lineáris függését az ellenállás a hőmérséklet, vagy r
T. Az eltérés megmagyarázhatatlan.
Teljesen képtelen a klasszikus elektron elmélet magyarázza a jelenséget a szupravezetés. Ennek lényege, hogy egy bizonyos hőmérsékleten, az úgynevezett kritikus Tk, és közel abszolút nulla a legtöbb kémiailag tiszta fémek, ellenállása vezető hirtelen esik lényegében nullára. Úgy becsüljük, amelyeket a jelenlegi bomlási ideje egy szupravezető gyűrű, amely igazolja, hogy az ellenállása szupravezetők legfeljebb 10-25 ohm × m. Összehasonlításképpen, a fajlagos ellenállása a réz a normál állapotban egyenlő 1,7 × 10 -8 ohm × m.
A klasszikus elektron elmélete r
, ellenállás kell csökkenteni, monoton hőmérséklet, nincs folytonossági hiány.
5. A határok alkalmazhatóságának elektronikus elmélet. A klasszikus elmélet a vezetőképesség, annál nagyobb a szilárd anyagokat a kísérleti eredmény, az alacsonyabb hőmérséklet a vezeték, és minél magasabb a koncentráció a vezetési elektronok. Azokban az esetekben, ahol a hőmérséklet elég magas, T> Troom. és a hordozó koncentrációja alacsony, az elektronikus elmélet indokolt nemcsak minőségi, hanem mennyiségi becsléseket. Ez egy értékes lehetőség, hiszen a klasszikus elektron elmélete Drude-Lorentz sokkal egyszerűbb és világosabb kvantum elektron elmélet.
Vissza a tartalomjegyzék: