harmonikus oszcillátor
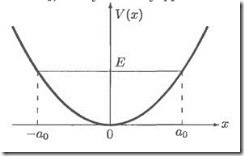
Nyilatkozat a problémát. Tekintsünk egy stacionárius állapot egy kvantum részecske tömege mozgó egy egydimenziós rugalmas potenciális energia területén, ahol a relatív merevségét. Az ábrán a teljes energia a részecske. A fordulópont, ahol a mozgási energia nulla, koordinátái [L1]
A Hamilton-rendszer formájában
Stacionárius állapot fogja meghatározni a következő megoldásokat a Schrödinger-egyenlet
Itt körfrekvencia bevezetjük egyenlet (S.2) folytassa a dimenzió nélküli változók. Ezután állítsa ahol a Hamilton (S.1) formájában
További megoldások spektrális probléma lehet folytatni a szokásos módon, közvetlenül megoldása az differenciálegyenlet. Mi volt azonban, különben miért használja az elképzelést, a teremtés és pusztítás [L2].
Ez az állítás nem hermitikus operátor. Hermitian adjoint üzemeltető formájában
Telefonközpont szereplők és
Másrészt
A véleménye szerint a modell Hamilton operátor a harmonikus oszcillátor veszi az egyszerű űrlapot
Itt bemutatjuk az üzemeltető
Így a Hamilton a rendszer- lineáris függvénye a kezelő oldat a probléma már csökken a spektrális meghatározását sajátfüggvények és sajátértékei a kezelő könnyebb.
Spectral probléma az üzemeltető:
Megvizsgáljuk a tulajdonságait az üzemeltető.
1. A sajátértékek nem negatív szereplő.
Sőt, feltételezve, hogy a funkciók normalizálják egység, azt találjuk,
az eltűnő a helyzet, ha ez következik a bizonyíték, hogy a spektrum az üzemeltető. és így a Hamilton-korlátos alábbiakban. Korlátozások annak a ténynek köszönhető, hogy az üzemeltető a potenciális energia legalább.
2. Tegyük fel, hogy a függvény egy sajátfüggvény a sajátérték. Meg lehet mutatni, hogy a
Így, ha ezt. Nyilvánvaló, hogy egy magánvállalkozó. és - a saját értéke. Ha a jóváhagyás kell 1
ahol - egy magánvállalkozó. megfelelő legkisebb sajátértéke. Mivel - a legkisebb sajátérték, összhangban az elfogadott 2. szerezni
Saját értéke is középértéke az üzemeltető képes:
Következésképpen a legkisebb sajátérték nulla.
4. A sajátértékek egészek.
Sőt, még - sajátértékek. fekvő intervallumban. és - a megfelelő sajátfüggvények. Mi jár következetesen időzíteni a funkció az üzemeltető. Az eredmény egy olyan szekvenciát sajátértékek :. Az utolsó ebben a szekvenciában sajátérték tartományokat. Ez megfelel egy privát funkciót. Alkalmazzuk az üzemeltetőt, hogy a funkciót. megkapjuk
Az eredmény annak a ténynek köszönhető, hogy a kereset az üzemeltető vezet sajátérték. ez nem lehetséges (lásd. 1. rész). Sajátérték -Ott átlagos értéke az üzemeltető képes:
Ezért arra a következtetésre jutottunk, hogy
Amikor - a legkisebb sajátérték.
5. Let - magánvállalkozó funkció saját értékek azt mutatják, hogy a funkció - szintén sajátfüggvény az üzemeltető a sajátérték Valójában a kommutációs kapcsolatban (S.6) kap
Mivel a határtalan üzemeltetői mozgási és helyzeti energia spektruma a felső korlátlan.
Az üzemeltetők nevezzük létrehozását és a megsemmisülés üzemeltetői részecskék, és az üzemeltető - úgynevezett részecskeszám üzemeltető. Az ilyen operátorok széles körben használják a különböző szakaszain a kvantummechanika. Az részecske nem kell figyelembe venni a valós részecske és kvantum energia
Hagyja sajátfüggvény a részecskék számát. majd
Következésképpen, a probléma a stacionárius állapot a harmonikus oszcillátor formájában
egy diszkrét energia-spektrum. amely adott (S.13) a formája:
A szám az úgynevezett főkvantumszámú. Energia-spektrum (S.15) egyenlő távolságra lévő, azaz a távolságot, és nem mindig attól a szomszédos szintjei
Vegye figyelembe, hogy a segítségével a teremtés és pusztítás az energia-spektrum által meghatározott megkerülve a azonnali megoldást a spektrális probléma (S.14), és amelyek csak a kommutáció kapcsolatban (S.6).
Határozzuk meg (S.14) saját funkcióit. Hisszük, hogy a eigenfunctions ortogonális és normált egység, azaz a
Hogy a kereset az üzemeltető a hullámfüggvény. mert
Factor kell meghatározni. Vegyünk egy skaláris szorzata
Mi meg az intézkedés az üzemeltető a funkciót. mert
Az eredmény
Mi jár, hogy meghatározzák a konkrét formája a hullám funkciók a stacionárius állapot a harmonikus oszcillátor. Ebben az esetben használjuk tulajdonságok (S16) és (S.17) megsemmisülés és a teremtés szereplők. Hogy oldja meg a problémát, először meg kell határoznia a hullámfüggvény. megfelel a legkisebb sajátértékei a hullámfüggvény a sajátértékek segítségével határozható meg az ingatlan (S.17) létrehozása üzemben. mert
adott kifejezett formában (S.4) a megsemmisítése az üzemeltető, megkapjuk a következő elsőrendű differenciálegyenlet
Itt van a normalizációs feltételt megkapjuk a többi funkciót, a tulajdonság (S.17) üzemeltetője Született:
Annak megállapítására, az eredmény az akció fokú született üzemeltető a hullám, amelyet a földi állam. Tekintsük a következő kifejezést. van
Átírása (s.20) formájában
Ezután helyettesíti a munkát a szereplők identitásának üzemeltető Ennek eredményeként megkapjuk
Az explicit formában az üzemeltető. Eljutunk egy terméket a piaci szereplők. azaz A termék az üzemeltetők Ennek eredményeként a kifejezés a hullám függvény az
vagy adott (s.19)
Végül a eigenfunctions a Hamilton a harmonikus oszcillátor felírható
Funkciók jól ismertek a matematika és az úgynevezett polinomok Chebyshova Ermita. Ezek a funkciók alkossanak ortonormális sor [L4]:
Végül visszatért a háromdimenziós változó megoldás a spektrális probléma (S.2), a formája
Kiszámítására különböző átlagos fizikai mennyiségek, szükségünk van a rekurzív sorozat a funkciók és képletek differenciálódásukhoz változó Ezek könnyű levezetni, ha használjuk a kifejezést (s.16), (S.17) létrehozását és a megsemmisülés szereplők. Tekintettel arra, hogy explicit formában, megkapjuk
Összehasonlítása klasszikus és harmonikus oszcillátor
1. A teljes energia a klasszikus harmonikus oszcillátor vehet minden pozitív érték, mivel. Amikor a részecskék nyugalmi a származási. A kvantum esetben az eredmény alapvetően eltérő. Az összes energia csak akkor diszkrét értékeket az energia spektruma egyenlő távolságra - független. A legkisebb értéke [l5] energia nevű nullpont energia.
2. Az átlagértékek a helyzet és lendület klasszikus oszcillátor egyenlő nullával: kvantum oszcillátor átlagos koordináta és az impulzus rendre:
Figyelembe véve a kifejezést (S.25 Melegvízkészítés), (S.26 Melegvízkészítés) talál
Itt feltételezzük, hogy a funkciók alkossanak ortonormált halmaz úgy, hogy
Így mind a klasszikus és kvantum oszcillátor jelent koordináták értékeit, illetve pulzus nullával egyenlő.
3. A modell a klasszikus harmonikus oszcillátor, az energia kapcsolatban van a szórás az egyensúlyi kifejezést
ahol a sáv jelzi az átlagos idő a oszcillációk végezzük ellenőrzésére, hogy ez az arány a kvantum esetben. Ennek kiszámolásához a következő képlet segítségével (S.25 Melegvízkészítés), (S.26 Melegvízkészítés), az átlagos négyzetes ingadozások koordináták tetszőleges állapotban. van
Figyelembe véve a kifejezés az energia spektrum (S.24), megkapjuk
Így a klasszikus és kvantum esetben közötti kapcsolat az energia és a szórások az egyensúlyi helyzetből ugyanaz.
4. A klasszikus oszcillátor egy tétel Virial. . ahol - az átlagos időtartama alatt a kinetikus energia a részecske oszcilláció. Mi az összefüggés az átlagos kinetikus és potenciális energiájának az oszcillátor tetszőleges kvantum állapot. Tekintsük az átlagos
Ezért, közvetlenül következik
Így a kvantum esetben az átlagos kinetikus energia egyenlő az átlagos potenciális energia. azaz viriáltétel tart.
5.1. Megbeszéljük néhány jellemzője a kvantum államok a harmonikus oszcillátor. Ábra. egy grafikon kvantum szinten és a potenciális energia. Vegyük például a kvantum energia szintjét a klasszikus esetben a részecske ilyen energia között ingadoznak a pontokat, és (fordulópontjai, ahol a kinetikus energia nulla lesz). Jelöljük az amplitúdó a rezgések révén, és meghatározzuk a valószínűsége, hogy egy részecske a területen. fekvő belül a szegmens.
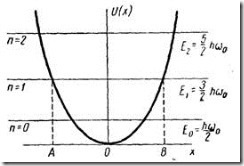
Ez a valószínűség
ahol az idő, amely alatt a részecske utazik távolságban időtartamra és az oszcilláció. Hagyja, hogy a határidő oszcilláció ezután
ahol - a részecske sebessége. Mi kifejezni a sebessége a részecskék egy változtatható az egyszerűség kedvéért, hogy a megoldás az egyenlet a mozgás a klasszikus oszcillátor van
Így a valószínűsége kért
A kifejezés előtt nyilvánvalóan a valószínűsége sűrűsége. Jelölje meg a
Megjegyezzük, hogy az elosztó (S.28) A normalizálás feltétel teljesül. A formája az elosztó (S.28) azt mutatja, hogy a funkció minimális a ponton. A fordulópont tehát a valószínűsége, hogy egy részecske a központi terület kicsi annak a ténynek köszönhető, hogy a részecske sebessége maximalizálva van a környéken, a forgási sebesség alacsony, és a valószínűsége, hogy egy részecske tovább.
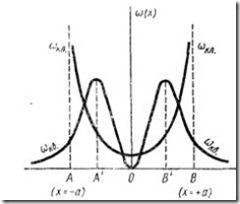
Tekintsük a harmonikus oszcillátor. A valószínűsége, hogy a részecske egy tetszőleges kvantum állapotban van
Az állami energetikai
Az eloszlás három pontot szélsőérték - minimum pont és két magas pontokat (a pontokat, és -kal). Hogy szinten a forgáspont és a koordinátákat fontos, hogy az eloszlás meghatározása és kívül a fordulópont, azaz a van egy nulla a valószínűsége a részecskék a régión kívül
5.2. Kiszámoljuk a szórás és a koordinátákat a pulzust egy tetszőleges kvantum állapot. Mivel az átlagos koordináta és az átlagos lendület kvantum oszcillátor nulla, van
Mi határozza meg a termék. van
Az alapállapot az arány a bizonytalanság valósul egyenlőség
azaz nullpont energia kevesebb energiát összeegyeztethető a határozatlansági reláció.
Így a határozatlansági reláció áll fenn a kvantumbit harmonikus ostsiilyatora
Alacsony hőmérsékleteken, az atomok egy molekulában vagy szilárd végre kis körüli ingadozás stabil egyensúlyi helyzete. Kísérleti vizsgálata fényszórás kristályok azt mutatta, hogy a hőmérséklet csökken, az intenzitása a szórt fény azokban nem nulla (mivel követi a klasszikus elmélet), és hajlamos arra, hogy néhány határérték, még a abszolút nulla hőmérséklet. A potenciális energia alacsony hőmérsékleten közel az egyensúlyi helyzet lehet közelíteni egy másodfokú potenciáljára, ezért harmonikus oszcillátor modell itt van egy jó közelítés. Figyelembe ebben a modellben nem pont létezését nullpont rezgések megfelelő alapállapot energiával
Végül, 5. bekezdés, tudomásul vesszük, hogy ez következik a vita, az alapállapot, hogy a következő, és vele a gerjesztett állapotok nagyon különbözik a klasszikus. Magasan gerjesztett állapotú. Ezzel szemben, kicsit más, mint a klasszikus.
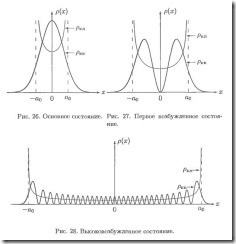
Általában, koordinálja a részecskeméret-eloszlás egy tetszőleges kvantumállapotban hullám funkciót. által leírt kapcsolatban (s.29). Az alapállapotú a részecskeméret-eloszlás a koordináták egy jól ismert valószínűségszámítás Gauss-féle eloszlás:
azt mutatja, hogy ebben az állapotban a részecskék lokalizálódik a központi régióban (- maximális pont). A klasszikus oszcillátor eloszlása, mint a kvantum esetben, és van egy nem nulla a valószínűsége a részecske kívül a lehetséges is. Annak a valószínűsége, exponenciálisan csökken a területen kívül, amikor az elosztó a kvantum részecske oszcillál erősen a régióban. A rezgési amplitúdója csökken, és az átlag megközelíti
kiválasztási szabályok. A sugárzás intenzitása a dipól és kvadrupól
Beszéljétek, anélkül, hogy részleteket, a probléma-kibocsátása a harmonikus oszcillátor. Ezt a problémát illusztrálja egy másik jellemzője kvantum rendszerek kapcsolódó úgynevezett kiválasztási szabályok.
Dipól átmenetek. Az intenzitás a spontán emisszió (azaz a sugárzási energia egységnyi idő) a felső réteg. A mélyen fekvő energia szinten az energia egyenlő
ahol a töltés a fény sebessége, együttesen egy mátrixot. Annak érdekében, hogy kiszámítható a mátrix elem használjuk a rekurzív sorozat a eigenfunctions
A kifejezést (s.35), ebből következik, hogy nullától eltérő csak azokat mátrix elemeinek (engedélyezett átmenetek), akik számára vagy. azaz A kiválasztás szabályait a kvantum állapot határozza meg a képlet:
A kiválasztási szabályok azt jelenti, hogy az átmenet csak akkor lehetséges, a szomszédos szinten.
Összhangban a kiválasztási szabályok az alábbi, nem-nullmátrix kapcsolatos elemeket dipólus átmenetek:
A frekvencia a sugárzás. kap
Mivel a spontán átmenetek lehetségesek fentről lefelé (), összhangban (S.34), hogy az intenzitás a harmonikus oszcillátor sugárzást találni
A régióban nagy kvantum számokat. és amikor (s.37)
tudjuk figyelmen kívül hagyják a nullpont energia kapott ez a kifejezés azonos formában klasszikus analízis eredménye a harmonikus oszcillátor sugárzás számára érthető az átlagos energia egy harmonikus oszcillátor a rezgési periódus