A modul a gyorsulás vektor egyenes vonalú mozgás gyorsulás görbe pályájú mozgás

A sebesség és az útvonal a mozgás:

a> 0 egyenletesen gyorsuló mozgás;

Probléma 2. A ferde sík a vízszintes összetevője a szög 30, mozog a test súlya 5 kg. Ez a szerv útján nyújthatatlan fonalat akasztott egész blokk test vonzódik azonos tömegű mozgó függőlegesen lefelé (ábra. 1). csúszás aránya a test és a ferde sík 0,05. Határozza meg a gyorsulás, a test és az erejét a fonal feszültsége.

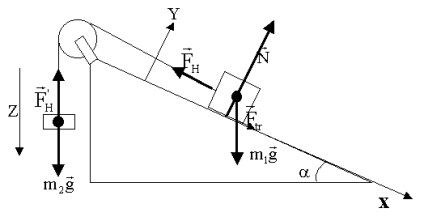
Határozat. Megmutatjuk az ábrán ható erők minden szervnek. Írunk az egyes szervek az egyenlet a mozgás (Newton második törvénye):

A kiemelkedések a kiválasztott koordinátatengelyek:

Tekintettel arra, hogy ha egy egyenletrendszert:

Kivonjuk a második egyenlet az első:

A kívánt gyorsulás:

Kiszámítjuk a gyorsulás a:

feszítőerő találtuk az első egyenletből:

Probléma 3. Keresse meg a lineáris gyorsulás a labdát súlypontok
és a meghajtó, csúszó csúszás nélkül egy ferde síkon. síkja dőlésszög 30. A kezdeti sebességét a szervek egyenlő nullával.

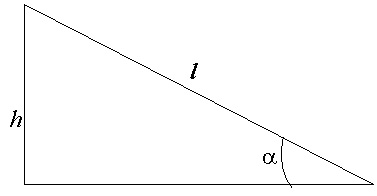
Határozat. Amikor gördülő a test egy ferde sík h magassága a potenciális energia alakul át kinetikus energia transzlációs és rotációs mozgást. A törvény szerint az energiamegmaradás:

ahol - a tehetetlenségi nyomaték, m - tömeg.

A hossza a ferde sík l van társítva a magasság a kapcsolatban (2. ábra):

A lineáris sebesség társul egy szöglet:

Miután helyettesítése (2) és (3) az (1), kapjuk:

Mivel mozgás alapján történik, állandó erővel (gravitációs), a mozgás szervek - egyenletesen gyorsult. ezért:

Megoldása (4), (5) és (6), kapjuk:

Behelyettesítve a kifejezés a tehetetlenségi nyomaték a (7) képletű, kapjuk:

7.2. Elektromosság és mágnesesség

7.2.1. Magyarázat a munkaprogram

Tanulmány elektrodinamika alapítványok hagyományosan kezdődik az elektromos mező a vákuumban. A teljesítmény jellemző az elektromos térerősség, az energia - potenciális . Figyelmet kell fordítani a kapcsolatot. Számítani a kölcsönhatás erő a két díjat és pontos kiszámítását az elektromos mező által létrehozott ponttöltés szükséges, hogy képes legyen használni Coulomb törvény. Kiszámolásához a térerőt generált kiterjesztett díjak (feltöltött végtelen, repülőgép, stb), alkalmazza Gauss tétel. Egy olyan rendszer elektromos töltések szükséges alkalmazni a szuperpozíció elve (feladat ellenőrzési munkát 201-220).

A tanuló a témát „DC” kell tekinteni minden formáját Ohm-törvény és a Joule. Az ellenőrzési munka a feladat 221-230. A vizsgálatok „mágnesesség” kell venni, hogy a mágneses mező által generált mozgó töltésekre és hat a mozgó töltésekre. Itt meg kell figyelni, hogy a törvény a Biot-Savart-Laplace. Tudnunk kell, hogy a törvény, és tudja, hogyan kell használni, hogy kiszámítja a mágneses indukció - a fő jellemzői a mágneses mező (a kontroll munka a feladat 231-240). Különös figyelmet kell fordítani a Lorentz-erő, és megvizsgálja a mozgását egy töltött részecske mágneses mezőben (feladatok 241-250). A tanulmányozzák az elektromágneses indukció meg kell tanulni, hogy a mechanizmus az indukált elektromotoros erő van elektronikus jellegű. Az alaptörvény az elektromágneses indukció - ez a törvény a Faraday-Lenz. E törvény szerint, az EMF indukált a zárt hurokban történik, amikor a mágneses fluxus kapcsolódik az áramkör. Tudni kell, hogyan kell kiszámítani a mágneses fluxus által indukált elektromotoros számított mozgásáért zárt hurok áram mágneses mezőt és mágneses mező energia (az ellenőrzési feladatokat 251-260).

Elektromos és mágneses jelenségek egy speciális formája a fennállásának kérdése - az elektromágneses mezőt. Az alapja az az elmélet az elektromágneses mező elmélete Maxwell.

A programban nagy figyelmet fordítani, hogy a tanulmány a Maxwell-egyenletek. Ezek az egyenletek írhatók két módja van: a szerves és eltérés. Maxwell-egyenletek megfelelnek a relativitás elve: ők invariáns Lorentz transzformációk. A fő következménye Maxwell elmélete az következtetést a elektromágneses hullámok létezését, szaporító a fény sebessége.

7.2.2. alapképlete

ahol - az érték a lényeg díjak,

izotróp közeg (= 1 vákuum ),

r - a távolság a díjakat.

Az elektromos térerősség:

ahol - a ható erő ellenében,

a ponton helyezkedik a pályán.

A térerősség R távköznyire
a területen forrás:

végtelen hosszú töltésű

fonalak lineáris sűrűsége zaryada :,

egyenletesen töltött végtelen

sík felületi sűrűsége

két ellentétes töltésű

A potenciális elektromos mező,

ahol W - potenciális energiája a díjat.

A potenciális ponttöltés területen.

tölteni rasstoyaniirot.

Szerint a szuperpozíció elve mezők, feszültség:

ahol - a feszültség és a potenciál ebben a

pontja a mező által termelt i-edik töltés.

A villamos térerősség a mozgás

zaryadaqiz pont a potenciális pontnál

A kapcsolat intenzitása és a potenciális

inhomogén mező :,

a homogén mezők :.

Elektromos kapacitás félreeső vezető :.

Elektromos kapacitás lakás kondenzátor:

ahol S - területe a lemez (egy) a kondenzátor,

d - a távolság a lemezek között.

Az energia egy feltöltött kondenzátor :.

ahol S - a keresztmetszeti területe a vezeték.

 - ellenállás; l - hossza a vezeték;

S - a keresztmetszeti területe.

a homogén rész láncok

differenciális formában. .

jövesztőlánc tartalmazó EMF :,

ahol  - EMF áramforrás,

R és R - a külső és a belső áramkör ellenállását;

A zártláncú :.

a homogén része a DC áramkör:

ahol Q - mennyisége felszabadult hőtől a vezetékek

t - idő az aktuális;

lánc része, amelyben egy változó aktuális idővel:

Kommunikációs mágneses indukció

és a mágneses térerősség:

ahol - a mágneses indukció vektor

 - mágneses permeabilitása izotróp közeg,

(= 1 vákuum ),

- mágneses térerősség.

Mágneses indukció (mágneses indukció):

a közepén egy kör alakú áram

ahol R - sugara a kör alakú áramnak,

területein végtelenül hosszú egyenáram

ahol r - legrövidebb távolság a vezeték tengelyével;

mező által termelt vezetőszegmensen

ahol - közötti szög a vonalszakasz és egy vonal vezetőt,

összekötő szegmens végeit, és egy mezőt pontot;

mező végtelen hosszú szolenoid

ahol n - a menetek száma egységnyi hossza a mágnesszelepet.

ahol - az erő a díjat mozgó

mágneses térben,

- hiteldíjának q,

 - közötti szög a vektorok.

Az áramlás a mágneses indukció (mágneses fluxus révén ploschadkuS):

egy egyenletes mágneses mezőt,

ahol  - közötti szög a vektor és a szokásos, hogy a helyszínen

Egy inhomogén mezőben.

Flux (teljes áramlás):

ahol N - több tekercs fordul.

ahol - EMF indukció.

ahol L - induktivitása az áramkör.

ahol n - száma tekercsmenetet egységnyi hosszán,

V - a hangerőt a mágnesszelepet.

mágneses mező energia :.

A töltés folyik a zárt áramkörben

változó mágneses fluxust a áramkör:

ahol - a változó mágneses fluxus,

R - az áramkör ellenállása.

A munka halad a zárt

tokomIv mágneses mezőt:

7.2.3. Példák járó problémák megoldása elektromosság és mágnesesség

Probléma 1. Két egyenlő negatív töltés 9 NC vannak a vízben a parttól 8 cm-re egymástól. Annak megállapításához, a térerő és az esetleges olyan ponton 5 cm-re a díjakat.

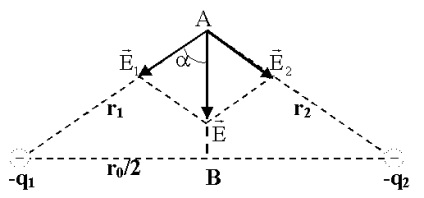
Határozat. A térerősség A pontban (. 3. ábra) által a szuperpozíció elve alapján is:

A tétel az koszinuszok:

Kaland ponttöltés területeken:

By hipotézis tehát. majd:

és az eredő erő egyenlő:

Jelöljük AB = h. Aztán.

A tétel Pitagorasz:

 kapott mező potenciál a pont egyenlő:

A potenciális által gerjesztett ponttöltés egyenlő:

De az állapotot. Majd így:

A: E = 480 V / m;  = -40 V.

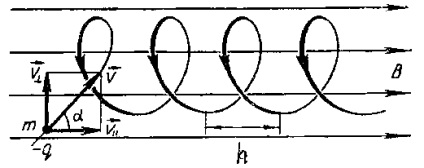
Adachi 2. elektron felgyorsul a potenciál-különbség 6 kV, legyek
egy homogén mágneses mezőt szögben 30 a mező irányát és elkezd mozogni egy spirális. Indukciója a mágneses mező B =. Keresse meg a sugár a menetek és a pályán a spirál.

Keresés: R, h. Ábra. 4

Határozat. elektron sebessége találtak a feltétellel, hogy a működése az elektromos erőtér költik a változás kinetikus energia az elektron:
A = W. A munka az elektromos mező megegyezik a termék a töltést a potenciális különbség: A = qU. A kezdeti kinetikus energia nulla, ezért W = W. Ezért:

Bővítjük az elektron sebessége, belép a mágneses mező két összetevőből áll: - a sebesség-összetevője mentén irányul erővonalak, és - a sebesség komponenssel merőleges a erővonalak. Ábra. 4:

A vetítés a elektron pályája a merőleges síkban, egy kör, ezért a Lorentz-erő említett szokásos részecske (centripetális) gyorsulás. Lorentz erő:

ahol R - a kör sugara.

Szerint a Newton második törvénye: F = ma.

kezelés időtartama:

Mivel a részecske sebességének van egy összetevője, a részecske pályája egy spirál.

helix pályán:

Ellenőrzése méretek számítási képletek (2) és (3).