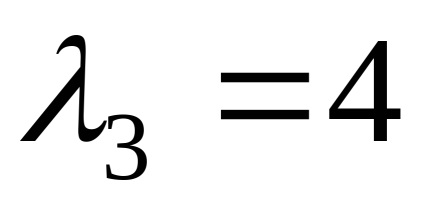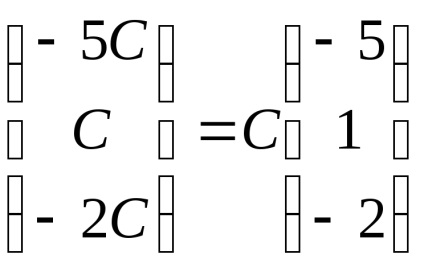Sajátvektor és sajátérték
Miután megoldotta ezt az egyenletet tekintetében



Tekintsük néhány példát, amelyek mindegyike elvégzi a menete a probléma megoldásának a megállapítás a sajátvektor és sajátérték.
Keresse meg a sajátvektor és sajátérték
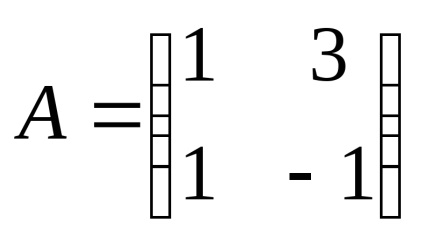
A mátrix a 2. dimenzió

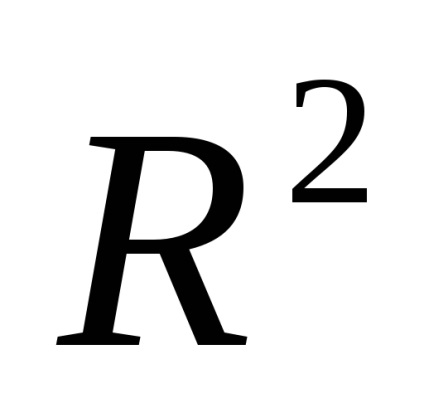
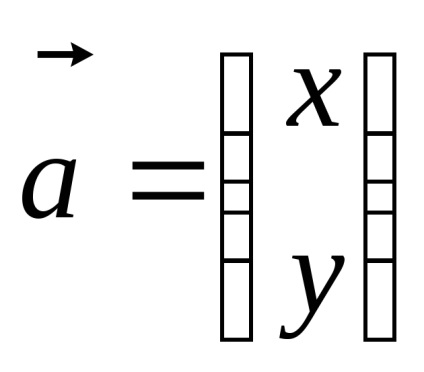
Létre kell hozni egy egyenlet megtalálása sajátvektorok a mátrix formában:
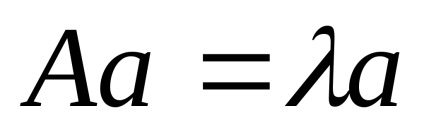

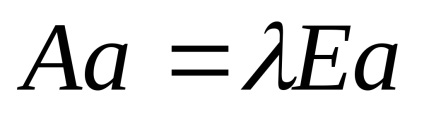

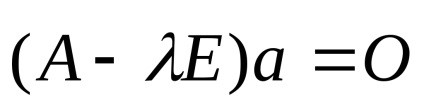
3. átírni az egyenlet mátrix formában az egyenletrendszert:
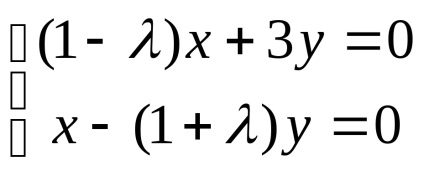
Homogén rendszer nem-triviális megoldásokat, ha, és csak akkor, ha a meghatározó a fő mátrix értéke 0. megkapjuk a karakterisztikus egyenlet a rendszer, és megoldani azt:
.
sajátértékei

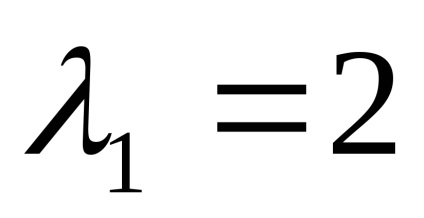
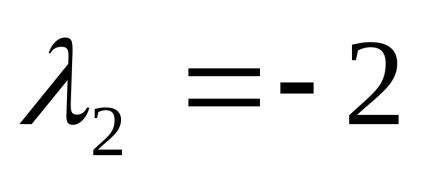
Találunk sajátvektorok mindegyik saját értékeit:
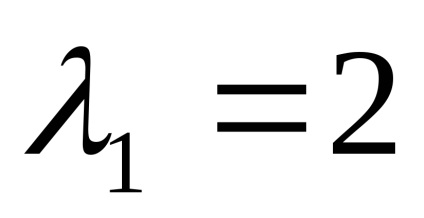
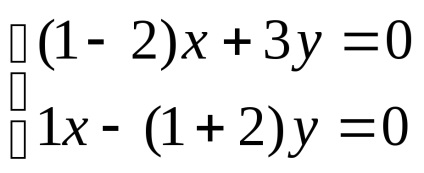
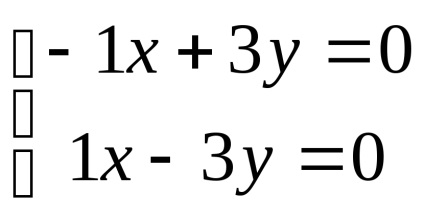
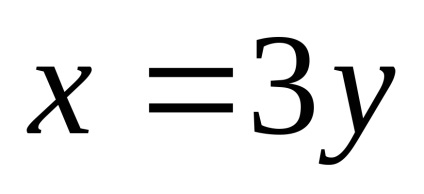
enged
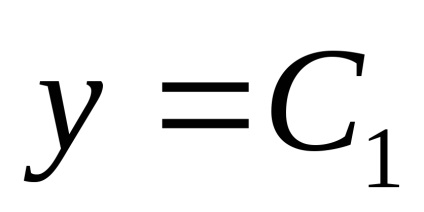

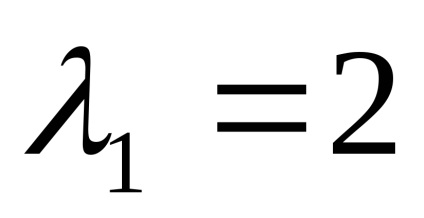
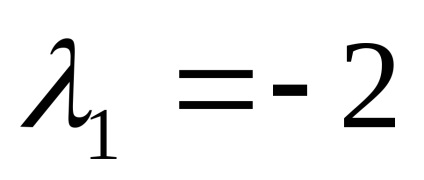
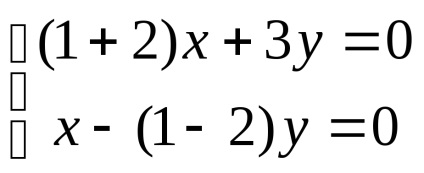
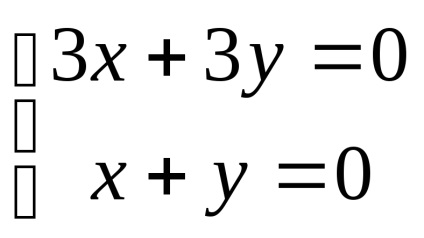
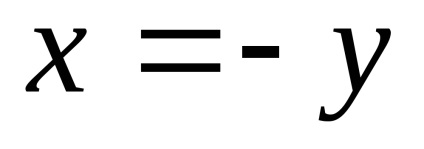
enged
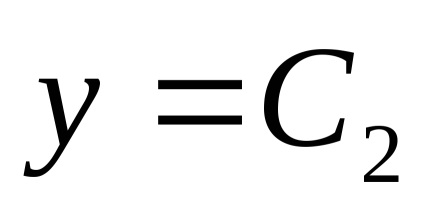

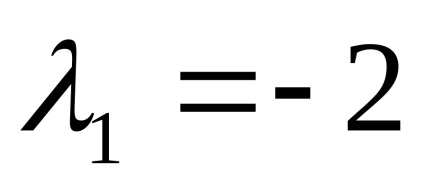
Példa 2. Keresse meg a sajátvektor és sajátérték egy lineáris operátor. bizonyos, előre meghatározott alapon matritseyA =
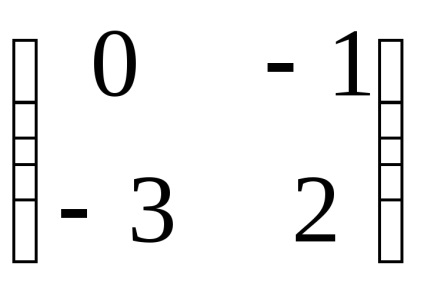
Összetétele és megoldani a karakterisztikus egyenlet
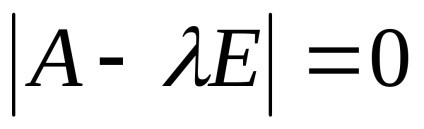
Ezután a karakterisztikus egyenlet formájában:
,
,
- sajátértékei lineáris operátor.
Találunk sajátvektorok megfelelő sajátérték
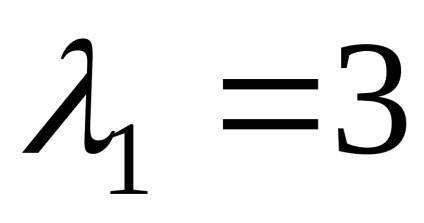
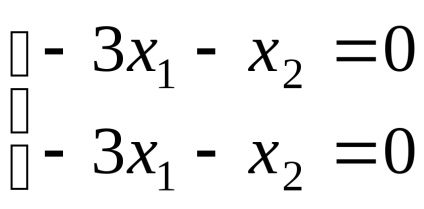
Elhelyezés a múlt egyenlet
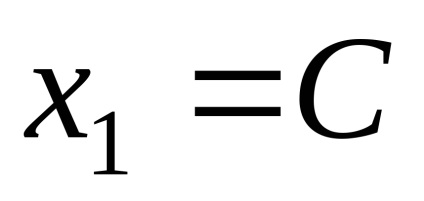
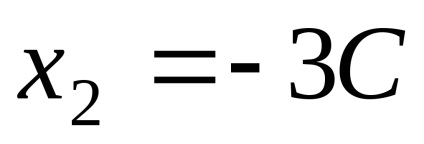
Hely sajátvektorok megfelelő sajátérték
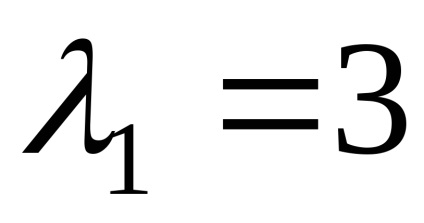
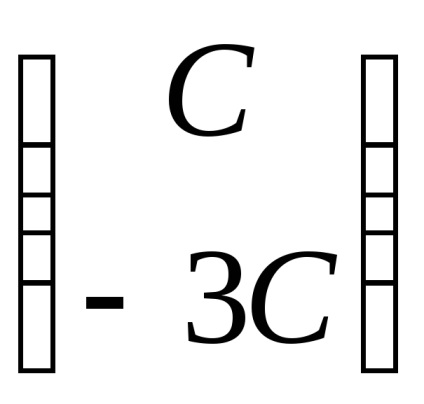
Találunk sajátvektorok megfelelő sajátérték
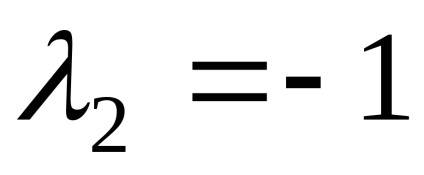
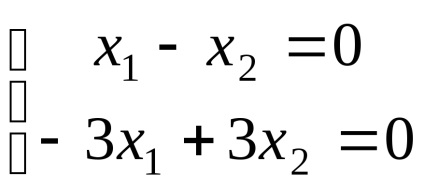
Elhelyezés a múlt egyenlet
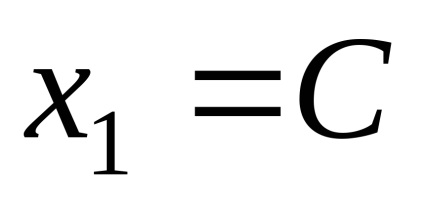
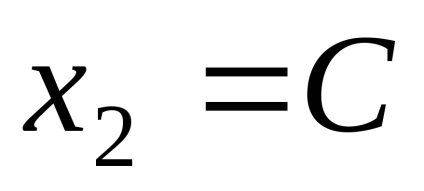
Hely sajátvektorok megfelelő sajátérték
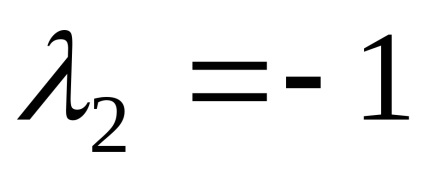
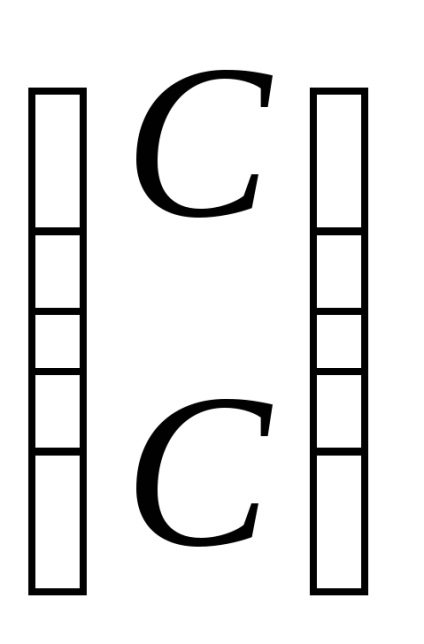
Válasz. sajátérték
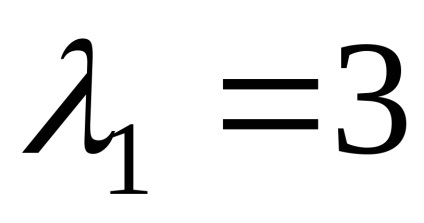
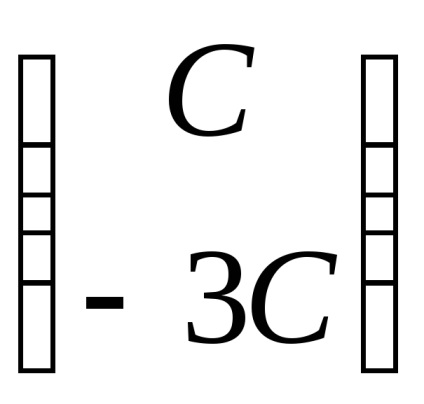
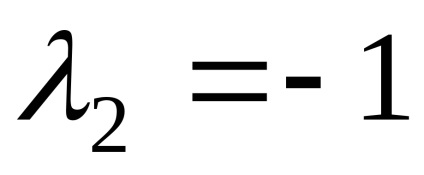
Példa 3. Keresse meg a sajátvektor és sajátérték egy lineáris operátor. bizonyos, előre meghatározott alapon matritseyA =
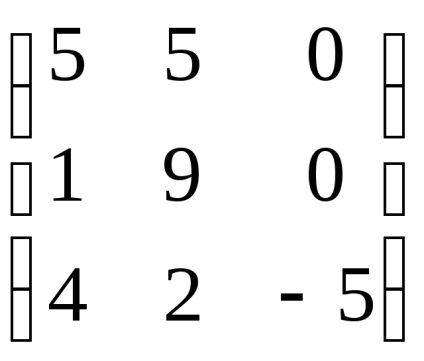
Találunk sajátértékei lineáris operátor. Ahhoz, hogy ezt elérjük, állítsa össze a karakterisztikus egyenlet és megtalálja a gyökereit:
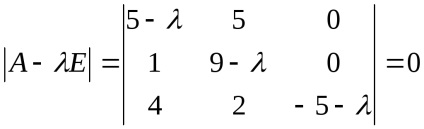
,
,
,
,
, ,
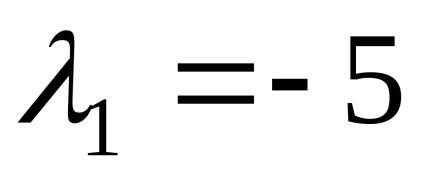
Találunk sajátvektorok megfelelő sajátérték
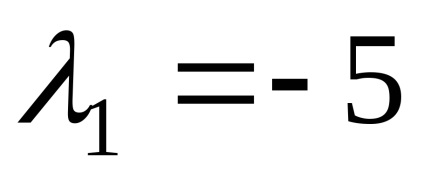
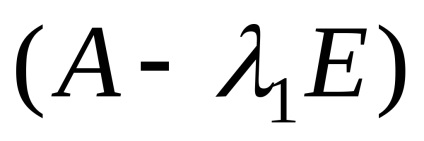
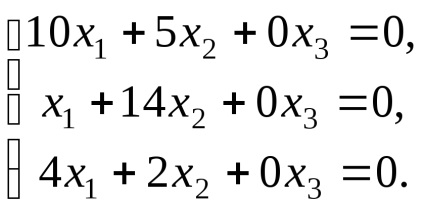

Mivel a rangot a rendszer mátrix (r = 2) kisebb, mint az ismeretlenek száma, a rendszerben van egy végtelen számú megoldást. Írásban transzformált rendszer megoldására, megkapjuk
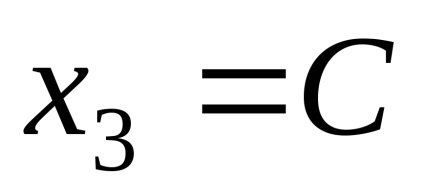
Így a sajátvektor megfelelő sajátérték
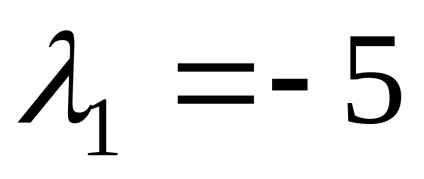
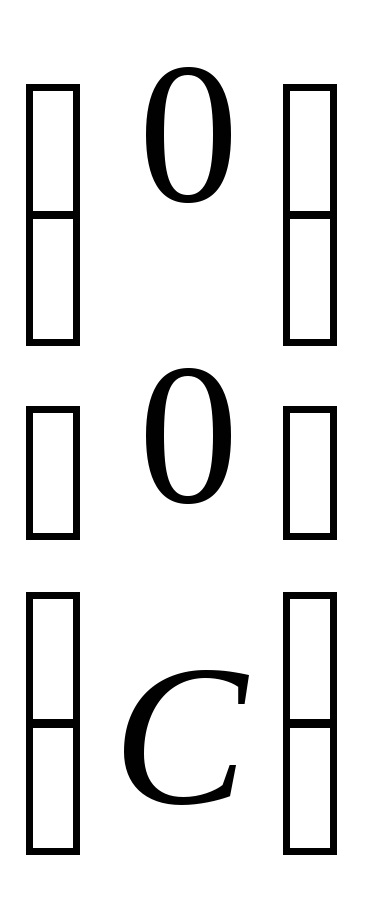
Találunk sajátvektorok megfelelő sajátérték
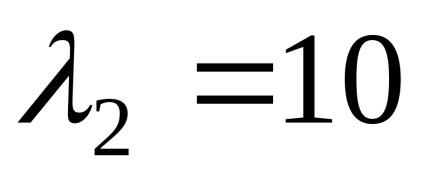
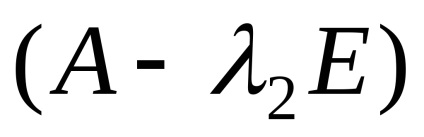
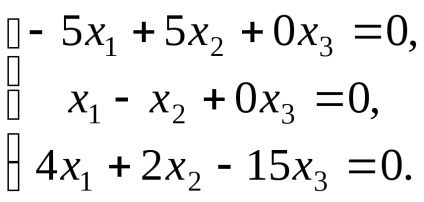
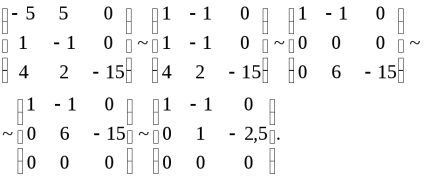
ahol a rendszer formájában
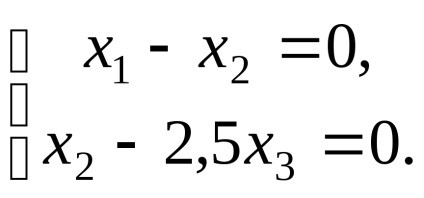
Így a sajátvektor megfelelő sajátérték
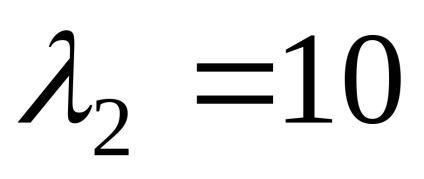
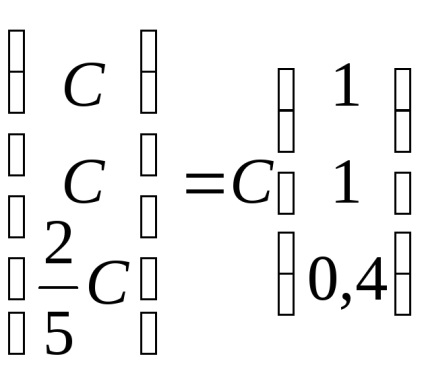
Találunk sajátvektorok megfelelő sajátérték
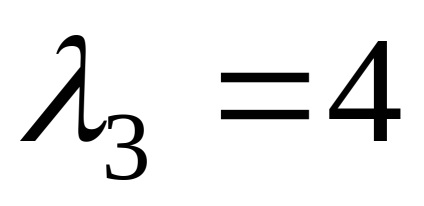
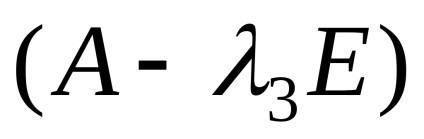
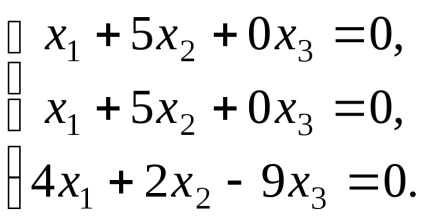
,
ahol a rendszer formájában
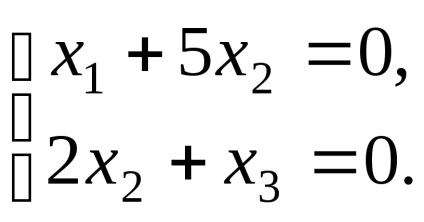
Így a sajátvektor megfelelő sajátérték