WolframAlpha orosz, hogyan kell felépíteni egy függvény grafikonját a wolfram, alfa
Kezdjük egy egyszerű építési két-dimenziós grafikon: plot sin (sqrt (7) x) + 19cos (x) x -20 20
Ha a 7 (-7), megkapjuk a grafikonok a valós és képzetes része a funkciók: plot sin (sqrt (-7) x) + 19cos (x) x -5 5
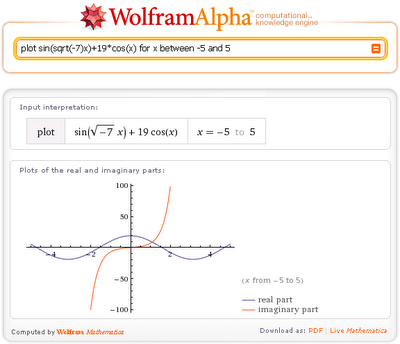
Az előző két példában, mi meg a domain értékeit érv x. És mi fog történni, ha nem adja meg a tartomány az x?
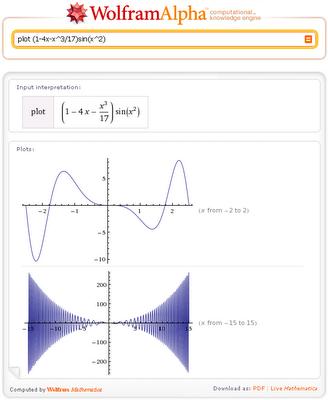
Az egyik különlegessége a Wolfram | Alpha az automatikus kiválasztása a megfelelő tartománya x ábrázolási függvények egy vagy két változó, például, ábrázoljuk ezt a funkciót tartalmazó Bessel függvények:
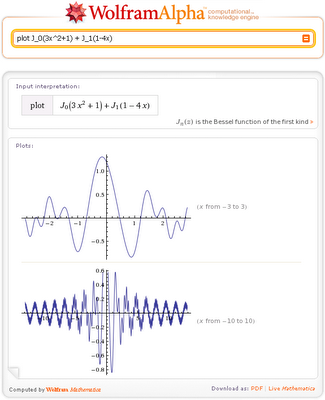
Ami a Wolfram | Alpha, hogy állítson össze egy függvény grafikonját, mindig előtag használatára telek. Ha belépünk bármely egydimenziós cselekmény nélkül előtag kifejezést. megkapjuk a függvény grafikonját kivéve derékszögű koordinátákkal, az is egy csomó más információ ezt a funkciót.
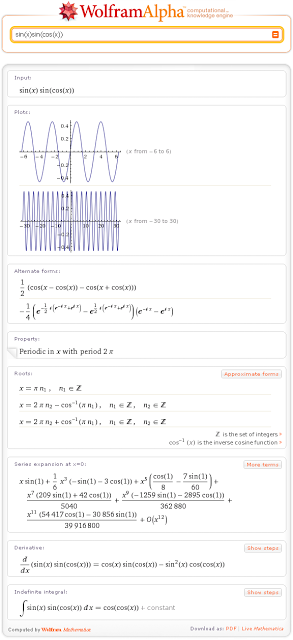
Ezen felül, a kép ábrázolási nagyobb lesz, ha olyan cselekmény előtagot.
Ezzel párhuzamosan, a Wolfram | Alpha képes grafikonok számos funkciót.
Most, hogy hogyan lehet Wolfram | Alpha ábrázolni feladatokat a két változó. Kezdjük a funkciója y ^ 2 cos (x) x, -6 és 6, és y -2 és 2
Csakúgy, mint az egydimenziós esetben Wolfram | Alpha automatikusan meghatározza a megfelelő értéktartománya az érvelés, ahol a függvény a legjellemzőbb formája. Ha Wolfram | Alpha nem találja a megfelelő tartományban, akkor valószínű, mert a rendszer nem tudta meghatározni egy sor, ahol a függvény a legérdekesebb viselkedést. Ebben az esetben tudjuk meg a tartomány kézzel, ahogy ez a fenti. Nézd meg a következő példákat:- plot sin (x cos (y))
- plot (x ^ április 05-04 x ^ y ^ 2 + x y - 1) / (y ^ 11 - x ^ 11 + 34 x ^ 3y + 1)
- plot (1 - x) / (2 x + 7, y), 5 x ^ 2 - 3y ^ 2 + 7 xy, (x + 2 y) ^ 4
- plot sqrt (1 + x y), sqrt (x ^ 2 - y ^ 2 + 2 x y)
- plot sin (x + I y)
- plot sqrt (y ^ 2 + 4 y) - sqrt (-I x ^ 3 + 3 x)