Learning mátrix-transzformációt CSS
Mátrix függvények - mátrix () és matrix3d () - két legrejtélyesebb szempontjából megértéséhez Gadgets a CSS3-transzformációk. A legtöbb esetben az egyszerűség kedvéért és az egyértelműség, akkor előnyös a funkciók, mint például forgatás () és skewY (). De még mindig az azonos mátrix mögött minden átalakulás. Hasznos, bár egy kis megértést, hogyan működnek, ezért vessünk egy pillantást.
Ebben a cikkben, azt fedett milyen a mátrix 3 3, használt kétdimenziós átalakítása és a mátrix 4 4 háromdimenziós.
Ebben a cikkben azt is figyelembe besprefiksnymi változat transzformáció tulajdonságait. A gyakorlatban ezek a tulajdonságok még csak kísérleti változhat. Mindaddig, amíg nem hagyták jóvá véglegesen, add a CSS-kódot változat előtaggal (pl. O-transzformáció).
Mi az a mátrix?
Mátrix - egy hűvös matematikai kifejezés egy téglalap alakú tömb számok, szimbólumok és kifejezések (lásd 1. ábra ..). A mátrix meghatározott matematikai és tudományos alkalmazások. Fizika, például azok használatát a tanulmány a kvantummechanika. A területen a számítógépes grafika használnak ilyeneket - hirtelen! - lineáris transzformációk és az előrejelzések a háromdimenziós képek kétdimenziós képernyőn. Ez az, ami a mátrix funkciók: mátrix () lehetővé teszi számunkra, hogy hozzon létre egy lineáris transzformáció, és matrix3d () lehetővé teszi, hogy a látszatot keltik, háromdimenziós két dimenzióban CSS segítségével.
Ábra. 1. példa mátrix
Nem fogunk vándorolni messze a mélybe a fejlett algebra. Meg kell ismernie a derékszögű koordináta rendszerben. Azt is frissíteni a memóriát, mint egy többszörösen mátrixok és vektorok (vagy használja a számológépet. Típus javasolt Bluebit.gr).
Fontos, hogy megértsük a pillanatban -, hogy megsokszorozza mátrix transzformáció a pont koordinátáit (vagy pont) kifejezett vektor.
Átalakítás és koordináta-rendszer
A transzformáció alkalmazható az objektumot, akkor létrehoz egy helyi koordinátarendszerben. Alapértelmezett Start helykoordináták - (0,0) - központjában fekszik a tárgy, vagy 50% a szélesség és 50% a magasság (2. ábra).
2. ábra. A helyi koordinátarendszerben.
Meg tudjuk változtatni az eredete a helyi koordinátarendszer beállításával tulajdonságait transzformációs eredetű (3.). Beállítása a transzformáció-eredetű. 50 képpont 70 képpont;, például elhelyezi a származási 50 képpont a bal széle a tárgy és 70 pixel a tetején. Átalakulása az egyes pontok a helyi koordinátarendszerben az objektum viszonyítva számítjuk ennek eredetét.
Ábra. 3. A helyi koordinátarendszer eredetére pontban (x 50, 70 képpont). pont (30px, 30px) is látható.
A böngészők érted ezeket a számításokat minden alkalommal, amikor alkalmazni az átalakulás. Csak azt kell tudni, hogy milyen érvek segítségével a kívánt hatás eléréséhez.
transzformációs számításban matematika mátrixok és vektorok
Nézd egy példa segítségével egy 3 * 3 mátrix kiszámításához egy kétdimenziós transzformációs (ábra. 4). A mátrix 4 4 használnak háromdimenziós transzformációk, működik az ugyanaz, a további számokat adunk a Z tengelyre
Ábra. 4. A kétdimenziós mátrix CSS-transzformációs
Mi lehet írni ezt a transzformáció: a mátrix (a, b, c, d, e, f), ahol a betűk a-tól f - szám típusa határozza meg az átalakulás, hogy szeretnénk alkalmazni. Mátrix - egy recept az ilyen jellegű átalakításokat szeretnénk alkalmazni. Lenne egy kicsit világosabb, ha megnézzük néhány példát.
Amikor alkalmazni egy kétdimenziós átalakulás, a böngésző megszorozza mátrix vektor [x, y, 1]. Az x és y - koordinátáit egy adott helyen a helyi koordinátarendszerben.
Ahhoz, hogy megtalálja a koordinátákat a transzformáció után, megszorozzuk minden eleme minden sorban a mátrix megfelelő vektor vonal. Ezután adja ki a terméket (ábra. 5).
Ábra. 5. mátrix és egy vektor
Tudom, hogy úgy néz ki, mint egy rakás értelmetlen számok és betűk. De, mint már említettük, minden típusú átalakulás - saját mátrixban. Ábra. A 6. ábra egy mátrix transzformáló műszak.
Ábra. 6. műszak mátrix
Értékek tx és ty - értékeket, amelyeket át kell helyezni a származás. Azt is biztosítani azt egy vektorba [1 0 0 1 TX ty]. Ez a vektor egy argumentumot funkció mátrix (). az alábbiak szerint.
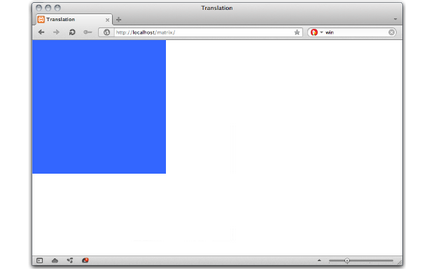
Ábra. 7. Egy tárgy a globális koordinátákkal (0,0).
Mi lesz az objektum áthelyezése 150 képpont mentén x és y tengelyek, a koordináta transzformáció alapértelmezés szerint. Az alábbiakban a CSS ez az átalakulás.
By the way, ez egyenértékű azzal, hogy átalakítsa: lefordítani (150px, 150 képpont). Nézzük az eredmény kiszámítása ennek az átalakulásnak a pont koordinátái (220px, 220px) (8.).
Ábra. 8. kiszámítása a nyírási átalakulás.
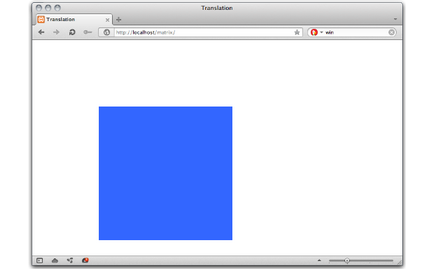
Ábra. 9. A létesítmény alkalmazása után az átalakulás.
nyírási Mátrix - egy különleges eset. Ő adalék. és multiplikatív. Egy egyszerűbb megoldás lenne, ha egyszerűen csak hozzá az eltolás értékét értékeinek x és y koordinátája a pontokat.
Kiszámítása a háromdimenziós transzformációs
Megvizsgáltuk a átadása a mátrix 3 által 3. Vegyünk egy másik példát, használva egy sor 4 4 a skála (ábra. 10).
Ábra. 10. A mátrix 4 4 méretarányosak.
Itt sx. sy és sz képviseli léptéktényezőket minden tengelyen. A funkció matrix3d fog kinézni: transzformáció: matrix3d (sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1).
Mi továbbra is ugyanazzal a tárgy, mint korábban. Csökkentik a skála a x és y tengelyek segítségével matrix3d () függvény. az alábbiak szerint.
Ez egyenértékű azzal, hogy átalakítsa: scale3d (0,8, 0,5, 1). Ahogy beállítjuk csak az x és y (fogadó 2D-transzformáció), mi is használni, hogy a transzformációs: mátrix (.8, 0, 0 5, 0, 0), vagy skála (.8, .5). Az eredmény az átalakítás úgy is ábrán látható. 11.
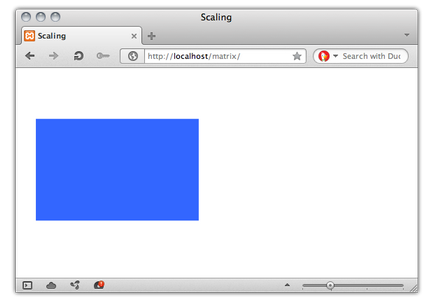
Ábra. 11. A tárgy a 300 300 pixel alkalmazása után a méretezési transzformációt.
Ha megszorozzuk ezt a mátrixot, hogy koordinálja vektor [150,150,1] (. 12. ábra), megkapjuk az új koordináták mi szempontunkból: (120,75,1).
Ábra. 12: a skálázás számítása átalakulás.
Hol kap a mátrixok
Az értékek a transzformációs mátrixok minden egyes funkció látható a Scalable Vector Graphics leírás. és a CSS átalakítja leírás.
Kompozit transzformáció a mátrix
Végül nézzük meg, hogyan lehet létrehozni egy összetett transzformáció - átalakulás egyenértékű használata több transzformációs függvények egyszerre. Az egyszerűség kedvéért korlátozzuk magunkat két dimenzióban. Ez azt jelenti, hogy fel fogjuk használni a transzformációs mátrixot 3 3 mátrix és () függvény. Ez az átalakulás fordulunk a tárgyat 45 ° és bővítsük a 1,5-szerese az eredeti méretét.
rotációs mátrix, kifejezve a vektor - [cos (a) sin (a) -sin (a) cos (a) 0 0], ahol egy - szöget. Szükségessége méretezés mátrix [sx sy 0 0 0 0]. Hogy összekapcsolják őket, akkor szorozzuk meg a forgatási mátrix léptékezek mátrix ábrán látható. 13 (szinusz és koszinusz 45 ° egyaránt 0,7071).
Ábra. 13: számítása a mátrix kompozit átalakulás.
A CSS-ben fog kinézni: transzformáció: mátrix (1,0606, 1,0606, -1,0606, 1,0606, 0, 1). Ábra. A 14. ábra az eredmény alkalmazása után az átalakulás.
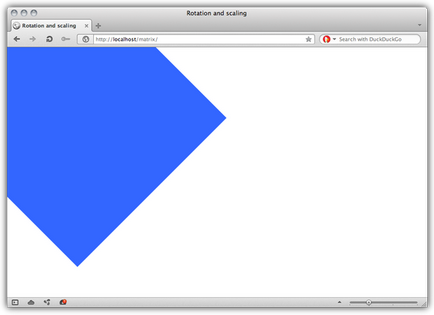
Ábra. 14: 300 Célunk 300 pixel után átméretezés és az elforgatás.
Ábra. 15. Az átalakulás.
Új koordinátáit a pontok (199.393px, 432.725px).
Ui Azt is érdekelhetnek:
Kevesebb, mint hat hónappal a legutóbbi változás W3C munkafolyamatban, mint a vezető a konzorcium kapott javaslatot, hogy ezt az új eljárást végül az ügyben. És írd le lényegtelen HTML specifikáció a múzeumban, így nem zavart a fejlesztők, „mintha” kapcsolódnia.
Tovább CSS modul, mely azt mondták csendesen érett állapotát, amellyel a W3C azt tanácsolja, hogy indítsa el a rutinszerű használata az új termékek. tartalmazzák a tulajdonság lehetővé teszi, hogy korlátozzuk a változás a fa rajz, újrarajzoláskor CSS-dobozokat, és változtatni a méretét az elemen belül. Ezért olyan fontos, ...
TÖBB
Paris (a képen), amely a közelmúltban elfogadott CSS munkacsoport ülésén, megérkezett szórakoztató hírek: Properties grid-row-rés és rács-oszlop-szakadék, valamint a csökkentés rácsos rés ...