Matrix exponenciális, matematikai problémamegoldás
Készítsen egy mátrix exponenciális mértékben, azaz a találni, ahol. Az összetett sajátértékek.
Terv: megtalálni a saját rendszer megoldást a kezdeti feltételek. és felkutatott és mátrix exponenciális egy mátrix, ha ezek az egyedi megoldások vannak írva oszlopok.
megoldás:
Kezdjük azzal, hogy megtaláljuk a sajátértékei ez a mátrix:
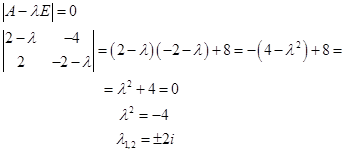
Most azt látjuk, a sajátvektorok:
1)
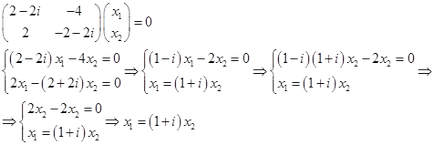
Ezután a sajátvektor ebben az esetben megtesszük:
A második sajátvektor minket ebben az esetben feleslegesen, mindig mindent kettős. Mi továbbra is.
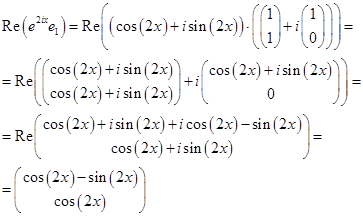
Ezután, az általános megoldás a rendszer differenciálegyenletek
valósítja meg:
És találunk egy különleges megoldás, hogy a kezdeti feltételek és.
1). helyettesíti az általános megoldás:
És az adott oldat formájában:
2). helyettesíti az általános megoldás:
És az adott oldat formájában:
Mi összerakható saját megoldásokat az oszlopok:
A vizsgálatot el lehet végezni a juhar, azaz kiszámított Maple mátrixban exponenciális.
Ez kezdeni, hogy csatlakoztassa a könyvtári funkciók lineáris algebra:
> A (linalg);
És akkor itt is írni:
> Exponenciális (, x);
Maple kapsz ezt:

Amely egybeesik a választ.