Alapoz egy egyenes vonal egy sík térbeli
Opr1. Vektor, az úgynevezett bázis egy L vonalat, ha a vektor, || L felírható
Opr2.Dva lineárisan független vektorok síkjában fekvő P, az úgynevezett alapján a P sík, ha a vektor síkjában fekvő P felírható.
Opr3.Tri lineárisan független vektorok alapján hívják az űrben, ha a vektor felírható
1. Egy nem nulla vektor, alapját képezi a vonal L.
2. Minden pár noncollinear vektorok síkjában fekvő P alapját képezi a P sík
3. Minden triplett nekomplanaryh vektorok alapját képezi a teret.
(2) a síkban
(3) a térben
Opr4 jobb oldalán (1) képletű, (2) és (3) nevezzük dekompozíciós vektorok a bázisok; ; illetve a megfelelő koordinátákat.
Teorema1: Expansion alapján csak (egyedül!)
Tétel 2 .: A hozzátéve vektorok a megfelelő koordinátákat adunk hozzá. Amikor egy vektorát megszorozzuk számos koordinátáit számának szorzatával
18. A vetítés a vektor a tengelyen. Derékszögű koordináta rendszerben. Iránykoszinuszokat.
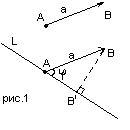
Opr1: Vector vektornak nevezzük vetülete a vektor a tengelyen L.
Opr2: skalár vetülete a vektor a tengelyen L érték:
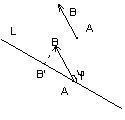
Így erősít Tekintsük a hármas i, j, k (i ^ j) = (i ^ k) = (j ^ k) =; | i | = | j | = | k | = 1 ;. O pont - az általános kiindulási pont. Vektor i határozza meg az x tengely, J - Oy tengelyen, k- Oz tengely.
Így, már bevezetett egy Descartes-féle koordináta-rendszer prostranstve.Pust t m. - tetszőleges pont. Mi befejezni a téglatest átlós OM.
A hossza a bordák | x |, | y |, | z |. Koordináták TM - valós számok x, y, z;
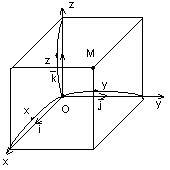
Nyilatkozat: A derékszögű koordinátái pontok egybeesnek belső nyúlványok a vektor a megfelelő tengelyek:
- téglalap alakú; y = OA = | | Cos = | | Cos =
Hasonlóképpen, az X és Z.
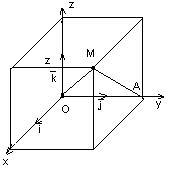
Definíció: Az értékek az úgynevezett iránykoszinuszokat a vektor.
Elosztjuk mindkét fél által
19. A dot terméke két vektor és annak tulajdonságait.
Opredelnie: Az érték (a, b) = | a | * | b | * cos (a ^ b) az úgynevezett belső Avenue enni a és b vektorok. Nyilvánvaló, hogy tud írni (a, b) = | a | * (vetítés ab) és fordítva.
A tulajdonságok a skalár termék:
4) (a, a) ≥0, ahol (a, a) = 0, ha a = 0.
(A, b + c) = | a | * (vetítési (b + c), hogy a) = | a | * (a vetülete B A) + | a | * (a vetülete C-on) = (a, b) + (a, c) .Skalyarnoe terméket egyenlő 0, ha, és csak akkor, ha egy merőleges b, vagy a = 0 vagy b = 0.
20. A vektor terméket és annak tulajdonságait. Szükséges és elégséges feltételei egy egyenesbe esik vektorok.
Opredelnie: A c vektor az úgynevezett vektor termék a és b, jele c = [a, b], ha | C | = | a | * | b | * sin (a ^ b), c merőleges A és B, ABC- jobbra tripla.
Tulajdonságok vektor termék:
Lemma a = b ó bármely d (a, d) = (b, d)
- A végén a munka -
Ez a témakör tartozik a fórumban:
Definíció mátrix Egy dimenziója Sxn nevezett téglalap alakú asztal számok álló S sorból és n oszlopból. elem a mátrix.