Összehasonlítása készletek 1
6. § összehasonlítása készletek. Számlálás a több. 62
6.1. A koncepció a teljesítmény beállítása 62
6.2. A számláló 64 szett
6.3. Uncountability több 67
A koncepció a áramfejlesztőt
Az alapító a tanítás a csomag egy Georg Cantor német matematikus (G. Kantor, 1845-1918), egyetemi tanár a Halle. Az egyik nagy érdemei Cantor, hogy megalapította a pontos fogalmak felmerülő probléma végtelen halmazok sraveneniya legnagyobb és térfogat. Ez a probléma triviális véges készletek és oldotta meg, hogy összehasonlítjuk a tételek számát bennük. De végtelen halmazok a feladatot összehasonlítjuk a kapott eredményeket egy nehéz probléma: végtelen számú eleme egy sor, hogy fontolja meg nagyobb, egyenlő vagy kisebb, mint végtelen számú eleme egy másik? A Motion Cantor, egy összehasonlítást végzünk a két kölcsönösen-egy megfeleltetés közötti elemek.
Azt mondják, hogy az elemek a két

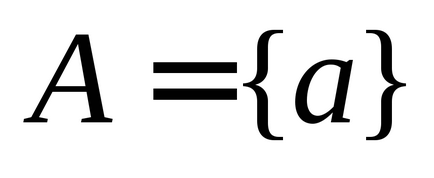
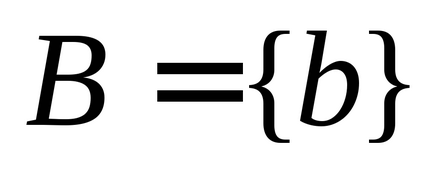
1) minden egyes eleme
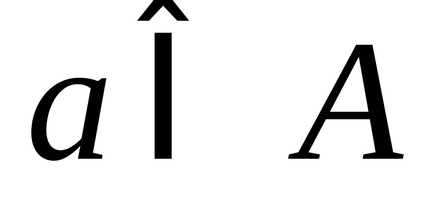
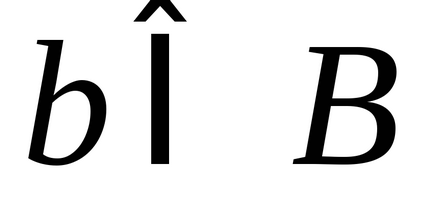
2) elemek mindegyike
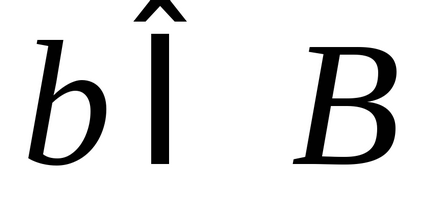
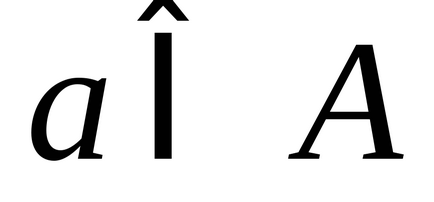
Meghatározása ekvivalens (ekvipotenciális) készletek
Két, elemei között, amely képes létrehozni egy az egyhez megfelelés (bijekciót) nevezik egyenértékű a készlet. vagy beállítja az azonos számosságú. vagy azzal egyenértékű a beállított teljesítmény.
Rendeltetése ekvivalens (ekvipotenciális) állítja:
Így az elemek között megegyezik (ekvivalens) meghatározza mindig létezik egy bijektív leképezést. Ha egy ilyen térképet nem lehet beállítani, a készletek különböző teljesítményűek. Kiderült, hogy nem számít, hogy hogyan lehet próbálja összehangolni elemeit mindkét, mindig lesz további elemeket, sőt, mindig ugyanarról a készlet, ezért „több energiát.” Például nyilvánvaló, hogy a két véges halmazok azonos számosságú akkor és csak akkor, ha azok tartalmazzák az azonos számú elemet.
Példa (ekvivalens véges készletek)
ahol
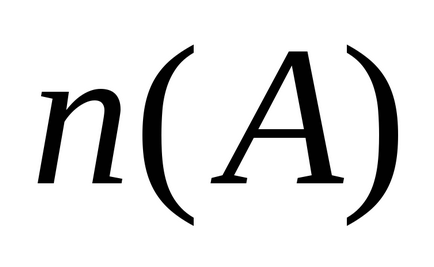
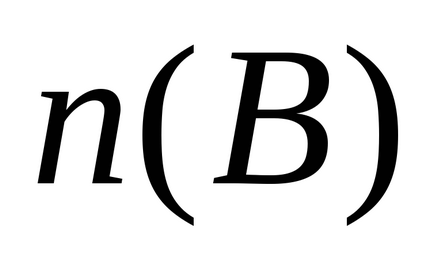

A készlet, amely nem a vége, az úgynevezett végtelen számú elemet és azt nem lehet kifejezni minden számot. Ezért, hogy össze végtelen halmazok csak a saját erő, hogy van egy olyan eljárással, amely meghatározza egy megfeleltetést elemei között ezeket a csomagokat.
Emellett egyértelmű, hogy:
1) a két terminál készlet

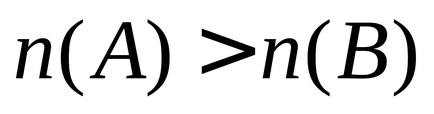

2) Minden véges


Példák (egyenértékű végtelen halmazok)
t. e. mnozhestvoN minden természetes szám azonos kapacitású, mint a saját részét, amely csak páros számok.
2) T. E. Set


készletek

)
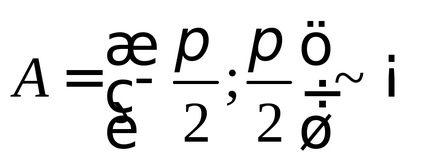
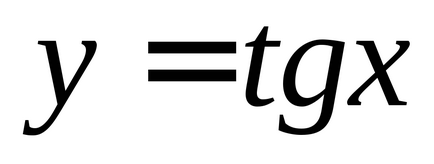
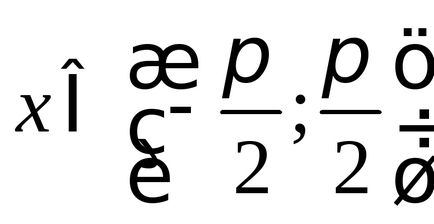
(Ábra. 2), így beállítva
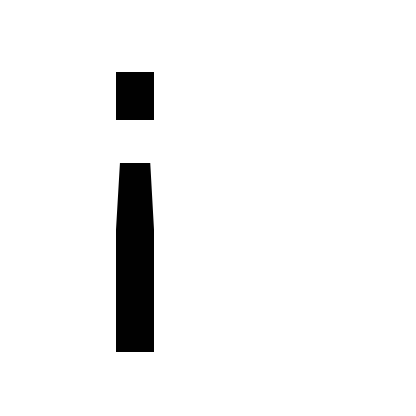
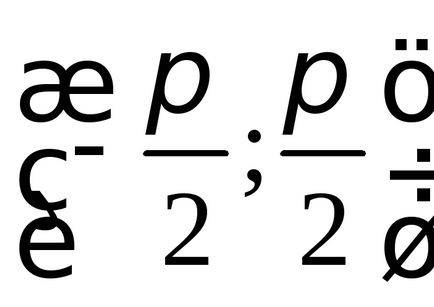
Ezek a példák világosan mutatják, hogy a saját részét a (valódi részhalmaza) egy végtelen halmaz egyenlő erő vele, hogy ahhoz, hogy egy végtelen halmaz nem igaz állítás „része kisebb, mint az egész.”