Kiszámítása területek síkidomok - studopediya
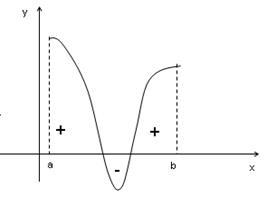
Ismeretes, hogy a határozott integrál egy intervallumot a területet jelöli, egy íves trapéz korlátos ütemezés funkció f (x). Ha a grafikon alatt található tengely Ox, azaz f (x) <0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x)> 0, akkor a terület egy „+” jel.
képletet használjuk, hogy megtalálják a teljes terület.
Példa. Keresse meg a területet az ábra által határolt
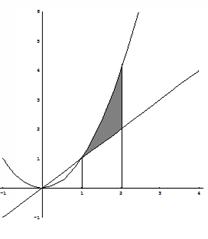
Adottságú terület (satírozott az ábrán) megtalálható a következő képlettel:
Ha görbe trapéz határolt paraméteres görbe
. egyenes x = a, X = B és X-tengely, a területen ez a képlet
ahol # 945; és # 946; meghatározzuk az egyenletek x (# 945) = a és x (# 946;) = b.
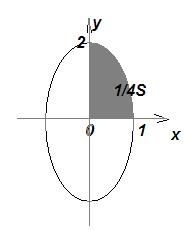
Példa. Számítsuk ki a terület az ábra által határolt ellipszis x = Költség, y = 2sint.
Először találni ¼ négyzet S. Itt, x változik 0-1, t következésképpen megváltoztatja a π / 2 0. Azt találjuk:
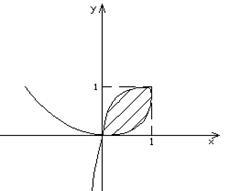
Példa. Keresse meg a területet az ábra által határolt adott paraméteres görbét.
Engedje meg, hogy milyen állapotban határértékek beállított görbe. A funkciók X = x (t) és y = y (t) vannak definiálva, folyamatos és differenciálható bármely aktuális paraméter értékét. Ha. akkor. és ha. . akkor.
A legmagasabb érték x vesz, amikor x „(t) = 0, 2-2t = 0; t = 1, X (1) = 1; y (1) = 1. Ha X = 0, t = 2 és t = 0. Ha ugyanazokat az értékeket a y = 0. Tehát, az a pont koordinátái (0, 0) az a pont az ön-kereszteződések. Ezért, a kívánt terület korlátozott hurok görbe található meg egy első negyedben, és megfelel egy variációs paraméterek a t = 0 és t = 2 a pozitív bejárás irányba.
A területet a kívánt alakú lehet kiszámítani a következő képlettel
Mivel egyes görbék által meghatározott egyszerű paraméteres egyenleteket, a számítás a terület az ábra által határolt zárt görbe derékszögű koordináta gyakran könnyebb elvégezni, majd a paraméteres formában az írás.