Basics scilab
Fontos kifejezések
Scilab (értsd Sayleb) - A csomag az alkalmazott matematikai szoftver, egy hatalmas nyitott környezet mérnöki (műszaki) és a tudományos számítástechnika.
CeCILL (az «CEA CNRS INRIA Logiciel Libre») - engedéllyel szabad szoftver, alkalmazkodik az internacionalista törvény és a francia jog ilyen GNU General Public License, és megőrzi ezek kompatibilitását.
A rendszer m lineáris egyenletek n ismeretlennel (vagy lineáris rendszert, továbbá használt rövidítést SLAE) a lineáris algebra - egy olyan rendszer egyenletek formájában
Közönséges differenciálegyenletek (ODE) - differenciális egyenlet formájában
ahol - ismeretlen funkció (esetleg vektor-értékű függvény, akkor a szabály, továbbá egy vektor értékű függvény, melynek értékei a tér azonos méretű, ebben az esetben beszélhetünk differenciálegyenlet-rendszert), ami függ a független változó, az elsődleges jelentése differenciálódás tekintetében. A szám (a sorrendben a legmagasabb-származék, része az egyenletnek) nevezzük a sorrendben a differenciálegyenletek (1)
1. Számítógép Matematika rendszer Scilab: történelmi fejlődés. Képességek és legfontosabb jellemzőit. Előnyök és hátrányok.
Scilab több száz matematikai függvényt, és képesek arra, hogy új, írott különböző nyelveken (C, C ++, Fortran, és így tovább. D.). Vannak még különböző adatszerkezeteket (listák, polinomok, racionális függvények, lineáris rendszerek), egy tolmács és egy magas szintű nyelven.
Scilab úgy lett kialakítva, mint egy nyitott rendszer, és a felhasználók kiegészítését a típusok és műveletek túlterhelése.
különféle eszközök állnak rendelkezésre a rendszerben:
2D és 3D grafika, animáció
Lineáris algebra, ritka mátrixok (ritka mátrixok)
Polinom és racionális függvények
Interpoláció és közelítése
Szimulációs: ODE oldat és a kontroll
Scicos: hibrid dinamikus rendszerek modellezése és szimulációs rendszer
Differenciál és differenciális optimalizálása
jelfeldolgozás
párhuzamos működés
statisztika
Munka számítógéppel algebra
Interfész a Fortran, a Tcl / Tk, C, C ++, Java, LabVIEW
Scilab hasonló a MATLAB programozási nyelv. A csomag tartalmaz egy segédprogram, amely lehetővé teszi, hogy megtérít dokumentumok Matlab Scilab.
Scilab munkavégzést biztosít az általános és számos speciális funkciók (Bessel, Neumann, beépített függvény) hatásos eszközöket dolgozni mátrixok, polinomok (beleértve a szimbolikus) előállításához numerikus számítás (például numerikus integráció) és a problémák megoldását lineáris algebra optimalizálása és szimuláció, erős statisztikai funkciók, valamint egy eszközt építeni, és dolgozni diagramok.
A numerikus számítások LAPACK könyvtár, LINPACK, ODEPACK, Atlas és mások.
A csomag tartalmaz Scicos - szerszám szerkesztésre Blokkdiagramok és szimuláció (analóg Simulink csomag MATLAB). Scilab lehet dolgozni a LabVIEW programmal.
Főbb jellemzők
Ellentétben egyes kereskedelmi programok:
Ingyenes.
Free (5.0 verziótól).
Kis méretű művek - 4-es verzió kevesebb mint 20 MB ellen kettőnél több gigabyte-os csomag MATLAB. 5. A telepítő verzió (5.4.0) mennyiségének növekedése, akár 108 MB.
Képes futtatni a konzolon használata nélkül a grafikus felület, beleértve a verziót a Windows (UNIX és Windows változatait MatLab de ez a funkció elérhető is). Ez lehetővé teszi az automatikus számítás, van egy kötegelt módban.
Előnyök és hátrányok
A keresés előnyei és hátrányai az interneten, hogy nem ad. Szóval beszélni, hogy mit láttam magam.
Ha beszélünk az érdemi, ott van a legalapvetőbb nekem is szabad ezt a csomagot, mint az azonos Matematika, mikor kell elvégezni a laboratóriumi munka kellett találni a sorozatszámot vagy repedés. Következő - egy cross-platform, mert Inkább a Gentoo, mint a Windows. Alapvetően a legtöbb előnyt bekezdésben leírt legfontosabb jellemzői.
Közül a hiányosságokat látok, csak 2: Ez nem egy vizualizációs szoftver matematikai, valamint a rendszer elsősorban numerikus számítási módszereit, amelyek befolyásolhatják a pontosságot.
2. alapjai Scilab. Felhasználói és rendszer változókat. Matematikai kifejezések. megjegyzések
Mielőtt tovább, nézzük a felület is. Amikor futtatja a parancsot ablak.
2 lehetőség dolgozni: 1 - ez a munka azonos parancs ablakban 2 - nyitott SciNotes (olyasmi, mint egy notebook háttérvilágítás), ahol ez lehetséges, hogy írjon kódot, amelyet később fut, a végrehajtás fog eredményezni parancsablakban.
Például úgy vélem, az eredmények Hellow világon.
Command Prompt. Az O funkció disp () megjelenítése

Amikor dolgozik SciNotes kapsz valami hasonlót
futtatni a kódot, akkor vagy kattintson a nyílra :) (mint sok fejlesztési környezetben)
vagy Vypolnenie-> ... anélkül, hogy a kijelző a parancsok
és egyéb végrehajtási módszereket lehet használni, elvileg, és ne használja kimenetét a képernyőre
teljesítmény lesz az eredmény:
mert azt mondhatjuk, hogy a felület tanult, majd adok egy egyszerű kódot, és az eredmény a
Scilab érzékeny a nyilvántartásban, vagyis Az A és a - különböző változók változók.
Alapvető műveletek:
+ kiegészítés
- kivonás
* szorzás
/ Jobb részlege, azaz x / y = xy ^ (- 1)
a szétválás a bal oldalon, hogy van, xy = x ^ (- 1) y
^ Hatványozás, azaz x ^ y
** hatványozási (^ ekvivalens)
„Hermitikus konjugátum (komplex konjugált transzponáltat)
Elemi matematikai függvényeket.
acos acosd acosh acoshm acosm ACOT acotd acoth
acsc acscd acsch ASEC asecd asech asin asind
asinh asinhm asinm atan atand atanh atanhm atanm
cos cosd cosh coshm koz cotd cotg coth
cothm CSC cscd CSCH sec secd SECH sin
sinc sind sinh sinhm sinm tan tand tanh
tanhm tanm
exp expm log log10 log1p log2 logm max
maxi min mini modulo pmodulo jel signm sqrt
sqrtm
y = int8 (x) 8-bites egész szám megjelölés [-2 ^ 7; (2 ^ 7) -1] = [-128; 127]
y = Uint8 (x) 8-bites előjel nélküli egész szám [0; (2 ^ 8) -1] = [0; 255]
y = int16 (x) 16-bites egész szám megjelölés [-2 ^ 15; (2 ^ 15) -1] = [-32768; 32767]
y = uint16 (x) 16-bites előjel nélküli egész szám [0; (2 ^ 16) -1] = [0; 65535]
y = int32 (x) 32-bites egész szám megjelölés [-2 ^ 31; (2 ^ 31) -1] = [-2147483648; 2147483647]
y = uint32 (x) 32-bites előjel nélküli egész szám [0; (2 ^ 32) -1] = [0; 4294967295]
iconvert átalakítás egy egész ábrázolás
inttype típusdefiníció egész szám
A legegyszerűbb módja annak, hogy hívja az egyéni funkciók:
outvar = myFunction (Invar)
szögletes zárójelben „[” és „]” jelzi a kezdetét és végét transzfer
a mátrix elemei,
vessző „” elválasztva a mátrix elemek ugyanabban a sorban,
pontosvesszővel „;” elválasztja a sorok a mátrix.
méretének meghatározására a mátrix mérete
mátrix változtatni a méret a mátrix
resize_matrix hozzon létre egy új tömböt egy bizonyos méretet, és másolja
benne elemei egy kezdeti mátrix
Műveletek mátrixok:
Fellebbezést a mátrix elemeinek
i = 1; 2 és J = 3; 4
Ehhez, hogy egy kész mátrix
--> A = testmatrix ( "Hilb", 5)
A =
25-300 1050-1400 630.
- 300 4800 - 18900. 26880. - 12600.
1050 - 18900. 79380. - 56700 117600 ..
- 26880. 1400 - 117600. 179200. - 88200.
630 - 12600. 56700. - 88200. 44100.
--> A (1: 2, 3: 4)
ans =
1050-1400.
- 18900. 26880
A mátrix teljes egészében
A (.) Az egész mátrix
A (i: j, k) a mátrix elemei a k-edik oszlopának az i-edik a j-edik sorban
A (i, j: k) a mátrix elemei az i-edik összhangban a j-edik, hogy k-edik oszlop
A (i, :) i-edik sorának a mátrix
A (:, j) j-edik oszlopa a mátrix
Generáló egységet mátrix
manipulálása mátrixok
+ Amellett. + robbantott kívül
- kivonás .- felrobbant kivonás
* Szorzás. * Element-bölcs szorzás
/ Jobb osztály ./ jobb osztály robbantott
a szétválás, a bal oldalon. elemenként felosztása a bal
* Vagy * hatványozási ^ felrobbant hatványozást
„Hermitikus konjugátum (komplex konjugált transzponáltat)
.„Anélkül, konjugáció transzponálás
Példa edenichnye megszorozzuk egy számot 2 mátrix 2
5. meghatározása dimenziós, többdimenziós tömböket. Különleges mátrix függvények
funkciók működnek mátrixok
kol Cholesky bomlás
társ társ mátrix
vez állapotban száma
det meghatározója a mátrix
a fordított mátrixba inv
linsolve megoldására rendszerek lineáris egyenletek
lsq legkisebb négyzetek módszere
Lu Lu-bomlás a választás a tartóelem
QR QR-bomlás
rcond inverz állapotban száma
spec sajátértékek és vektorok
SVD egyenkénti érték felbontását a mátrix
testmatrix generációs speciális mátrixok (Hilbert, Franck et al.)
nyoma nyoma a mátrix
6. meghatározása dimenziós, többdimenziós tömböket. Megoldás Slough. Karakter tömbök és műveletek rájuk
Szöveg script fájlt a probléma megoldása a Cramer-szabály
--> A = [1 2 1 -5, 1 0 -3 -6, 0 2 -1 2, 1 April -7 6]; // Matrix együtthatók
--> B = [8, 9, -5, 0]; // free vektor együtthatók
--> // első kiegészítőréteg tömb
--> A1 = A; A1 (:, 1) = b;
--> // második kisegítő mátrix
--> A2 = A; A2 (:, 2) = b;
--> // harmadik kiegészítő mátrix
--> A3 = A; A3 (:, 3) = b;
--> // A negyedik kiegészítő mátrix
--> A4 = A; A4 (:, 4) = b;
--> // A fő meghatározója nem zérus
--> D = det (A);
--> // kisegítő mátrixok és determinánsok
--> D (1) = det (A1);
--> D (2) = det (A2);
--> D (3) = det (A3);
--> D (4) = det (A4);
--> // A vektor az ismeretlenek
--> X = d / D
X =
3.
- 4.
- 1.
1.
--> // megtekintése
--> P = A * x-b
P =
0.
0.
- 8.882D-16
2.665D-15
Megoldás a rendszer által Gauss
--> A = [-1 1 2 3 2 -5, March 1 -2];
--> B = [0; 1; 4];
--> // Így a kibővített mátrix háromszög alakú
--> C = rref ([A b]);
--> // kiosztása az utolsó oszlop a mátrix,
--> // x - rendszer megoldás
--> X = C (1: 3.4: 4)
X =
0.4642857
1.6785714
0.75
--> A * x // megtekintése
ans =
- 5.551D-16
1.
4.
7. Numerikus integrálás. Megközelítései integráció. Integrálása a felhasználó által definiált függvények
Numerikus integrálás (történelmi neve: (numerikus) Terület) - értékének kiszámítása a határozott integrál (általában körülbelül). Numerikus integrálással megérthető meghatározott numerikus módszerek megtalálására az érték a határozott integrál.
Integráció tekintetében a trapezoid módszer
integrálja funkció, a gyökér a 2 * X-1 intervallumban 1-től 10 a partíció a 1. lépésben
--> X = 1: 10
X =
1. 2. 3. 4. 5. 6. 7. 8. 9. 10..
--> Y = sqrt (2 * x-1)
y =
oszlop 1-től 6
1. 1,7320508 2,236068 2,6457513 3. 3,3166248
oszlop 7-10
3.6055513 3.8729833 4.1231056 4.3588989
--> Inttrap (x, y)
ans =
27.211585
Quadrature képletű Newton Cotes
8.Chislennoe differenciálás. Megközelítései differenciálás.
Numerikus differenciálás - egy sor számítási módszereit diszkrét értékeket a származék adott funkció.
A származtatás alapjául a numerikus közelítés a funkciót, amellyel a származék kerül sor, az interpolációs polinom. Az összes alapvető képletek numerikus differenciálás lehet előállítani, hogy először Newton interpolációs polinom (Newton képlet az elején a táblázatban).
a
v = 0: 3;
--> Numdiff (én, v)
ans =
17. 0. 0. 0.
0. 32. 0 0.
0. 0. 0 52,999999.
0. 0. 0. 80,000002
--> Funkció f1 = my1 (x), F1 = 3 * (x + 2) ^ 2 + 5, endfunction;
--> My1 (v)
ans =
17. 32. 53. 80.
9. TAC döntés azt jelenti, Scilab. Funkció használható, hogy megoldja a ODE. Megoldása határ érték problémák.
4 számos mód van, hogy megoldja a ODE:
1. A rendszer segítségével a óda csapat, amely végzendő megoldás a rendes
differenciálegyenlet.
2. odedc csapat, amely kiszámítja egy vegyes megoldás diszkréten
folyamatos rendszerben.
3. dassl parancs ami a megoldás a differenciálegyenlet kifejezett hallgatólagosan.
4. impl parancs, ami a megoldás hallgatólagosan kifejezett lineáris
differenciálegyenlet.
--> Y0 = 1;
--> T0 = 1;
--> T = 1: 0,01: 1,5;
--> Deff ( "[ydot] = f (t, y)", «ydot = y ^ (1/3) * t»)
--> Y = ODE (y0, t0, t, f);
--> Y_exact = ((t ^ 2 + 2) / 3) ^ (1.5); // ez a funkció a pontos megoldást az összehasonlítás
--> My_er = y-y_exact;
--> Plot (t, y-y_exact) // grafikon számítási hiba a argumentum t
Az eredmény egy grafikon
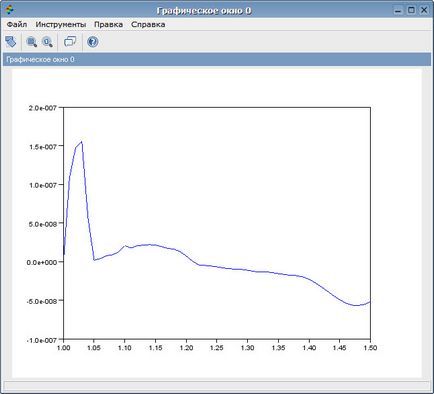
egy látható a grafikus ablakban. Felrajzolása kerül az alábbiakban részletesen ismertetjük.
10. Építőipari kétdimenziós ábrákat Scilab rendszerben. A fő funkciók és típusú diagramok.
függvény telek
Vegyük ezt a példát:
mint látható az első paraméter a függvény - egy szegmens, a második funkció
mert lehetséges, hogy dolgozzon több funkció, megnevezni őket: