Példák a potenciális mezők
1. Tekintsük a tömegpont gravitációs mező m, van elhelyezve a származási O (0,0,0). Ez a mező le egy vektor funkció. ahol # 947; - gravitációs állandó - sugara vektor egy pont. . Egy ilyen erőtér ható darabsúlya kerül egy pontot. A gravitációs mező lehetséges. Ez is képviselteti magát a gradiens skalár függvény. úgynevezett newtoni potenciális tömegpont gravitációs mezőben m. Tény:
2. mező az elektromos töltés e pont, van elhelyezve a származási pont leírt vektor a feszültség. (..) Ez a mező lehetséges. Ez is képviselteti magát a gradiens skalár függvény. amely elektromos mező az úgynevezett potenciális ponttöltés e ..
8. meghatározása sík felületen (szintvonal egy sík területen) potenciális nevezzük ekvipotenciális felületek (vonalak).
Megjegyezzük, hogy a ekvipotenciális felületet (vonal) és a vonal vektor, áthalad egy közös pont. merőleges rá.
13. példa Teszt e területen lehetséges. Ha igen, akkor megtalálják a potenciális a területen, épít potenciális vonalak és vektoros mező vonalon. Válassza vektor és ekvipotenciális vonalak ponton áthaladó.
Határozat. Mező határozza meg a teljes síkon XOY.
Ellenőrizze, hogy a szükséges és elégséges feltételeit lehetségesség teljesül :. mező lehetséges.
1. Ahhoz, hogy megtalálja a funkció egy olyan rendszer felállítása :.
Az első egyenlet integrálásával, hogy az x változó. találni:
.(A szerepet játszik itt egy állandó, minden funkció függően x). Ahhoz, hogy megtalálja behelyettesítve a függvény a második egyenletet:
2.Uslovie ekvipotenciálisaknak. . megkapjuk a család ekvipotenciális vonalak.
Adunk az egyenlet kanonikus formában:
Ez a családi túlzás, mikor.
Ha. Megkapjuk az egyenletek a vonalak.
Építünk egy potenciális vonalak a gépen XOY.
3.Vektornye sorközzel. Alkotunk differenciálegyenlet vektor vonalak területén: .Reshim azt.
- családi túlzás, ha. és két egyenes. if. Épület egy vektor vonal a gépen XOY.
Ekvipotenciális és vektor vonalak merőlegesek a metszéspontot. Ellenőrizze, hogy ki a sorokat ponton áthaladó.
4.Podstavim pont koordinátáit az egyenletben a vektor vonalak :. M átmegy a ponton vektor vonalat.
Analóg módon, hogy megtalálják ekvipotenciális vonal ponton áthaladó M. Ez áthalad az M pont ekvipotenciális vonalat.
Kiszámoljuk a lejtőn a Érintőa görbe M pont:
A vektor vonal: M t.:.
Az ekvipotenciális vonalak a M r.:.
- a feltétele a két merőleges érintők.
Következtetés: vektor és potenciális vonalak M ortogonális.
14. példa arról, hogy a mező egy potenciális, megtalálni a potenciális területen, és kiszámítja a munkát, amelyet ezen a területen, ha mozog egy anyagi pont.
Határozat. A kérdés megválaszolásához a lehetséges ezen a területen kell számítania parciális deriváltjai funkciókat. . . Ezek a funkciók folyamatos együtt annak részleges származékai bármely pontján.
Látjuk, hogy az alábbi szükséges és elégséges feltételei a potenciális területen. . . . h. t. d.
Kiszámítani a lehetséges felhasználása a tényt, hogy a vonal integráns adott mezőben nem függ az integráció útján, és ki lehet számítani a képlet alaptételének. Hagyja, hogy a pont - az elején a pálya, de néhány ponton - az út vége. Kiszámítjuk az integrál egy kontúrja mentén, amely egyenes vonal szegmensek párhuzamosak a koordináta tengelyek (lásd 10. ábra). .
Az egyenletek az áramkör részek :. . .
. x értéke rögzített, ezért,
. Itt ez fix y. így van.
Ennek eredményeképpen megkapjuk :.
Most, az azonos szerves által kiszámított Newton-Leibniz formula. =.
Ebből az egyenletből következik, hogy. és a lehetséges ezen a területen található.
Találunk a munkát, amelyet a vektor mező mozgás közben egy ponton. A lehetséges munka területén egyenlő a potenciális különbség a kezdeti és a végső pont az út, azaz a. E.
15. példa Annak biztosítása potencialitást vektor mezőben. megtalálni az egyenleteket ekvipotenciális felületek, és válassza ki közülük azt, amelyik átmegy az M pont (2.1.1).
Határozat. Mező határozza meg minden pontján a teret. Ellenőrizze potenciális mezőben (lásd (11)).
feltételek teljesülnek, a mező a potenciál. Megtalálható potenciál, ugyanúgy, mint a 12. példa, de lehet bármilyen más módon. Ahhoz, hogy megtalálja a rendszer kapacitását, van:
Integrálása az első egyenletben, hogy x a rendszer. találni. Mi különbözteti meg a kapott kifejezést y: .A második egyenletet kapjuk: .Utochnim kifejezés a potenciál:
. Differenciálható tekintetében z és hasonlítsuk össze egy harmadik egyenlet rendszer :.
Összes visszaállítása funkció :. A potenciális megtalálható.
Igényes. Kapjuk egyenletek ekvipotenciális felületek:
Adunk ez az egyenlet a kanonikus formában.
Ez az egyenlet gömbök középpontú O pont (0, 1, 1), és a sugara
Találunk egy ekvipotenciális felületet ponton áthaladó M (2.1.1). Behelyettesítve a koordinátákat a felület egyenlete, mi határozza meg:
Ez áthalad az M pont szolgáltatásokat.
Találunk egy vektor erővonalán átnyúlik a lényeg M.
Az egyenletek vektor sorokat:
M t: ...., azaz áthalad t M vonalon. mert áthalad a központja a gömb, az érintő sík a gömb t. M arra merőleges. E. A vektor vonal és a ekvipotenciális felületet a m. M kölcsönösen ortogonálisak.
A mozgási irányának területén e vonal mentén egybeesik a tengely irányában OX x> 0, és vele szemben az x<0. Это совпадает с направлением увеличения потенциала U. Действительно, чем больше потенциал, тем больше радиус сферы.
Ellenőrző feladat 6.
1. Ellenőrizze, hogy a vektor mező lehetséges. Megtalálja a lehetőségeket. Ábrázolják vonalak egyenlő lehetőségeket. Keresse meg a vektor vonalak és képviselje őket az ábra mutatja. Számolja terepmunka anyag mozgás közben pontról pontra. Keresse meg a vektor vonal és ekvipotenciális vonal áthalad a ponton.
2. Ellenőrizze, hogy a vektor potenciál területén. Ha igen, akkor megtalálja a potenciál.
3. Keresse meg a lehetséges a gravitációs mező.
4. Mutassuk meg, hogy a vektor mező potenciálja és megtalálja bennük rejlő lehetőségeket.
Áramlási vektor mezőben.
enged # 963; - néhány orientált felület G. döntünk bizonyos mellé, amelyben az egység vektor felületre merőleges.
9. meghatározása a fluxus vektor a felületen keresztül # 963; Ez az úgynevezett felületi integrálja a skalár szorzata a vektor mezőben a normál egység vektor: P. (13)
Vannak más vektor stream felvételt. Például, mivel megkapjuk Pr: P.
Vagy megadható egy vektor. mentén irányul felületre merőleges, oly módon, hogy :. . Aztán :. (14)
Ha a felület # 963; zárt, általában egy vektor irányba tett irányára merőlegesen a külső felület és jelentésük
Ha megváltoztatja a tájolás (hogy a másik oldalon a felület), skalár szorzata, és ennek megfelelően az áramlás változása jel.
Az adatfolyam felírható komponens formájában, bemutatva a megfelelő skaláris szorzata vektorok:
ahol a jobb oldalon van a felületi integrál a második fajta.
Mind a kifejezések általános képletű (17) alakítunk át egy kettős integrál a régió, amely egy vetítési felület D. # 963; a megfelelő koordinátarendszerben:
ahol - vetítés # 963; Oyz a koordinátarendszerben, Oxz, Oxy volt. A jel előtt egy kettős integrál a jobb oldalon egybeesik a jel a koszinusza közötti szög a felület normál vektor és a pozitív irány a tengelyek Ox, Oy, Oz, ill. A kifejezések kapott kifejező változók a felület egyenlete # 963;:. Lehetőség van, hogy csökkentse a számítás áramlási számítására az integrál az első fajta, helyettesítő (16) képletű. . .
16. példa kiszámíthatja az áramlási vektor mező egy részén át, a sík. zárt az első oktáns, abba az irányba, a normális összetevője a tompaszög a OY tengellyel.
A (13) képletű. ahol # 963; - S sík :.
Emlékezzünk vissza, hogy a normál vektor síkjára egyenletnek formájában. A mi a probléma. Ez a vektor hegyesszöget alkot a OY tengellyel. Aztán.
Csökkentjük a probléma, hogy a számítás a szerves valahogy (lásd (13).).
De. azaz . Vektor algebra ismert, hogy a háromszög területe MNP (lásd 12. ábra) A :.
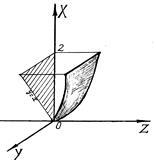
Megtalálni a fluxus vektor mező egy részén át, a felület. ha a vektor merőleges a felületre hegyesszöget alkot a pozitív tengely irányában OX.
Határozat. Mi képezik szerves kiszámításához az áramlási mező:
A 12. ábrán azt látjuk, hogy a vektor teszi az OX hegyesszöget OY - összhangban OZ - obtuse ezért.
Kiszámítható. A vetítés a kereszteződésekben a vonal és sík Yoz :. Aztán: .A egyenlet felületre. majd
Kiszámítható. A felület egyenlete. majd
Az eredmény lehet ellenőrizni csökkenti a problémát, hogy a felületi integrál I. típusú Ehhez találni és ki kell számítani a iránykoszinuszokat. Ha a felület az egyenlet. a normál vektor. a.
A példában (15), a felület egyenlete :. Tekintettel arra, hogy a normál vektor hegyesszöget alkot a tengellyel OX. Van. Aztán.
Ennek számításához szerves tervezek egy ilyen # 963; a XOY síkban (lásd. 12.), akkor:
A felület egyenlete. . .
Ellenőrző feladat 7.
1. Find fluxus-vektor mező egy részén át, paraboloid két módon, képletek szerint (15) és (17).
2. Számítsuk ki az áramlási vektor mező keresztül orientált felületi # 963;, ha: a) # 963; - része egy kúp alakú felület. normál külső; b) # 963; - része a gépet. .
3. Számítsuk ki áramlási vektor mező egy részén át egy gömb.