Numerikus jellemzőinek véletlenszerű folyamatok, az alapvető tulajdonságait a korrelációs függvény - véletlenszerű
Elvárás (átlagos érték) a sztochasztikus folyamat X (t) az úgynevezett nem-random idő függvényében MX (t), amelynek értéke minden időpontban megegyezik a középértéke a megfelelő véletlenszerű folyamat részben
Így mx (t) jelenti a szimmetriatengelye, mint ha az egyes megvalósítások, t. E. diszperziós fok tekintetében a középtengellyel.
A stacionárius folyamatok
Mert ergodikus folyamatok
Az átlagos sztochasztikus folyamat X (t) jelzi az átlagos négyzetes folyamat kimeneti és adja meg:
A stacionárius folyamatok
Mert ergodikus folyamatok
Diszperziós sztochasztikus folyamat X (t) az úgynevezett nem-random idő függvényében Dx (t), amelynek értéke minden időpontban megegyezik a diszperziót a megfelelő szakasz a véletlen folyamat
A stacionárius folyamatok
Mert ergodikus folyamatok
Várható értéke és szórása jellemzi a folyamatot külön részben, de nem veszik figyelembe a kapcsolatukat, ez a kapcsolat jellemzi a korrelációs függvény.
Korreláció (autokorrelációs) véletlenszerű funkció X (t) a folyamatot nevezzük a két nem-random funkciót Rxx (t1, t2) az érv, amely minden egyes pár értékek T1 és T2 jelentése azonos érvek korrelációs idő megfelelő szakaszokra véletlen folyamat
A korrelációs függvény jellemzi statisztikai kapcsolat a két rész közötti véletlenszerű folyamat.
Kereszt-korrelációs függvény egyenlő
Kereszt-korrelációs függvény jellemzi statisztikai összefüggés a keresztmetszet a két folyamat.
A Gauscovskih véletlenszerű folyamat meghatározó jellemzője kétdimenziós valószínűségi sűrűsége, így a korrelációs függvény teljes mértékben jellemezni statisztikai tulajdonságait a véletlen folyamat.
A stacionárius folyamatok a korrelációs funkció függ a különbség a érvek = t2 -T1
Ebben az esetben a szórás
Mert ergodikus folyamatok
A fő tulajdonságai a korrelációs függvény
1. A kezdeti értéke a korrelációs függvény egyenlő a diszperziós
2. Az értéket Rx () minden egyes nem haladhatja meg a kezdeti érték
3. A korrelációs függvény szimmetrikus érveit
A kereszt-korrelációs függvény nem igazságos
4. A korrelációs függvénye stacionárius folyamatok egy még funkciója és kereszt-korrelációs - páratlan
5. Összefüggés összege z (t) = X (t) + Y (t), ahol X (t) és y (t) - véletlenszerű folyamatok
6. A korrelációs függvénye a termék Z (t) = X (t) Y (t), ahol X (t) egy véletlenszerű folyamat, és Y (t) -, nem véletlenszerű akadálytalanul
7. A korrelációs függvénye összeg Z (t) = X (t) + Y (t), ahol X (t) - véletlenszerű folyamat, és Y (t) - véletlenszerű funkció
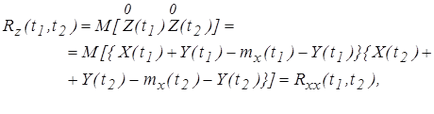
8. autokorrelációs függvény felírható kifejezést
A kereszt-korrelációs funkció írásbeli kifejezés