lu-faktorizáció módszerrel
Az LU-faktorizáció módszer (ez a rendszer az úgynevezett Gauss kompakt rendszer) oldatot a rendszer, a következő műveletsorozatot.
A mátrix képviseli, mint a termék
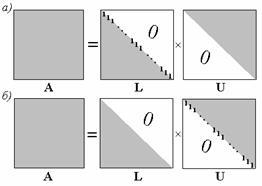
Ábra. 2.3. A szerkezet a mátrixok L és U a bővítések Doolittle (a) és Kraut (b)
ahol L - alsó háromszög mátrix, U - felső háromszög mátrix. Ez bomlás egyedülálló a technika megválasztása egyik átlós elemek a mátrixok. Ebben az esetben, az elemek száma a mátrix egybeesik a teljes száma az ismeretlen elemeit a mátrixok L és U. Ha a készülék megkapta az átlós L, egy ilyen bomlás az úgynevezett bomlás Doolittle (2.3 ábra, a.) Ha a készülék átlós U - bomlás Kraut (2.3 ábra. , b). A jövőben az építési módszer LU- faktorizációs magában bővítése Kraut.
A rendszer helyébe egy olyan rendszer
könnyen megoldható két lépésben:
1. lépés. Figyelembe véve a háromszögmátrix L. könnyen látható, hogy az algoritmus Kraut
2. lépés. A megoldás ebben a rendszerben az algoritmus Kraut:
A teljes költség végrehajtásához mind a lépéseket, amikor n >> 1 a hosszú műveleteket.
Relationships kiszámításához elemei a mátrixok az L és U Kraut algoritmus. Erre a többszörösen mátrixok az L és U és egyenlővé az eredményt A. A szabály mátrix szorzás
Tekintsünk egy elem (ábra. 2.4), amely a középső átlós vagy alacsonyabb háromszög alakú résznek a mátrix A. Az ilyen elementai ≥ j. Az ábrából következik, hogy
Ábra. 2.4. Illusztráció a mátrix számítási alapegységhez elrendezve
alatt a fő átló
mivel i ≥ j és. itt
Tekintsünk egy elem (ábra. 2.5), felett található a fő
Ábra. 2.5. Illusztráció a mátrix számítási alapegységhez elrendezve
fölött a fő átló
diagonális mátrix (számára j> i). Ebben az esetben,
Kaptunk eredményeként arányok, amelyek lehetővé teszik, hogy kiszámítja az elemek a mátrixok L és az U. szekvenciáját számítások: első oszlop a mátrix számítjuk L. U. további sora a mátrixszal, majd a mátrix L. oszlopra ismét további sora a mátrix U, és így tovább (lásd az ábrát 2.6 .... ábrán látható a folyamatábra a számítási és tárolási mátrixok az L és U).
Kiszámítása oszlop a mátrix L és U mátrix vonalat nevezzük lépést LU-bomlás. Itt, mint például a tároló áramköri elemeket a mátrixok A, L, U a második lépés után LU-bomlás (ábra. 2.7).
A szám a hosszú aritmetikai művelet lépésben LU-bomlás már n >> 1 mennyiségben. döntések Li- lépés
Lineáris rendszerek háromszög mátrixok -. A teljes műveletek száma közelítőleg egyenlő hosszú (mint a módszer Gauss)
Ábra. 2.6. A kezdeti mátrix (a), a tároló áramkör L és U mátrixok (b), a szekvencia kiszámítása kapott tároló elemek a rendszerben (c)
Ábra. 2.7 4'4 reakcióvázlat tároló elemek a mátrixok A, L, U a második lépés után LU-faktorizáció
.. Vagyis a főbb költségek esik az LU-faktorizációja A. Ez a funkció teszi a különösen vonzó módja LU-faktorizációs megoldására lineáris rendszerek ugyanazt mátrix, de eltérő jobb oldalán:
Ebben az esetben a mátrix faktorizáció végezzük egyszer, hogy a kívánt hosszú műveletek, és mindegyik rendszer megoldást a megfelelő jobb oldali van megvalósítva az ilyen műveletekre.
Rendkívül hatékony végrehajtásának LU-faktorizációt módszerrel állíthatjuk elő, ha korlátozzuk az osztály Lineáris rendszerek, szimmetrikus pozitív definit mátrix A. t. E. Az ilyen végrehajtás az úgynevezett a Cholesky módszerrel vagy a négyzetgyök.
Feltételezzük, hogy a rendszer megoldható
van egy pozitív definit szimmetrikus mátrix A. Ebben az esetben, az A mátrix képviseletében a
Itt - egy alsó háromszög mátrixot. Az ilyen tágulási létezik és egyedi pozitív definit szimmetrikus mátrixok.
A rendszer átalakul
A vektort keresett sorrendben megoldására két háromszög rendszerek mátrixok:
A kiszámított kapcsolatok mátrix elemeinek tartjuk egy tetszőleges eleme a mátrix:
Az összegzési végezzük csak j. t. Hogy. j≤i. Mi kiválasztjuk tagja értékben k = j:
Ezek a kapcsolatok lehetővé teszik számunkra, hogy meghatározzuk a mátrix oszlopai elemekkel.
A hatékonyságát ez a módszer úgy érjük szakaszában bomlás a mátrix, azaz. K. kiszámításához szükséges ebben az esetben az egyetlen mátrixban. Számtani költségek módszer Cholesky jelentenek hosszú műveletek és extrakciós műveletek n négyzetgyöke.
Van egy másik lehetőség bomlás szimmetrikus pozitív definit mátrix, amely elkerüli kitermelése négyzetgyök műveleteket. Ebben a kiviteli alakban tartalmaz egy új mátrixot a szabály
és - a mátrix korábban által kiszámított Cholesky rendszer, - egy diagonális mátrix mátrix elemeinek. A mátrix létezik, és kisebb, háromszög alakú egységnyi átlós. Ebben az esetben,
A számított arány mátrix elemek és lehet beszerezni, mint korábban, általában magába mátrix szorzás
amiből következik, hogy
t. k. egység diagonális mátrix.
Ilyen algoritmus lenne szükség kétszer annyi, mint szorzásra Cholesky rendszer. Azonban, ha bevezetjük a változás változók
a kiszámított arány fogja képezni
Ott először kiszámítja kiegészítő értékek. majd használja őket, hogy meghatározzuk az ismeretlen mennyiségeket és. A való szorzások ilyen elrendezés algoritmust kb és tartalmaz egy négyzetgyök kivonása működését.