Meghatározása csökkenő függvény
A függvény y = f (x) csökken az intervallum X. Ha bármilyen egyenlőtlenség. Más szóval - a nagyobb érték az érvelés megegyezik a minimális érték a funkciót.
17) A függvény az y = x n. ahol n - egész szám, az úgynevezett exponenciális függvény természetes kitevő. Ha n = 1 megkapjuk a függvény az y = x. Ha n = 2 megkapjuk a függvény az y = x 2 Megjegyezzük, hogy a természetes N erő függvény az egész számegyenesen. A tetszőleges valós n ez nem lehetséges, így a teljesítmény függvényt egy igazi index meghatározása csak a pozitív x. A függvény az y = x 2 listáját a tulajdonságok a függvény az y = x 2 1) a domain a funkció - az egész szám vonalon. 2) y = x 2 - páros függvény (f (- x) = (- x) = 2 x 2 = f (x)). 3) A [0; + ∞) függvény növekszik (ha 0 ≤ x1 <х2. то х1 2 <х2 2. а это и означает возрастание функции). 4) На промежутке ( - ∞ ; 0] функция убывает ( если x1
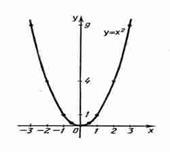
Ha n = 3, megkapjuk a függvény az y = x 3. A függvény az y = x 3 listáját a tulajdonságok a függvény az y = x 3 1) a domain a funkció - az egész számegyenesen. 2) y = x 3 - páratlan függvény (f (- x) = (- x) = 3 - X 3 = - f (x)) 3) A függvény az y = x 3 növeli az egész számegyenesen. A grafikon a függvény az y = x 3 az ábrán látható. Ez az úgynevezett harmadfokú parabola.
17) Az exponenciális függvény, annak tulajdonságait és funkció · grafikon formájában y = a x. ahol a> 0, a ≠ 1, X - bármilyen számú, úgynevezett egy exponenciális függvény. · A tartomány az exponenciális függvény: D (y) = R lehet a készlet minden valós számok. · Az értéktartomány az exponenciális függvény: E (y) = R + - a készlet minden pozitív egész szám. · Exponenciális függvény az y = A x növekszik, amikor a> 1. · Exponenciális függvény az y = A x csökken 0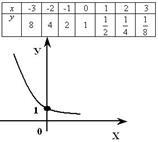
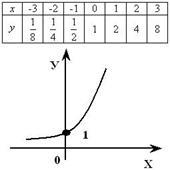
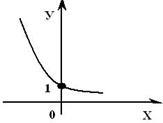
18) A funkció az űrlap y = loga (x), ahol a értéke bármilyen pozitív szám nem egyenlő egységet nevezzük logaritmikus függvény a bázissal a. Itt és az alábbiakban terjeszti a logaritmus is használja a következő jelöléseket: loga (b) - a rekord jelzi a alapú logaritmusa és b.
A főbb jellemzői a logaritmikus függvény:
1. A domain a logaritmikus függvény lesz egy egész sor pozitív valós számok. A rövidség kedvéért, az is kijelölt R +. Nyilvánvaló ingatlan, hiszen minden pozitív szám van alapú logaritmusa.
2. A hatályát értéke a logaritmikus függvény lesz minden valós számok halmaza.
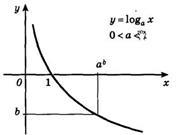
3. Ha az alap a logaritmikus függvény a> 1, akkor a teljes domain a funkció fokozott. Ha az alap a logaritmikus függvény végezzük következő egyenlőtlenség 0 4. A grafikon a logaritmikus függvény mindig áthalad a ponton (1; 0). 5. A növekvő logaritmikus függvény, pozitív x> 1, és negatív 0<х<1. Az alábbi ábrán egy grafikon csökkenő logaritmikus függvény - (0 7. A funkció nem páros vagy páratlan. Logaritmikus függvény - függvényében a kinézetét. 8. A függvény maximális és minimális pontot. FIELD meghatározó Rvseh funkció- a valós számok halmazán. A beállított függvény értékei - az intervallum [-1; 1], azaz szinuszfüggvényt - korlátozott. Páratlan funkció: sin (-x) = - sin x minden x ∈ R. függvény grafikonját szimmetrikus a eredetű. A periodikus függvény a legkisebb pozitív periódus 2π. sin (x + 2π · k) = sin x, ahol k ∈ Z, minden x ∈ R. sin x = 0 x = π · k. k ∈ Z. sin x> 0 (pozitív) minden x ∈ (2π · k. π + 2π · k), k ∈ Z. sin x <0 (отрицательная) для всех x ∈ (π+2π·k. 2π+2π·k ), k ∈ Z. A funkció növeli -1-től 1 időközönként: Funkció csökken -1-től 1 időközönként: 21)) A számok halmaza, amelyek mindegyike el van látva saját számát n (n = 1, 2, 3), az úgynevezett egy numerikus szekvenciát. Külön számok a szekvenciában nevezzük tagjai, amelyet általában a következők szerint: Az első ciklus A1. második a2. n-edik ciklus egy, és így tovább. d. Minden számszerű sorrendben feltüntetett 22) számtani sorozat. Numerikus szekvencia, minden egyes tagja, amely, kezdve a második, az egyenlő az előző egymásra egy konstans számú erre szekvencia d, nevezzük egy számtani sorozat. A szám d a különbség a progresszió. Bármely tagja egy számtani sorozat a következőképpen számítjuk ki: A összege az első n feltételei egy számtani sorozat kiszámítani: Mértani. Numerikus szekvencia, minden egyes tagja, amely, kezdve a második, azonos az előzővel, szorozva az állandó erre sorszám q. Ez az úgynevezett geometriai progresszióját. A szám q hívják a nevező progresszió. Bármely tagja egy mértani a következőképpen számítjuk ki: A összege az első n elemének egy mértani kiszámítani: Végtelen mértani a végtelen mértani amelynek nevező megfelel. Határtalan összegét növelik az első tagja a végtelen mértani hajlamos a számot. amely nazyvaetsyasummoy végtelen mértani. ) Függvény deriváltját f (x), f „(x). maga is függvénye. Ennélfogva, lehetséges, hogy megtalálják EO proizvodnuyu.Nazovom f „(x) differenciálhányados f (x) az első poryadka.Proizvodnaya származékot f (x) nevezzük másodrendű származékot (vagy második derivált). Geometriai értelmében a származék. A származék x pontban 0 egyenlő a lejtőn a érintő a függvény grafikonját y = f (x) ezen a ponton. Az egyenlet az érintő a függvény grafikonját: y = f (a) + F '(a) (x - a) Y = f (a) + F' (a) (x - a) A fizikai értelmében a származék. Ha a pont mozog az x tengely mentén, és koordináta változik a törvény szerint az x (t) a pillanatnyi sebesség a lényeg: 24)) származéka az összeg (különbség) függvények A származék algebrai összege funkciók fejezzük ki a következő tétel. Származék összeg (különbség) két differenciálható függvények összegével egyenlő (különbség) ilyen származék funkciók: Származtatott véges algebrai összege differenciálható függvények azonos algebrai összege származékok feltételeket. Például,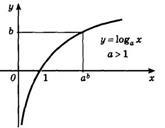
Kapcsolódó cikkek