Magic constant - ez
Varázslat. vagy magic square - egy négyzet asztal tele n 2 számokat úgy, hogy a számok összege minden sorban, minden oszlopban és a két átlója egyforma. Ha a négyzet számok összege egyenlő csak a sorok és oszlopok, ez az úgynevezett semimagic. Normál nevezzük mágikus négyzet, tele egész szám 1-től n 2. A Magic Quadrant nevezik asszociatív vagy szimmetrikus. ha az összeg bármely két egész szám, szimmetrikusan elrendezett viszonyítva a tér közepén egyenlő 2 n + 1.
Normál mágikus négyzetek létezik minden megrendelések, kivéve a n = 2. Bár az ügy n = 1 triviális - a tér áll egy számot. Minimális triviális esetben az alábbiakban mutatjuk be, ez a rend 3.
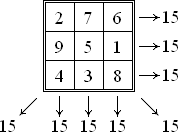
A számok összege minden sorban, oszlopban és átlósan az úgynevezett mágikus állandó. M. magic constant szokásos bűvös négyzet csak attól függ, n, és adja
Az első érték mágikus konstansok vannak adva az alábbi táblázatban (sorrendben A006003 OEIS-ben):
Számok összege bármilyen vízszintes, függőleges és átlós egyenlő 34. Ez az összeg is megtalálható minden a négyzet sarkainak 2 × 2 egy központi tér (10 + 11 + 6 + 7), a tér a sarok sejtek (16 + 13 + 4 + 1 ) a négyzetek épített "swing ló" (2 + 8 + 9 + 15 és a 3 + 5 + 12 + 14), a téglalapok által alkotott pár szekunder cellák ellentétes oldalain (3 + 2 + 15 + 14 és 5 + 8 + 9 + 12). A legtöbb kiegészítő szimmetriák kapcsolódó tény, hogy az összeg a bármely két központilag szimmetrikus elrendezésű szám egyenlő 17.
Négyzetek Henry E. Dudeney és Allan W. Johnson ml.
Ha egy négyzetes mátrix n × n van rögzítve nem szigorúan természetes számok, akkor a mágikus négyzet - nem konvencionális. Az alábbiakban két ilyen mágikus négyzetek töltött többnyire prímszám. Az első a rend n = 3 (Dudeney négyzet); második (méret 4x4) - Johnson téren. Mindkettőt alakult ki a huszadik század elején [6]:
Számos ilyen példát:
Az utolsó téren, 1913-ban épült Dzh.N.Mansi, figyelemre méltó, hogy ez áll a 143 egymást követő prímszám, kivéve két dolgot: a résztvevő egység, ami nem prímszám, és nem csak használják páros prímszám 2.
Négyzetek további tulajdonságokkal
Ördög bűvös négyzet
Ördög bűvös négyzet - mágikus négyzet, ami szintén egybeesik a magic constant számok összege törött átlós (diagonális, ami azáltal kerültek kialakításra a tér torr) mindkét irányban.
A négyzetek nevezzük inkább pandiagonalnymi.
Vannak ördögi mágikus négyzetek 48 4 × 4-ig forgatások és gondolatokkal. Ha figyelembe vesszük egyre szimmetria - tórikus párhuzamos fordítás, akkor lesz csak 3 jelentősen eltérő tér:
Építő mágikus négyzetek
Még könnyebb elvégezni az építkezés a következő. Kezdődik mátrix n x n. Belül épül lépés gyémánt. Ebben a cellában balra fel az átlók töltik egymást követő páratlan számok. Meghatározott értéke, a központi cella C. Ezután, a mágikus négyzet sarkait értékek a következők: jobb felső cella C-1; Alsó bal oldali cella C + 1; jobb alsó cella C-n; bal felső cella C + n. Üres celláinak kitöltése lépésben szögek a háromszögek megfelelően elvégzett egyszerű szabályok: 1) a sorok száma, balról jobbra növekvő lépésekben n + 1; 2) oszlopok a tetejétől az aljáig a növekvő lépés száma az n-1.
algoritmusok építésére pandiagonalnyh terek, [14] [15] is, és pandiagonalnyh és asszociatív 9x9 bűvös négyzetek is kifejlesztettek. [16] [17] Ezek az eredmények lehetővé teszik, hogy építeni az ideális mágikus négyzetek rend n = 9 (2k + 1). [9] [18] Van is egy közös módszer ideális elrendezését mágikus négyzetek a páratlan rendű n> 3 [19] Eljárás építésének ideális mágikus négyzetek rend n = 8k, k = 1,2,3. [20] Pandiagonalnye négyzetek páros-páratlan érdekében tudja összekapcsolni csak akkor, ha nem szokványos. [21] [22] [23]. Azonban lehet találni szinte pandiagonalnye négyzetek [24] Van egy speciális csoport ideálisan tökéletes mágikus négyzetek (hagyományos és nem hagyományos) [25].
Példák a bonyolultabb négyzetek
Szigorúan módszeresen dolgozott mágikus négyzetek páratlan rendű és az, hogy a kettős paritás. [26] A formalizálása négyzetek rend egyetlen paritás nehezebb, hogy illusztráljuk a következő séma szerint:
Több tucat más módszerek felépítésének mágikus négyzetek
Chess megközelítés
Köztudott, hogy a sakk. mágikus négyzetek, több tucat évszázaddal ezelőtt Indiában. Ezért nem véletlen, hogy az ötlet a lépcsőzetes megközelítés az építési mágikus négyzetek. Ez az első alkalom ez az ötlet fejezte ki Euler. Megpróbált a teljes mágikus négyzet folyamatos bypass ló. Ahhoz azonban, hogy ezt nem sikerült, mert a fő átlóinak a számok összege eltér a mágikus állandó. Mindazonáltal sakk bontás lehetővé teszi, hogy bármilyen mágikus négyzet. A számok töltik rendszeresen, és figyelembe véve a sorban a sejtek színe.
A fényképek áramkörök építésére mágikus négyzetek.