A binomiális tétel és Pascal háromszöget, a tudomány és az élet
A binomiális tétel és Pascal háromszöget

Blaise Pascal (1623- 1662).

Isaac Newton (1643-1727).
Tény, hogy nincs semmi félni. Binomiális tétel - általános képletű tetszőleges természetes bomlás mértékét binomiális \ ((a + b) ^ n \) egy polinom. Mindannyiunknak fejből tudja formula „négyzet összege» \ ((a + b) ^ 2 \) és a „kocka összege» \ ((a + b) ^ 3 \), de növeli a kitevő az együtthatók megállapításához a feltételeket a polinom Start nehézségeket. Annak érdekében, hogy ne hibázik, és a binomiális tétel vonatkozik:
Egy még általánosabb formában, képletű binomiális együtthatók írható:
ahol k - sorszáma a kifejezés polinom.
Emlékezzünk, hogy a faktoriális - a termék természetes számok 1-től n, akkor \ (1 * 2 * 3 * \ ldots * n \) - jelöljük N!, Például \ (4 = 1 * 2 * 3 * 4 = 24! \).
Ne feledje, a képlet nagyon egyszerű. De megpróbáljuk elemezni. Nyilvánvaló, hogy bármelyik polinom tartalmaz N és B n együtthatók 1. Az is világos, hogy bármely más tagja a polinom néz ki, mint a termék egy bizonyos fokú minden egyes kifejezés a binomiális (A + B), sőt az összege az fok mindig egyenlő n-nel. Például, a kifejezés \ [(a + b) ^ 3 = a ^ 3 + 3a ^ 2b + 3ab ^ 2 + b ^ 3 \] összege fok a tényezők minden tekintetben megegyeznek az három (3, 2 + 1, 1 + 2, 3). Ugyanez igaz minden más mértékben. A kérdés csak az, milyen tényezőket kell tenni a tagállamok számára.
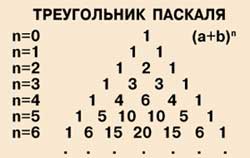
Úgy tűnik, annak érdekében, hogy megkönnyítse a munkáját a tudósok és diákok, a nagy francia matematikus és fizikus Blaise Pascal háromszázötven éve feltalált egy speciális eszköz azonosítására a legtöbb ilyen tényező - „Pascal háromszöget”.
Ez a következőképpen van felépítve obrazom.V háromszög csúcsa olvasó egység 1 felel meg az expressziós \ ((a + b) ^ 0, \), mert tetszőleges számú hatványát nulla, ad egységet. Építő kiegészítések alatti háromszög írok többet a készüléket. Ez hôtágulása azonos binomiális emeljük az első fok: \ (. (A + b) ^ 1 = a + b \) lépés előre. oldalán a háromszög képző egységek közötti, valamint - az összeg két is, hogy a tetején, azaz a 2. Ez a háromtagú együtthatók „tér sum”:
A következő sorozat, valamint az előző, kezdődik és végződik az egységek közötti, valamint - az összeg a számok, amelyek felett: 1, 3, 3, 1 Megvan az együtthatók összege kocka „bomlás. Számos binomiális együtthatók negyedik hatványával lesz 1, 4, 6, 4, 1, és így tovább.
Például segítségével Pascal háromszög bővült polinom összege binomials a hatodik fokozat:
\ [(A + b) ^ 6 = a ^ 6 + 6a ^ 5b + 15a ^ 4b ^ 2 + 20a ^ 3b ^ 3 + 15a ^ 2b ^ 4 + 6AB ^ 5 + b ^ 6. \]
Minden nagyon egyszerű, és emlékezett egy életen át. By the way, a saját, és ne feledje, hogy a binomiális képlet, támaszkodva a tervezet a Pascal háromszög is sokkal könnyebb.