Numerikus optimalizálás matlab
Szia, kedves olvasók. Továbbra is foglalkozunk a Matlab. Ma a téma kapcsolódik a numerikus optimalizálás - a megállapítás a helyi és globális szélsőérték funkcióinak egy vagy több változó a Matlab környezetben.
áttekintés
Tehát, ebben a blokkban semmit Matlab nem csak a koncepció optimalizálás. Ez a koncepció csökken a szempontjából a minimális és maximális funkciót, vagy a rövid - szélsőséges.
Alatt egy minimális értéket funkció érteni, hogy néhány szomszédságában ez a függvény a legkisebb érték az összes lehetséges értéket ezen a környéken. Ennek megfelelően, a legnagyobb - a legnagyobb érték a függvény minden környéken.
Ha nem érti - ez egy egyszerű példát, hogy minden ismert parabola:
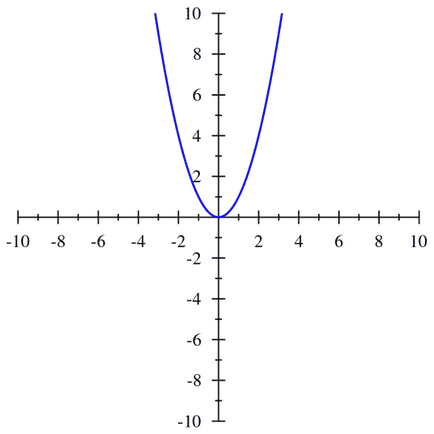
Ez a funkció egy minimális, és ez azon a ponton x = 0. Ez a pont az úgynevezett minimális pontot, és az értéke ennek a funkciónak a minimális (ez is egyenlő 0). Maximumokat ez a funkció nem áll fenn, de ha a függvény fejjel lefelé, úgy tűnik.
Gyakran vannak olyan összetett feladatokat, amelyek több és minimumok és maximumok. És ebben az esetben, ossza meg a fogalmakat a helyi és globális szélsőértékek. Helyi - a szélsőséges érték, amelyet az határoz meg egy bizonyos régióban, és a globális - az egész tartomány a funkciót. A fenti ábrán a globális minimum a parabola.
Keresés szélsőértékek Matlabban
És most, ha legalább olyan találkozott a fogalmak optimalizálása és megtalálása szélsőérték funkciók, akkor folytassa a megállapítás maximumok és minimumok Matlabban. Továbbá, mivel a szokásos fogjuk elemezni példákat különböző összetettségű. A példák tartalmazzák a standard Matlab parancsok megtalálása a minimális és maximális a funkció, és a másik rész - végrehajtási módszer a semmiből.
Szabványos módszerei Matlab
Nézzük meg a problémát találni minimum 2 Matlab:
1. példa. Számítsuk ki a függvény minimuma f (x) = - x 1 / x. grafikusan határoztuk intervallum lokalizáció. Számításának rendelkeznek egy minimális lépés a argumentum 1 * 10 -5
Először hozzon létre egy script, ami kijelzi a szolgáltatás. Itt a kód, hogy:
Fuss a forgatókönyvet, és kap:
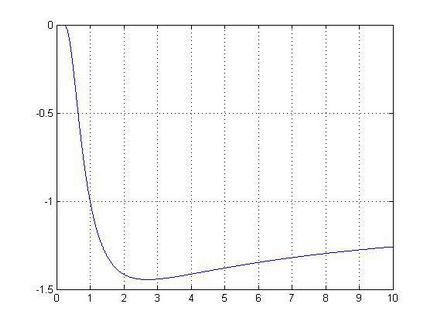
Szerint a függvény grafikonját, arra a következtetésre jutunk, hogy van legalább egy, és annak koordinátái tartományban 2,5-3, hogy van, akkor csökkenti a keresési intervallum minimális.
Most hozzon létre egy másik forgatókönyvet, adja meg a nevét és first.m írja elő azt funkció:
Így ebben m-file meghatároztuk a funkciót. Most, a parancs ablakban írunk elő az alábbi kódot:
És megkapjuk a következő értékeket:
x = 2,7183 - minimális koordináta pont
y = -1,4447 - legkisebb érték
Ebben a részben a kód szoktuk Matlab szabványos módszert találni a minimális függvényében - fminbnd. átadjuk 3 paraméter - a funkciót is, és a szünetekben minimum keresést. Meg kell jegyezni, hogy ez a módszer csak alkalmas egyváltozós függvényeket.
Tehát, ez a probléma, létrehoztunk 2 script fájlt, hogy lehet letölteni a végén a cikk.
2. példa. Számítsuk ki a minimális funkciója két változó x 4 + y 4 2 -2x + 4xy-2y 2 +1 pontossággal 1 * 10-5.
Koordinátáit a kiindulási pont a keresési [1,0 -1.0].
Kezdeni, megépíteni a grafikon két változó - ez létre fog hozni egy új forgatókönyvet, és előírják, ahol ezt a kódot:
surf funkció lehetővé teszi, hogy építsenek egy háromdimenziós grafika és megjeleníti a mélység értékek jobb megértését. Futtatni a szkriptet - a végén kiderült ütemezés szerint:
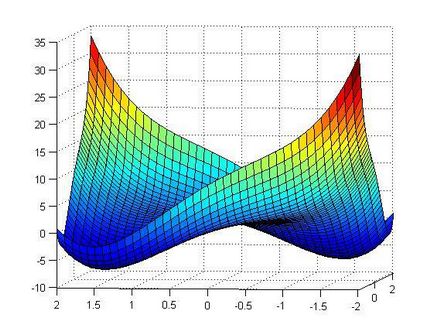
Ahogy a grafikonon látható, van két terület, ahol van egy helyi minimum (sötétkék területek), és a célunk az, hogy megtaláljuk a koordinátákat, és értékeit a két pontot. Az általunk használt szabványos Matlab eszközöket, és hozzon létre egy új szkriptet nevű second.m, ahol és előírhatja a kódot:
Ezt követően, a parancssorból, valamint az első probléma, felírni standard funkció Matlab:
Kapjuk az alábbi következtetést:
Ahhoz, hogy megtalálja a minimális Matlab, ezúttal használni a funkciót fminsearch. Ez a funkció valósítja simplex - Nelder-Mead módszer. A kimenet akkor több változót z koordináták beiratkozott minimum pontot f értéke ezzel a minimum. És exitflag változók és kiadási feltöltött feltételek megszakíthatja a keresési folyamatot, és információkat az optimalizálás, ill.
Ennek eredményeként ismét fordult 2 m-fájlt.
Newton módszer Matlab
Most próbálja meg végrehajtani Newton-módszert, hogy optimalizálja a funkciót.
3. példa. Newton módszert találni a minimális pont x, * és a minimális értéke az f függvény * f (x) = (X-2) 4 -lnx xє intervallum [2, 3] C pontossággal 10 -7
Kezdjük azzal, hogy hozzunk létre egy új szkriptet, és nevezd el Newton.m. Ezután írja elő azt kód:
Elég világos funkció, amely együttműködik az első és a második derivált a szimbolikus funkció, amely úgy, mint a paraméter. Szintén elfogadta a választási lehetőségeket. Ez a függvény az a pont koordinátáit és értékét a szélsőérték.
Most hogy ezt a funkciót a parancs ablakban:
Az eredmény a következő volt:
Xk = 2,4663
Yk = -0,8554
Nem fogjuk adni a menetrend, de akkor nézd meg magad, hogy a mért értékeket helyesen. Fontos, hogy azt mondják, hogy ez a módszer csak talál egy helyi szélsőérték, és ha a kiválasztott tartományban több szélsőérték, akkor a módszer nem találja az egyik, amire szüksége van.
Szintén fontos, hogy megkérdezze, hogyan lehet szűkíteni a keresési tartományban, különben a módszer nem működik megfelelően, különösen akkor nyilvánul periodikus függvények a típus cos (x), stb
következtetés
Nos, ebben a cikkben megnéztük néhány módszert találni szélsőérték Matlabban. Mi használjuk a szokásos módszerekkel, és bevezette a Newton módszer Matlab környezetben. Forrásaik alább.
letöltés forrás