A tömegközéppont síkidom
A törvény szerint az egyetemes tömegvonzás valamennyi szerv vonzódnak a földet egy erő arányos testtömeg (m - test tömege és g = 9,81 m / s 2), ez az erő az úgynevezett testtömeg (gravitáció).
Ha figyelembe vesszük az egyensúlyt és a mozgás komplex alakú testek fontos tudni, hogy a helyzet a súlypont a test.
Tekintsük helyzetének meghatározására a súlypontja az anyag AVV1 A1 lemezt egy íves trapéz által határolt felső görbe AB. amely adott kifejezetten a y = y (x). és vonalak x = a. X = b (a
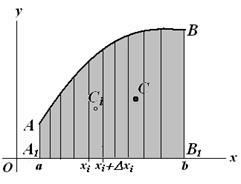
Tegyük fel, hogy a felületi sűrűsége a lemez anyagának állandó, azaz a ábra homogén. Feltételezhető az meghatározottsága, hogy az arány a lemez anyag 1 ( # 947; = # 961; g = 1, # 961; - az anyag sűrűsége), míg a tömeg a lemez vagy annak része bármely alkalmas területen.
Ahhoz, hogy meghatározza a helyzetét a súlypont tart a figyelembe vett térelválasztó lemez a függőleges rudak bázisok i = 1,2, ..., n (). A súlypont az egyes sávok által meghatározott koordinátákat
és ahol - a pontok koordinátáinak a görbe (= y ()).
A tömegközéppont tekinthető AVV1 A1 homogén lemez. valamint bármely más, a test, az a tulajdonsága, hogy a helyzete nem függ a forgatás a lemez bármilyen szögben képest a függőleges. Amint az az elméleti mechanika a súlypont koordináták által meghatározott képletek
ha a partíciók száma végtelenhez közelít, és a hossza a válaszfal elemek. A képletek (7,15) - a terület i - edik partíció szalag
Figyelembe a határérték képletekben (7,15), és mikor. megfelelő összegeket elválaszthatatlan, azonban a görbe vonalú koordinátáit a súlypontja trapéz által meghatározott képletek
Notes. 1. Ha a síkidom a tengelye vagy központ szimmetria, a súlypont a figura a tengelyen vagy központ szimmetria.
2. Ha a test áll részek, amelyek a súlypontok ismertek, akkor a súlypont a vegyület alakja határozza meg a képletek
Itt k - a komponensek száma; Si és xi. yi - rendre a területet és a koordinátáit a súlypont i-edik rész. Ha a síkidom lyukak, a súlypont az ábra által meghatározott azonos képlet, de a megfelelő területet a furat negatívnak kell lennie.
Példa. Határozza meg a súlypontja negyedkörben koordinátái (x, y> 0). Nézzük képviseli ezt síkidom
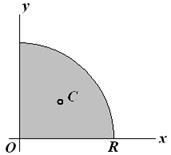
Terület negyedbe.
Határozza meg a szerves számlálója (7,16) (ezek integrálok nevezzük statikus pillanatok)
Ezek a koordináták a súlypontja a negyedben vannak