Összefoglaló másodrendű görbék ellipszis, kör, parabola, hiperbola

Szövetségi Oktatási Ügynökség az Orosz Föderáció

Állami oktatási felsőoktatási intézmény a Dél-Ural Állami Egyetemen.

Az osztály „Commodity és vizsgálata fogyasztási cikk”

„Curves másodrendű: ellipszis, kör, parabola, hiperbola”

A fegyelem a magasabb matematika.

Permina Alexandra Nikolaevna

diákcsoport 131

Kravchenko Olga

Curves másodrendű ellipszis, kör, parabola, hiperbola.

Másodrendű görbék a síkban nevezzük a vonal metszi a kúpos síkokkal való áthaladás nélkül a csúcsa.

Ha egy ilyen sík metszi az összes üreget a kúp, a részén egy ellipszis kapunk. a kereszteződésekben a két alkotó üregek - hiperbola. és ha a keresztmetszet síkja párhuzamos a generátort, a keresztmetszete a kúp egy parabola.

A másodrendű görbe egy síkban egy derékszögű koordináta-rendszer által leírt egyenlettel:

A készlet minden pontot a síkon, amelyek a távolságok összege a két fix pont F 1 és F 2 egy előre meghatározott állandó értéket, az úgynevezett ellipszis.

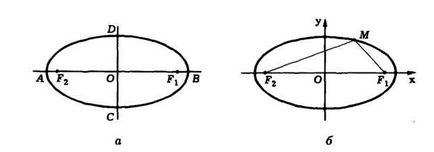
Canonical egyenlet egy ellipszis.

Bármely ellipszis megtalálható derékszögű koordináta rendszerben, hogy a ellipszis egyenletben leírt (kanonikus egyenlete az ellipszis):

Leírja ellipszis origó középpontú, amelyek tengelyei egybeesnek a koordinátatengelyek. A szám egy úgynevezett fő tengelye az ellipszis. száma és a b - a kisebb tengely.

• Focal tulajdon. Ha F1 és F2 - gócok az ellipszis, majd minden egyes pont X, tartozik egy ellipszis, közötti szög az érintő ezen a ponton, és egy egyenes vonal (F1X) egyenlő a szög az érintő és a vonal (F2X).
• Egy egyenes át húzott közepén a szegmensek lehet levágni a két párhuzamos vonal metszi az ellipszis mindig áthalad a közepén az ellipszis. Ez lehetővé teszi, hogy az építkezés egy vonalzó és iránytű könnyű megszerezni az ellipszis központja, később tengely felső és trükköket.
• Evolután az ellipszis astroid.
• A excentricitása az ellipszis az aránya. A excentricitás jellemzi az ellipszis. Az excentricitás közel nulla, az ellipszis több, mint egy kör, és fordítva, a különcség közelebb van, annál nyújtva.

Ellipszis is leírható, mint

• ez a szám lehet beszerezni a kör alkalmazásával egy affin transzformáció
• ortogonális vetülete a kör a gépen.
• A metszéspontja a sík és körkörös henger.

Kerület - plane pontok helye egyenlő távolságra egy adott ponton, az úgynevezett közepén egy előre meghatározott, nem nulla távolság, az úgynevezett sugara.

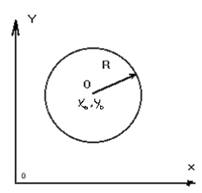
A kanonikus egyenlete egy kört.

Az általános egyenlet a kör van írva, mint:

Point - a kör középpontját, R - a sugara.

A kör egyenlete R sugarú középpontú eredetű:

• Direkt nem lehet közös pont a kör; Ez egy kerülete egy közös pont (tangens); Van két közös pontja (metsző) vele.
• A kör érintője mindig merőleges az átmérőjével, amelynek egyik vége az a pont érintési.
• Három pont, hogy nem fekszenek egy egyenes vonal, akkor rajzoljon egy kört, és akkor is csak egy.
• az érintési pont a két kör fekszik összekötő vonal a központokban.
• A kerülete egy R sugarú lehet a következő képlettel számítjuk C = 2π R.
• Vagy kerületi szög egyenlő fele a központi által bezárt szög az ív His vagy komplementer felét ez a szög 180 °.
  • Két kerületi szög alapján ugyanazon ív egyenlő.
  • Egy kerületi szög által bezárt az ív hossza fél kerülete 90 ° -kal egyenlő.
• A szög két egymást metsző levont pontokat kívül eső kerülete félmegoldásokkal ívek között fekvő disszonáns.
• A szög a metsző akkordokat felével egyenlő az ív akció fekvő szöget ív és előtte.
• A bezárt szög tangense és az akkord felével egyenlő az ív által bezárt a húrt.
• A szegmensek kör érintőjén lefolytatott egyik pontról egyenlő, és hogy az egyenlő szöget zárnak be a vonal áthalad ezen a ponton, és a közepén a kör.
• A kereszteződés két akkordok a termék szegmensek, amelyek osztják egyik metszéspont, a termék a többi szegmens.
• A terméket a hossza a távolságok a kiválasztott pontot a két metszéspontja a kör és a szekáns áthaladó kiválasztott pont nem függ a szelő és egyenlő abszolút értékeinek erejét egy pont.
  A tér szegmense hossza megegyezik a termék az érintő a szegmensek hossza, és metsző abszolút értéke erejét egy pont.
• A kör egy egyszerű sík másodrendű görbe.
• Kerületének egy kúpszelet ellipszis és privát rendezvény.

A parabola a pontok halmaza a síkban, amelyek mindegyike egyenlő távolságra egy adott pont, úgynevezett fókusz, és az adott vonalon, úgynevezett direktrix és áthalad a hangsúly.

Canonical egyenlete parabola egy derékszögű koordináta-rendszert:

(Vagy ha a tengely változtatni helyeken)

ahol p (fokális paraméter) - távolság a fókuszt direktrixét

• Parabola - görbe másodrendű.
• Ez egy szimmetriatengelye, az úgynevezett tengelye a parabola. A tengely átnyúlik a fókuszt és merőleges a direktrix.
• A fénysugár a tengellyel párhuzamosan, tükröződik egy parabola, ez fog koncentrálni. Egy parabola a vertex a koordináta (0, 0), és a pozitív iránya az ágak a fókuszpont a ponton (0, 0,25).
• Ha a hangsúly a parabola tükrözik a relatív érintője, akkor annak képe lesz az igazgatónő.
• Parabola negatív pedál görbe egy egyenes vonal.
• Minden parabola hasonlóak. Ez határozza meg a távolságot a fókusz és a zoom direktrixszel.
• Ha forog a szimmetria tengelye a parabola kapunk elliptikus paraboloid.

· A vonal metszi a parabola nem több, mint két pontot.

· Az excentricitást egy parabola e = 1.

A pontok helye a síkban, ahol a különbség a távolságot két fix pont állandó hívják hiperbola.

Bármely túlzó talál egy Descartes úgy, hogy túlzó leírása a következő egyenlet:

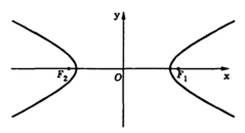
A számok hívják, illetve a valós és képzetes tengelyének túlzás.

· Hiperbola két szimmetriatengelye (a fő tengelye a hiperbola) és a központ a szimmetria (középen hiperbola). Így az egyik tengely metszi a hiperbola két ponton, az úgynevezett csúcs hiperbola. Ezt nevezik a valós tengelyének a hiperbola (x tengely a kanonikus választott koordinátarendszer). Egyéb tengely nem metszik a hiperbola és az úgynevezett képzeletbeli tengelye (a kanonikus koordináták - y tengely). Mindkét oldalán úgy vannak elrendezve, jobb és bal oldali ága egy hiperbola. A gócok a hiperbola található tényleges tengelyen.

· Minden túlzás egy pár aszimptotákkal és.

· Távolsága a származási egyik fókusz a hiperbola nevezzük gyújtótávolság a hiperbola.

· Excentricitás hiperbola az a mennyiség, e = c / a. A excentricitása a hiperbola e> 1

· Távolsága a csúcsa a hiperbola aszimptóta a párhuzamos irányban függőleges tengelyen az úgynevezett kis vagy képzetes tengelyének hiperbola.

· A távolság a hangsúly a túlzó párhuzamos vonal mentén az y tengely az úgynevezett fokális paraméter ..