Differenciálegyenletek mozgás egy pont - studopediya
Révén differenciálegyenletek megoldott második feladat dinamikáját. Szabályzat elkészítése ezen egyenletek függ, hogy milyen módon akarjuk határozni a mozgását egy pont.
1) meghatározása a koordináta mozgás pont módszer.
Tekintsük a szabad anyagi pont alatt mozgó erők .. Draw rögzített tengelyek Oxyz (4. ábra). Pro-ektiruya mindkét oldalról a tengelyek, és figyelembe véve, hogy stb kapjunk differenciálegyenletek, görbe pályájú mozgás-zheniya pont kiemelkedések a tengely a derékszögű Descartes-féle koordináta-rendszer:
Mivel a ható erő egy pont függhet az idő és a pont pozícióját a sebesség, akkor a jobb oldalán egyenletek tartalmazhatják a t idő, a pont koordinátái x, y, z és a vetülete a sebessége. A jobb oldali egyes egyenlet tartalmazza az összes ezeket a változókat.
Ahhoz, hogy használni ezeket az egyenleteket megoldani az alapvető problémát a dinamika, szükség van, amellett, hogy a fellépő erőket, hogy ismerjük a kezdeti feltételeket, azaz a helyzetét és sebességét egy pont a kezdeti időben. A koordináta-tengelyek Oxyz kezdeti feltételek adottak formájában: ha
Ismerve a tényleges erők integrálását követően az egyenletek találjuk a koordinátái x, y, z, a mozgó pont, mint a t idő függvényében, azaz Találunk a törvény a mozgás egy pont.
3. példa Tanulmány mozgás test dobni a kezdeti sebesség szögben a vízszintes, figyelembe véve, mint egy anyagi pont m tömegű. Ez elhanyagolása az ellenállást a levegő és a gravitációs tér feltételezi egységes (F = const), feltételezve, hogy a repülési távolság és pályája magassága kicsi a Föld sugara.
Helyezzük a származási O a kiinduló helyzetbe pontot. Mi irányítjuk a tengely függőlegesen felfelé; vízszintes tengely Ox egy síkban áthaladó vektor Oy. és töltik a Oz tengelye merőleges az első két tengely (5. ábra). Ezután közötti szög a vektor és a tengely Ox egyenlő.
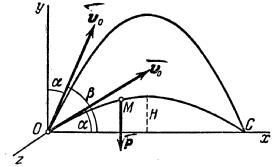
Azt mutatja, mozgó pontra M bárhol az úton. Azon a ponton, egyedül a gravitáció. ahol a nyúlványok a koordinátatengely. . .
Behelyettesítve ezeket az értékeket differenciálegyenletek és megjegyezve, hogy stb kapjuk az alábbi csökkentését m:
Megszorozzuk mindkét oldalán az egyenlet által dt és integrálása, azt találjuk:
A kezdeti feltételek a probléma az alábbi formájú:
Kielégíti a kezdeti feltételek, van:
Behelyettesítve ezeket az értékeket C1. C2 és C3 oldatban felett található és cseréje. megérkezik az egyenleteket:
Integrálása ezeket az egyenleteket, megkapjuk:
Behelyettesítve a kezdeti adatok ad C4 = C5 = C6 = 0, és végül megtalálják az egyenlet a mozgás a M pont formájában:
Az utolsó egyenlet következik, hogy a mozgás a síkban Oxy.
Az egyenlet a mozgás kinematikai pont módszerekkel lehet meghatározni minden jellemzőjével ezt a mozgást.
1. Az útvonal a lényeg. Kivéve az első két egyenletet (1) t idő, megkapjuk az egyenlet egy pálya pont:
Ez - az egyenlet a parabola tengelyével párhuzamos Oy tengellyel. Így, dobott szögben a horizonton nehéz pont mozog egy vákuumkemencében mentén parabola (Galileo).
2. A vízszintes távolság. Határozza meg a vízszintes távolság, azaz a mentén mért Ox tengely távolsága OC = X. Elhelyezés egyenlet (2) y = 0, azt találjuk, a metszéspont a pálya az X-tengelyen. Az egyenlet:
Az első megoldás ad pont O. második pont C. Következésképpen, X = X2 és végül
Tól (3) világos, hogy ugyanabban a vízszintes X távolságot kapjuk szögben. e. azaz ha a szög. Következésképpen, egy adott kezdeti sebesség egy és ugyanazon C pont érhető el két út: on-elegáns () és a csuklós ().
Amikor egy előre meghatározott kezdeti sebessége maximális vízszintes tartományban vákuum akkor kapunk, ha. azaz szögben.
3. A magasság a pályáját. Ha fel a (2) egyenlet
. akkor ott van a magassága a pálya H:
4. A repülési idő. Az első (1) egyenlet azt jelenti, hogy a teljes repülési idő T határozza meg az egyenletet. Cseréje X értékét, megkapjuk
Maximális hatótávolság szög, melyek mind-soraiban vannak:
Az eredmények szinte teljesen alkalmazható irányítható, héj tirovochnogo meghatározó repülési jellemzőit (rakéta), amelynek 200 ... 600 km, hiszen ezek a távolságok (és) a nagy része a lövedék útját kiterjed a sztratoszférában, ahol a levegő ellenállása lehet figyelmen kívül hagyni. Kisebb távolságok az eredmény nagyban befolyásolni fogja-Vezetékellenállás a levegő, és egy sor, több mint 600 km gravitációs nem tekinthető állandó.
4. példa A pisztolyt telepített h magasságban. Kirúgták szögben a vízszintes (6.). A mag levette a fegyver csövét a sebesség u. Mi határozza meg a kernel az egyenlet a mozgás.
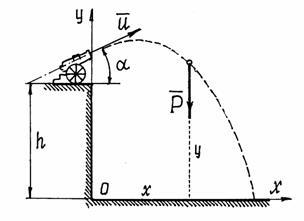
Annak érdekében, hogy dolgozzon ki egy differenciálegyenlet a mozgás, meg kell megoldani az ilyen problémákat egy adott áramkört.
a) hozzárendelése a koordináta-rendszer (a tengelyek száma és azok irányának eredetű). Sikeresen kiválasztott tengely egyszerűsítése döntést.
b) ábra egy pont egy közbenső helyzetben. Meg kell róla, hogy a koordináták egy ilyen rendelkezés szükségszerűen pozitív (6. ábra).
B) ábra ható erők egy pont a köztes helyzet (tehetetlenségi erők nem mutatnak!).
Ebben a példában - csak a hatalom. kernel súlyát. Légellenállás nem kell figyelembe venni.
d) létrehozása a differenciálegyenletek a képletek. Így megkapjuk két egyenlet: és.
d) Oldjuk meg a differenciálegyenlet.
Itt kapott egyenlet - másodrendű lineáris egyenletek, a jobb oldalon - állandó. A megoldás az egyenletek elemi.
Továbbra is megtalálják az integrációs állandók. Behelyettesítve a kezdeti feltételeket (t = 0 az x = 0, y = h ,.) A négy egyenlet :. . C2 = 0. h = D2.
Mi helyettesíti az értékek állandók az egyenlet, és írjon a mozgásegyenletek egy pont a végleges formáját
Ezekkel egyenletek, amint ez ismert a kinematika szakaszban lehet meghatározni, és a mozgáspályája a mag, és a sebesség és a gyorsulás, és helyzetét a mag bármely adott időpontban.
Mint látható ebből a példából, problémamegoldó rendszer igen egyszerű. Nehézségek csak merülnek fel a megoldás, differenciálegyenletek, amely lehet nehéz.
2) Annak meghatározása, hogy a természetes módon.
Koordinátor módszer általában határozza meg a mozgás a pont, nem korlátozódik semmilyen körülmények között, kötvények. Ha a mozgás a ponton korlátozta a sebességet vagy a pozíció meghatározásához mozgás koordináta út nem könnyű. Sokkal kényelmesebb használni a természetes módszer megadásával mozgás.
Határozza meg, például mozgása egy előre meghatározott pont a vezetékes, előre meghatározott úton (ábra. 7).
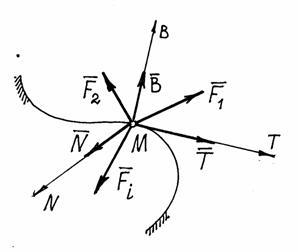
A M pont, kivéve, ha kifejezetten az aktív erők. jár reakció vonalat. Megmutatjuk a komponensek a reakció a természetes tengelyek
Mi alkotják az alapvető egyenlet a dinamika és a projekt azt a természetes tengelyen
Mivel megkapjuk a differenciálegyenletek a mozgás, pl
Itt az erő - a súrlódási erő. Ha a vonal, amelyen a pont mozog, sima, akkor T = 0, majd a második egyenlet csak egyetlen ismeretlen - koordináta s:
-Egyenlet, megkapjuk a törvény a mozgás egy pont. ezért ha szükséges, és a sebesség és a gyorsulás. Az első és a harmadik egyenlet (5), és lehetővé teszi a reakció, hogy megtalálja.