A középérték-tétel Lagrange
Lagrange véges lépésekben képletű
Lagrange véges lépésekben képletű kifejezi a viszonyát a növekmény az egyes folytonos intervallumon [a; b] és differenciálható az intervallum (a; b) egy függvény y = f (x) és az értéke annak származéka: ahol c - számos intervallumban (a; b): a A geometriai jelentése Lagrange képlet a következő: az ív keletkezett ez a funkció a pontokat összekötő (a, f (a)) és a (b, f (b)), van egy pont (a, f (c)) (és esetleg több) amelyben az érintő a függvény grafikonját párhuzamos a húrt végeket köti össze az ív - ld ..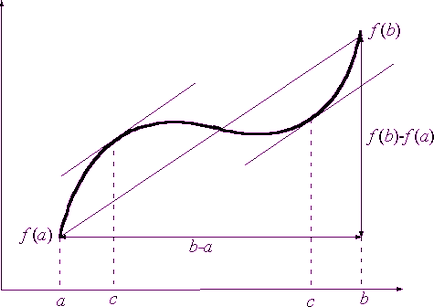
Lagrange-féle képlet gyakran írják más, ezzel egyenértékű formában: ahol Θ - ismeretlen számú függő, általában véve, a x0 és Ah és kielégítő 0<Θ <1.
Lagrange-formula funkciók több változó a következő: ahol 0<Θ <1.
A Lagrange-féle képlet lehet bizonyítani a következőképpen annak általánosítása - Cauchy középérték-tétel: Ha az f és g függvények folytonosak intervallumon [a; b] és differenciálható az intervallum (a; b), ahol a g „(x) ≠ 0 (a, b), akkor az intervallum (a; b) van egy pont c. ez viszont, ez a tétel megkönnyíti bizonyítani az egyik legfontosabb arányok az elmélet határait - L'Hospital-szabály.