Aktív mechanizmusokat a parazita kerekek

Magán mechanizmust, ahol mindegyik közbenső fogaskerék egy független forgástengelye és összekapcsolódik két szomszédos nevezett közönséges átviteli parazita kerekek (ábra. 5).

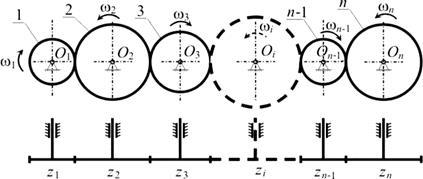
Ábra. 5. Rendes átviteli parazita kerekek

A áttétel a fogaskerekek a következőképpen határozzuk meg:

ahol k - a szám a külső hivatkozások a mechanizmus.

A kapott értéket áttétel nem függ a fogainak száma közbülső kerekekkel. Ezért ezek a kerekek úgynevezett parazita. Ezek, anélkül, hogy az érték az áttétel, befolyásolja annak jele, azaz a A forgásirány az utolsó hajtott elem.

Általában normál adatátviteli a parazita kerekek használt a forgatás a hajtott tengely sebességváltó egy bizonyos irányba (gépi sebességváltó, autó, stb), valamint annak biztosítása érdekében, a sebességváltó a mozgás, a nagy távolságokat, és a kis értékei sebességfokozatok ha lehetetlen, hogy növelje a méret a vezető és a hajtott kerekeket.

Aktív mechanizmusok többszörös terhelés

Magán mechanizmus, ahol a közbülső kerekekkel van páronként közös forgástengelye és vegyen egy szomszédos kerék nevezett közönséges mechanizmus többszörös terhelés (ábra. 6.).

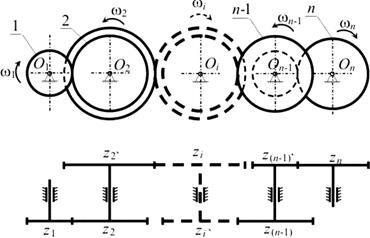
Ábra. 6. Rendes átvitel többszörös terhelés

A fogaskerék áttétel úgy definiáljuk, mint:

ahol k - a számos külső hivatkozások; ; .

Így az érték az áttétel rendes átviteli többszörös áttétel termékek arányának a fogainak száma a meghajtott kerekek az elemi fogazat, hogy a termék a számai a meghajtott kerekek.

Aktív részvétel olyan mechanizmusokat, amelyek több alkalmazott, hogy nagy áttételek.

Megjegyzés. A szöghajtás (ábra. 7), a jele áttétel által meghatározott nyilak szabály jellemző forgási irányát kerekek. Minden egyes pár kapcsolódó kerekek nyilak mutatnak egymás elemét azonos nevet (vagy csücsök vagy írás).

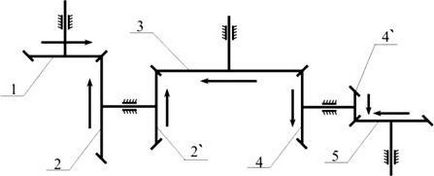
Ábra. 7. kúpkerekek

A rendszer az ábra. A 7. ábra ezt a szabályt:

A „-” jel a i1-5 kiválasztott miatt többirányú nyilak a bemeneti és kimeneti a transzfer.

Bolygókerekes hajtómű

Fogaskerekek, amelyek kerekek mozgó mértani tengelyek úgynevezett bolygószerű.

Kerék mozgó tengelyek, úgynevezett műholdak. részt két forgatást: a saját tengelye körül, és vele egy rögzített tengely. A mozgatható elem, ahol a tengely a műholdak kerülnek nevezik a hordozó (pórázon). Ez a kapcsolat a diagramok betűvel jelölt H.

A kerekek, amelyek helyhez tengely, és amelyre a tekercs műholdak úgynevezett központi. Általában planetáris mechanizmusok készülnek koaxiális.

Planetary mechanizmusok vannak osztva eltérés és bolygókerekek.

Differenciálművet vagy eltérés az úgynevezett bolygómű, amelyben a központi forognak. Differentials használják kombinálva két mozgásainak vezetŒszemei ​​a slave kapcsolat vagy bővítése mozgását a meghajtó elem a hajtott mozgását két független egység.

A rendszer egyszerű differenciálművet ábrán látható. 8.

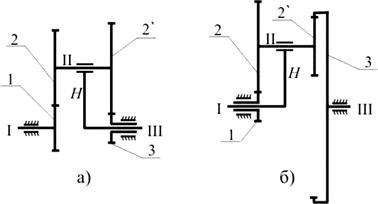
Ábra. 8. A legegyszerűbb eltérés átviteli

A központi kerekek 1 és 3 körül forognak elhelyezkedő tengelyekkel kollineáris szögsebessége W1 és w3. H WH hordozóval körül forog közös geometriai tengelye az 1 kerék és a 3. műholdak 2-2` szerelt csapágy hordozót H és végre komplex mozgás: a saját tengelye körül, és együtt egy tengely körül H III ábrán. 8, hanem a tengely körül ábrán az I. 8b (transzlációs mozgás).

Az fokú mobilitás mechanizmusok vonatkozóan:

Ie eltérés kell két meghajtó egység, mint például egységek 1 és H. Ezután, a szögsebesség egységek a 2. és 3. kerül meghatározásra.

Annak megállapítására, az áttétel alapuló eltérés átviteli módszerrel állapították fordított mozgás. Ebből a célból, az összes hivatkozást a mechanizmus jelentett további forgási szögsebességgel (-WH). Ennek eredményeként, a hordozó helyhez kötött és kiderül egy közönséges átvitel, amely meghatározható a áttétel a képletek (2) és (3).

Például, az áramkör ábrán. 8 és kap egy táblázatot:

A kezdeti szögsebessége linket

Ezért egy olyan mechanizmust a fordított

ahol - a fogaskerék aránya a mechanizmus szemben egy rögzített ketrecben H.

Általában, hogy megkapjuk az N kerekek Willis képletű:

Willis képlet meghatározására használt szögsebessége műholdak. Erre a célra a műhold látható folytat a központi kerék, ami szögsebesség ismert. Például, ábrával. 8 és